Cho 2 đường tròn O và O' cắt nhau tại A và B. Qua A vẽ cát tuyến CAD (C∈ (O), D∈ (O') ). Từ C và D vẽ 2 tiếp tuyến với 2 đường tròn, 2 tiếp tuyến này cắt nhau tại E
CMinh tứ giác BCED nội tiếp được 1 đường tròn

Những câu hỏi liên quan
Cho 2 đường tròn O và O' cắt nhau tại A và B. Qua A vẽ cát tuyến CAD (C∈ (O), D∈ (O') ). Từ C và D vẽ 2 tiếp tuyến với 2 đường tròn, 2 tiếp tuyến này cắt nhau tại E
CMinh tứ giác BCED nội tiếp được 1 đường tròn
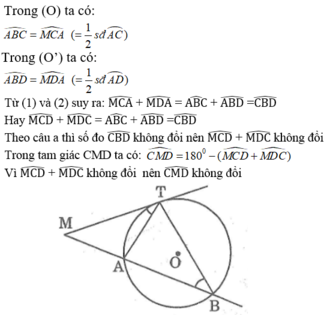
Hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai đường tròn (C ∈ (O) ,D ∈ (O’)). Từ C và D vẽ hai tiếp tuyến với đường tròn.Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến CAD quay xung quanh điểm A
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn tâm (O). Từ B và C vẽ hai tiếp tuyến của đường tròn, hai tiếp tuyến này cắt nhau ở D. Qua D vẽ một cát tuyến sonng song với AB, cát tuyến này cắt đường tròn tại các điểm M và N và cắt cạnh AC tai I
a) Chứng minh tứ giác OBDC nội tiếp đường tròn (O)
b) Chứng minh I là trung điểm của dây MN
1. Cho đường tròn ( O) và đường thẳng xy nằm ngoài đường tròn. Từ O kẻ OA vuông góc với xy. Qua A vẽ cát tuyến cắt đường tròn (O) ở B và C. Tiếp tuyến với đường tròn (O) tại B và C cắt xy ở D và E. Chứng minh: A là trung điểm của DE2. Cho tứ giác ABCD có AB BD nội tiếp đường tròn (O) . Từ A vẽ tiếp tuyến với đường tròn (O) cắt đường thẳng BC ở Q , gọi R là giao điểm của AB và CD. Chứng minh: a) tứ giác AQRC nội tiếp được 1 đường tròn b) QR//AD
Đọc tiếp
1. Cho đường tròn ( O) và đường thẳng xy nằm ngoài đường tròn. Từ O kẻ OA vuông góc với xy. Qua A vẽ cát tuyến cắt đường tròn (O) ở B và C. Tiếp tuyến với đường tròn (O) tại B và C cắt xy ở D và E. Chứng minh: A là trung điểm của DE
2. Cho tứ giác ABCD có AB = BD nội tiếp đường tròn (O) . Từ A vẽ tiếp tuyến với đường tròn (O) cắt đường thẳng BC ở Q , gọi R là giao điểm của AB và CD. Chứng minh:
a) tứ giác AQRC nội tiếp được 1 đường tròn
b) QR//AD
Ta có: tỨ giác OCEA nội tiếp
=> \(\widehat{OCA}=\widehat{OEA}\)(1)
Vì OC=OB
=> Tam giác OBC cân
=> \(\widehat{OCA}=\widehat{OCB}=\widehat{OBC}\)(2)
Tứ giác ODAB nội tiếp
=> \(\widehat{ODA}=\widehat{OBC}\)( cùng bù với góc OBA) (3)
Từ (1), (2), (3)
=> \(\widehat{ODA}=\widehat{OEA}\)
=> Tam giác ODE cân có OA là đươngcao
=> OA là đường trung tuyến
=> A là trung điểm của DE
Đúng 0
Bình luận (0)
Cho 2 đường tròn (O) và (O') cắt nhau tại A và B(O và O' nằm khác phía vs AB).Qua A kẻ cát tuyến cắt đường tròn (O) ở C.Cắt (O') ở D.Các tiếp tuyến của 2 đường tròn kẻ từ C và D,cắt nhau ở I.Chứng minh rằng khi cát tuyến CAD thay đổi thì:
a)Góc CBD ko đổi
b)Góc CID ko đổi
*Bài 1: Hai đường tròn (O) và (O) cắt nhau tại A và B. Đường thẳng qua A cắt đường tròn (O) tại điểm C và cắt đường tròn (O) tại điểm Da) Chứng minh khi đường thẳng quay quanh A thì widehat{CBD}có sđ không đổib) Từ C và D vẽ 2 tiếp tuyến với đường tròn. CMR góc tạo bởi 2 tiếp tuyến này có số đo không đổi khi cát tuyến CAD quay quanh A*Bài 2: Từ điểm M ở ngoài đường tròn (O), kẻ tiếp tuyến MT (T là tiếp điểm) và cát tuyến MAB qua O ( A,Binđường tròn, A ở giữa M và D). CM: widehat{AMT}+widehat{MT...
Đọc tiếp
*Bài 1: Hai đường tròn (O) và (O') cắt nhau tại A và B. Đường thẳng qua A cắt đường tròn (O) tại điểm C và cắt đường tròn (O') tại điểm D
a) Chứng minh khi đường thẳng quay quanh A thì \(\widehat{CBD}\)có sđ không đổi
b) Từ C và D vẽ 2 tiếp tuyến với đường tròn. CMR góc tạo bởi 2 tiếp tuyến này có số đo không đổi khi cát tuyến CAD quay quanh A
*Bài 2: Từ điểm M ở ngoài đường tròn (O), kẻ tiếp tuyến MT (T là tiếp điểm) và cát tuyến MAB qua O ( A,B\(\in\)đường tròn, A ở giữa M và D). CM: \(\widehat{AMT}+\widehat{MTA}=90^o\)
Từ điếm A ở ngoài đường tròn (O;R) vẽ các tiếp tuyến AB,AC đến (O) với B,C là các tiếp điểma/ Chứng minh OA vuông góc BC tại H và tứ giác OBAC nội tiếp đường trònb/ Từ A vẽ cát tuyến ADE (không qua O) cắt (O) tại D và E (D nằm giữa A và E). Chứng minh: AD.AE AB2c/ Vẽ dây cung BM song song với DE. Gọi giao điểm của CM và DE là i. Chứng minh i trung điểm DEmọi người giúp mik với ạ
Đọc tiếp
Từ điếm A ở ngoài đường tròn (O;R) vẽ các tiếp tuyến AB,AC đến (O) với B,C là các tiếp điểm
a/ Chứng minh OA vuông góc BC tại H và tứ giác OBAC nội tiếp đường tròn
b/ Từ A vẽ cát tuyến ADE (không qua O) cắt (O) tại D và E (D nằm giữa A và E). Chứng minh: AD.AE= AB2
c/ Vẽ dây cung BM song song với DE. Gọi giao điểm của CM và DE là i. Chứng minh i trung điểm DE
mọi người giúp mik với ạ
a) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
hay OA⊥BC(đpcm)
Đúng 1
Bình luận (0)
Cho điểm A nằm ngoài đường tròn (O;R). Vẽ các tiếp tuyến AB, AC với đường tròn (O) tại B và C.
a) CM: tứ giác ABOC nội tiếp được đường tròn
b) Vẽ cát tuyến ADE với đường tròn (O), cát tuyến ADE không qua tâm O; D nằm giữa A và E ). CM: AB^2=AD.AE=OA^2-R^2
c) Gọi H là giao điểm của BC và OA. Cm: tứ giác HDEO nội tiếp
Cho đường tròn (O) và đường thẳng xy không cắt (O). Vẽ OA vuông góc với xy tại A. Qua A vẽ 1 cát tuyến bất kỳ cắt (O) tại B và C (B nằm giữa A và C). Tiếp tuyến tại B và C của (O) cắt xy tại D và E. Chứng minh:
a) Tứ giác OBAD nội tiếp
b) góc ODB = góc OEC
c) AE = AD
a:góc OAD=góc OBD=90 độ
=>OBAD nội tiếp
b: góc EAO+góc ECO=180 độ
=>ECOA nội tiếp
=>góc OEC=góc OAC=góc ODB
Đúng 0
Bình luận (0)