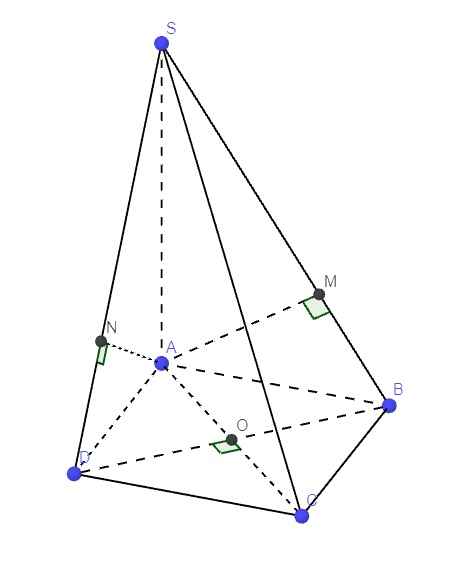
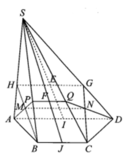
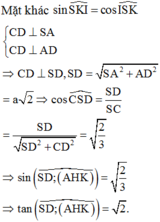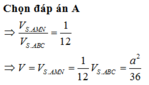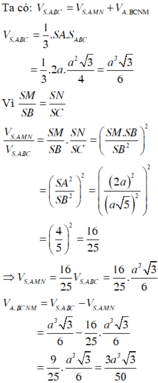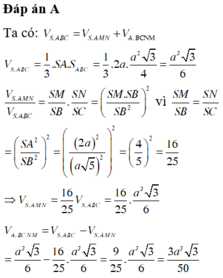cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, cạnh bên SA vuông góc với đáy và SA=3a.Gọi M,N lần lượt là hình chiếu của A trên SB,SD.Tính chu vi tam giác AMN.

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, cạnh bên SA vuông góc với đáy và SA=3a. Gọi M,N lần lượt là hình chiếu của A trên SB,SD.
a, Cmr: SC vuông góc với mpAMN
b, Tính chu vi tam giác AMN
Mn giải giúp em với ạ
a.
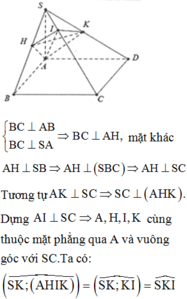
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\)
Mà \(AM\perp SB\)
\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\) (1)
Hoàn toàn tương tự, ta có \(AN\perp\left(SCD\right)\Rightarrow AN\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(AMN\right)\)
b.
\(SB=SD=\sqrt{SA^2+AB^2}=a\sqrt{13}\)
Áp dụng hệ thức lượng trong tam giác vuông SAB:
\(AM=\dfrac{SA.AB}{SB}=\dfrac{6a\sqrt{13}}{13}\)
Hệ thức lượng tam giác vuông SAD:
\(AN=\dfrac{SA.AD}{SD}=\dfrac{6a\sqrt{13}}{13}\)
\(\Rightarrow AM=AN\Rightarrow SM=SN=\sqrt{SA^2-AM^2}=\dfrac{9a\sqrt{13}}{13}\)
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{SN}{SD}\Rightarrow MN||BD\Rightarrow\dfrac{MN}{BD}=\dfrac{SM}{SB}\)
\(\Rightarrow MN=\dfrac{SM.BD}{SB}=\dfrac{18a\sqrt{2}}{13}\)
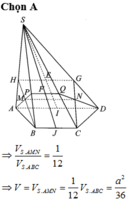
\(\Rightarrow AM+AN+MN=...\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy SA
a
2
. Gọi M, N lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SD (tham khảo hình vẽ). Góc giữa mặt phẳng (AMN) và đường thẳng SB bằng A. 45
°
B. 60
°
C. 90
°
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy SA = a 2 . Gọi M, N lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SD (tham khảo hình vẽ). Góc giữa mặt phẳng (AMN) và đường thẳng SB bằng
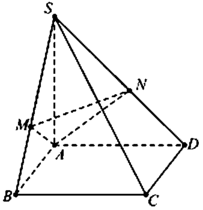
A. 45 °
B. 60 °
C. 90 °
Đáp án B
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .
Đúng 0
Bình luận (1)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA 2a. Gọi B’, D’ lần lượt là hình chiếu vuông góc của A trên các cạnh SB, SD. Mặt phẳng (AB’D’) cắt cạnh SC tại C’. Tính thể tích của khối chóp S.AB’C’D’. A.
a
3
3
B.
16
a
3
45
C.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA = 2a. Gọi B’, D’ lần lượt là hình chiếu vuông góc của A trên các cạnh SB, SD. Mặt phẳng (AB’D’) cắt cạnh SC tại C’. Tính thể tích của khối chóp S.AB’C’D’.
A. a 3 3
B. 16 a 3 45
C. a 3 2
D. a 3 2 2
Đáp án B.
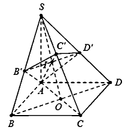
Gọi O là tâm của hình vuông ABCD, nối S O ∩ B ' D ' = I .
Và nối AI cát SC tại C’ suy ra mp (AB’D’) cắt SC tại C’.
Tam giác SAC vuông tại A, có S C 2 = S A 2 + A C 2 = 6 a 2 ⇒ S C = a 6 .
Ta có B C ⊥ S A B ⇒ B C ⊥ A B ' và S B ⊥ A B ' ⇒ A B ' ⊥ S C .
Tương tự A D ' ⊥ S C suy ra S C ⊥ ( A B ' D ' ) ≡ ( A B ' C ' D ' ) ⇒ S C ⊥ A C ' .
Mà S C ' . S C = S A 2 ⇒ S C ' S C = S A 2 S C 2 = 2 3 và S B ' S B = S A 2 S B 2 = 4 5 .
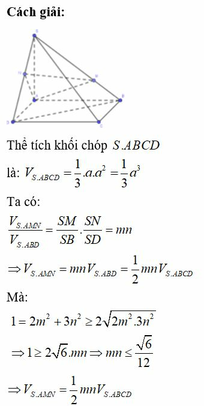
Do đó V S . A B ' C ' = 8 15 V S . A B C = 8 30 V S . A B C D mà V S . A B C D = 1 3 . S A . S A B C D = 2 a 3 3 .
Vậy thể tích cần tính là V S . A B ' C ' D ' = 2 . V S . A B ' C ' = 16 a 3 45
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, cạnh bên SA vuông góc với mặt phẳng đáy và SAa.Gọi H, K lần lượt là hình chiếu vuông góc của A trên SB, SD (tham khảo hình vẽ bên). Tang của góc tạo bởi đường thẳng SD và mặt phẳng (AHK) bằng A.
3
B.
2
C.
1
3
D.
3
2
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, cạnh bên SA vuông góc với mặt phẳng đáy và SA=a.Gọi H, K lần lượt là hình chiếu vuông góc của A trên SB, SD (tham khảo hình vẽ bên). Tang của góc tạo bởi đường thẳng SD và mặt phẳng (AHK) bằng
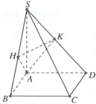
A. 3
B. 2
C. 1 3
D. 3 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, ABa, BC2a. Cạnh bên SA vuông góc với đáy và SAa. Gọi M, N lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích V của khối chóp S.AMN A.
V
a
3
36
B.
V
a
3
5
15
C.
V...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a, BC=2a. Cạnh bên SA vuông góc với đáy và SA=a. Gọi M, N lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích V của khối chóp S.AMN
A. V = a 3 36
B. V = a 3 5 15
C. V = a 3 3 18
D. V = a 3 30
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
A
B
a
,
B
C
2
a
.Cạnh bên SA vuông góc với đáy và SAa. Gọi M, N lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích V của khối chóp S.AMN.
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = a , B C = 2 a .Cạnh bên SA vuông góc với đáy và SA=a. Gọi M, N lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích V của khối chóp S.AMN.
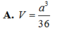
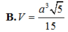

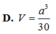
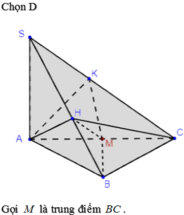
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông cân tại B, BC2a, cạnh bên SA vuông góc với đáy. Gọi H, K lần lượt là hình chiếu của A lên SB và SC, khi đó thể tích của khối cầu ngoại tiếp hình chóp AHKCB là
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông cân tại B, BC=2a, cạnh bên SA vuông góc với đáy. Gọi H, K lần lượt là hình chiếu của A lên SB và SC, khi đó thể tích của khối cầu ngoại tiếp hình chóp AHKCB là
![]()
![]()
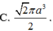
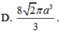
Cho hình chóp S.ABCD có đáy BACD là hình vuông cạnh a, cạnh bên SA a và vuông góc với mặt đáy (ABCD). Trên SB, SD lần lượt lấy hai điểm M, N sao cho
S
M
S
B
m
0
,
S
N
S
D
n
0
.
Tính thể tích lớn nhất...
Đọc tiếp
Cho hình chóp S.ABCD có đáy BACD là hình vuông cạnh a, cạnh bên SA = a và vuông góc với mặt đáy (ABCD). Trên SB, SD lần lượt lấy hai điểm M, N sao cho S M S B = m > 0 , S N S D = n > 0 . Tính thể tích lớn nhất V max của khối chóp S,AMN biết 2 m 2 + 3 n 2 = 1 .
A. V max = a 3 6 72
B. V max = a 3 48
C. V max = a 3 3 24
D. V max = a 3 6
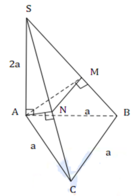
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA 2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng A.
V
3
a
3
3
50
B.
V...
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng
A. V = 3 a 3 3 50
B. V = 9 a 3 3 50
C. V = 8 a 3 3 75
D. V = 8 a 3 3 25
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA 2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng A.
V
3
a
3
3
50
B.
V
9...
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng
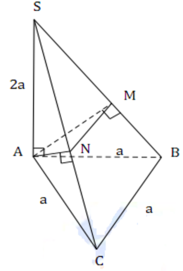
A. V = 3 a 3 3 50
B. V = 9 a 3 3 50
C. V = 8 a 3 3 75
D. V = 8 a 3 3 25