tìm số nguyên k sao cho 36n-1-k.33n-2+1 chia hết cho 7 với mọi số nguyên dương n.
MN GIÚP MIK VS NHANH NHANH NHA
Tìm số nguyên k sao cho 36n-1 - k . 33n-2 + 1 chia hết cho 7 với mọi số nguyên dương n
Ta thấy :
36n-1 - k . 33n-2 + 1 ⋮ 7 <=> 9 . ( 36n-1 - k . 33n-2 + 1 ) ⋮ 7
<=> 36n+1 - k . 33n + 9 ⋮ 7
Vì 36n+1 ≡ 3 ( mod 7 ) , suy ra 36n+1 + 9 ≡ 5 ( mod 7 )
Do đó để 36n+1 - k . 3 + 9 ⋮ 7 thì k . 33n ≡ 5 ( mod 7 )
Từ đó ta chứng minh được : Nếu n chẵn thì k ≡ 5 ( mod 7 ) , còn nếu n lẻ thì k ≡ -5 ( mod 7 )
tìm số nguyên X (X khác -1) sao cho 2 x X chia hết cho X + 1
nhanh giúp mik với
Tìm các số nguyên dương n lẻ sao cho n-1 là số nguyên dương nhỏ nhất trong các số nguyên dương k thỏa mãn \(\frac{k\left(k+1\right)}{2}\)chia hết cho n
Cho S = k2 + k + 1 .
a, Chứng minh rằng S không chia hết cho 9 với mọi số nguyên k.
b,Nếu k là số nguyên dương, thi S có thể là số chính phương không? Vì sao?
Với mọi số nguyên dương n≥3 và mọi số nguyên dương k, chứng minh rằng:
n k không chia hết cho n-1.
n k -1 chia hết cho n-1
Thử ha! Lâu không làm quên mất cách làm rồi má ơi:((
Giả sử \(n^k⋮n-1\left(1\right)\Rightarrow n⋮n-1\) Vì:
Nếu n không chia hết cho n - 1 thì khi phân tích ra thừa số nguyên tố, n không chứa n - 1 nên nk cũng không chưa thừa số nguyên tố n - 1 suy ra nk không chia hết cho n - 1. Mâu thuẫn với điều giả sử (1)
Vậy \(n⋮n-1\Leftrightarrow\left(n-1\right)+1⋮\left(n-1\right)\Rightarrow1⋮\left(n-1\right)\)
Suy ra \(n-1\inƯ\left(1\right)=1\left(\text{không xét }-1\text{ vì n\ge3 nên }n-1\text{dương. Do vậy ta chỉ xét ước dương}\right)\Rightarrow n=2\)
Mà n = 2 không thỏa mãn đk nên không tồn tại n > 3 thỏa mãn n chia hết cho n - 1 tức là không tồn tại nk chia hết cho n - 1 (mẫu thuẩn với điều giả sử)
Do vậy ta có đpcm.
P/s: Sai thì thôi nhá, quên mất cách làm mọe rồi
nk-1=(n-1)(nk-1-nk-2....+1) chia hết cho n-1
Chứng minh với mọi số nguyên \(n\)thì \(n^3\left(n^2-7\right)^2-36n\)chia hết cho 7
GIÚP MIK VỚI
Ta có : \(n^3\left(n^2-7\right)^2-36n\)
\(=n[\left(n^3-7n\right)^2-36]\)
\(=n\left(n^3-7n-6\right)\left(n^3-7n+6\right)\)
\(=n[\left(n-3\right)\left(n^2+3n+2\right)][\left(n+3\right)\left(n^2-3n+2\right)]\)
\(=n\left(n-3\right)\left(n+1\right)\left(n+2\right)\left(n+3\right)\left(n-1\right)\left(n-2\right)\)
là tích của 7 số nguyên liên tiếp
\(\Rightarrow n\left(n-3\right)\left(n+1\right)\left(n+2\right)\left(n+3\right)\left(n-1\right)\left(n-2\right)⋮7\)
hay \(n^3\left(n^2-7\right)^2-36n⋮7\forall n\inℤ\)
làm giúp mik bài này nhé. Ai nhanh mik tích
Tìm các số nguyên sao cho 5n+1 chia hết cho n-2
bn vào link này nha :
https://olm.vn/hoi-dap/question/313346.html
5n+1 chia hết cho n-2
=> (5n-10)+10+1 chia hết cho n-2
=> (5.n-5.2)+11 chia hết cho n-2
=> 5.(n-2)+11 chia hết cho n-2
có n-2 chia hết cho n-2 => 5.(n-2) chia hết cho n-2
=> 11 chia hết cho n-2
=> n-2 thuộc Ư(11)
đến đây bạn tự lập bảng là Ok!
:)
\(5n+1⋮n-2\)
ta có \(n-2⋮n-2\)
\(\Rightarrow5\left(n-2\right)⋮n-2\)
\(\Rightarrow5n-10⋮n-2\)
mà \(5n+1⋮n-2\)
\(\Rightarrow5n+1-\left(10n-10\right)⋮n-2\)
\(\Rightarrow5n+1-10n+10\) \(⋮n-2\)
\(\Rightarrow11\) \(⋮n-2\)
\(\Rightarrow n-2\in\text{Ư}_{\left(11\right)}=\text{ }\left\{1;-1;11;-11\right\}\)
+) nếu \(n-2=1\Rightarrow n=3\) ( thỏa mãn )
+) nếu \(n-2=-1\Rightarrow n=1\) ( thỏa mãn )
+) nếu \(n-2=11\Rightarrow n=13\) ( thỏa mãn )
+) nếu \(n-2=-11\Rightarrow n=-9\) ( thỏa mãn )
vậy \(n\in\text{ }\left\{3;1;13;-9\right\}\)
Cho dãy số ( a n ) thỏa mãn 5 a n + 1 - a n = 3 3 n + 2 với mọi n ≥ 1. Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên.
A. n = 41
B. n = 39
C. n = 49
D. n = 123
Chọn A
Với số tự nhiên n ≥ 1, ta có:
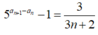
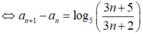
![]()
Suy ra:
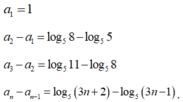
Cộng tương ứng hai vế các đẳng thức trên ta có ![]() với mọi số tự nhiên n
≥
1
với mọi số tự nhiên n
≥
1
Để ![]()
![]()
Ta kiểm tra với các giá trị k ∈ ℕ từ bé đến lớn
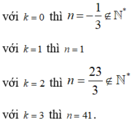
Vậy số nguyên n > 1 nhỏ nhất là n = 41( ứng với k = 3).
Cho p là số nguyên tố. Tìm tất cả các số nguyên k sao cho \(\sqrt{k^2-pk}\) là số nguyên dương. Giúp mik với
ĐK \(k\left(k-p\right)\ge0\)
Để \(\sqrt{k^2-pk}\)là số nguyên
=> \(k\left(k-p\right)\)là số chính phương
Gọi UCLN của k và k-p là d
=> \(\hept{\begin{cases}k⋮d\\k-p⋮d\end{cases}}\)
=> \(p⋮d\)
Mà p là số nguyên tố
=> \(\orbr{\begin{cases}p=d\\d=1\end{cases}}\)
+ \(p=d\)=> \(k⋮p\)=> \(k=xp\left(x\in Z\right)\)
=> \(xp\left(xp-p\right)=p^2x\left(x-1\right)\)là số chính phương
=> \(x\left(x-1\right)\)là số chính phương
Mà \(x\left(x-1\right)\)là tích của 2 số nguyên liên tiếp
=> \(\orbr{\begin{cases}x=0\\x=1\end{cases}\Rightarrow}\orbr{\begin{cases}k=0\\k=p\end{cases}}\)
+\(d=1\)
=>\(\hept{\begin{cases}k=a^2\\k-p=b^2\end{cases}\left(a>b\right)}\)
=> \(p=\left(a-b\right)\left(a+b\right)\)
=> \(\hept{\begin{cases}a+b=p\\a-b=1\end{cases}}\)=> \(\hept{\begin{cases}a=\frac{p+1}{2}\\b=\frac{p-1}{2}\end{cases}}\)
=> \(k=\frac{\left(p+1\right)^2}{4}\)với p lẻ
Vậy \(k=0\)hoặc k=p hoặc \(k=\frac{\left(p+1\right)^2}{4}\forall plẻ\)
\(\sqrt{k^2-pk}\) là số nguyên dương => \(k^2-pk>0\Rightarrow k>p\)
Khang chú ý là sẽ không xảy ra k=0 hoặc k=p nhé!
vâng,em cảm ơn , Em không để ý đề bài cho là nguyên dương