Đáp án C

Ta có: Δ ' = ( - 2 ) 2 - 1 . ( m + 1 ) = 3 - m

Để phương trình đã cho có nghiệm thì Δ '   =   3   -   m   ≥   0   ⇔   m   ≤   3 .

Với điều kiện trên thì phương trình đã cho có 2 nghiệm x 1 ; x 2 .

Theo hệ thức Vi-et ta có:  x 1 . x 2  = m + 1

Để  x 1 x 1 . x 2  = 4 thì m + 1 = 4 nên m = 3 ( thỏa mãn điều kiện)

Đáp án D

* Với m = -1 thì phương trình đã cho trở thành: 4x + 1 = 0  ⇔ x = -1/4

Do đó, m = -1 thỏa mãn điều kiện.

* Nếu m  ≠ -1 , khi đó phương trình đã cho là phương trình bậc hai một ẩn.

Ta có:  △ =  4 2 - 4.(m + 1).1 = 16 - 4m - 4 = 12 - 4m

Để phương trình đã cho có nghiệm khi:  △ = 12 - 4m  ≥ 0

-4m  ≥  - 12 ⇔ m ⩽  3

Kết hợp 2 trường hợp, để phương trình đã cho có nghiệm thì m  ⩽ 3.

\(\Delta=b^2-4ac=4^2-4m\)

Để pt có 2 nghiệm \(x_1,x_2\) thì \(\Delta\ge0\Rightarrow16-4m\ge0\Rightarrow m\le4\)

Theo Vi-ét, ta có :

\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{b}{a}=4\\x_1x_2=-\dfrac{c}{a}=-m\end{matrix}\right.\)

Ta có : \(x_1^2+x_2^2=10\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)

\(\Leftrightarrow4^2-2.\left(-m\right)=10\)

\(\Leftrightarrow16+2m=10\)

\(\Leftrightarrow m=-3\)

Đáp án D

* Xét phương trình : x 2 – 4 x + 4 = 0

⇔ ( x - 2 ) 2 = 0 ⇔ x - 2 = 0 ⇔ x = 2

Vậy phương trình này có nghiệm duy nhất.

Để hai phương trình đã cho có nghiệm chung khi và chỉ khi x = 2 là nghiệm phương trình

x 2 + ( m + 1 ) x + m = 0 .Suy ra:

2 2 + ( m + 1 ) . 2 + m = 0

⇔ 4 + 2m + 2 + m = 0 ⇔ 6 + 3m = 0

⇔ 3m = -6 ⇔ m = -2

a.

Phương trình có 2 nghiệm khi:

\(\Delta'=4-2m\ge0\Rightarrow m\le2\)

b.

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=2m\end{matrix}\right.\)

\(x_1^2+x_2^2-x_1-x_2=16\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)=16\)

\(\Leftrightarrow16-4m-4=16\)

\(\Leftrightarrow m=-1\) (thỏa mãn)

a.\(\Delta=\left(-4\right)^2-4.2m=16-8m\)

Để pt có nghiệm x1, x2 thì \(\Delta>0\)

\(\Leftrightarrow16-8m>0\)

\(\Leftrightarrow-8m>-16\)

\(\Leftrightarrow m< 2\)

b.

Theo hệ thức Vi-ét, ta có:\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1.x_2=2m\end{matrix}\right.\)

\(x_1^2+x_2^2-x_1-x_2=16\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2-\left(x_1+x_2\right)=16\)

\(\Leftrightarrow4^2-2.2m-4-16=0\)

\(\Leftrightarrow-4m-4=0\)

\(\Leftrightarrow m=-1\)

Đáp án D

Ta có:

Δ ' = ( - 2 ) 2 - 1 . ( 2 m - 2 ) = 2 - 2 m

Để phương trình đã cho có hai nghiệm dương phân biệt khi và chỉ khi:

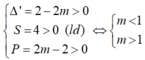
Suy ra không có giá trị nào của m thỏa mãn

c) tim x₁ và x₂ theo ct; 

x₁= 16 +can denta ....tu lam

d) c/a <0

lam dc roi chu 

a) Ta có: \(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(2m-3\right)=16-4\left(2m-3\right)\)

\(\Leftrightarrow\Delta=16-8m+12=-8m+28\)

Để phương trình có hai nghiệm x1;x2 phân biệt thì \(-8m+28>0\)

\(\Leftrightarrow-8m>-28\)

hay \(m< \dfrac{7}{2}\)

Với \(m< \dfrac{7}{2}\) thì phương trình có hai nghiệm phân biệt x1;x2

nên Áp dụng hệ thức Viet, ta có: 

\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-4\right)}{1}=4\\x_1\cdot x_2=\dfrac{2m-3}{1}=2m-3\end{matrix}\right.\)

Để phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau thì 

\(\left\{{}\begin{matrix}m< \dfrac{7}{2}\\4+2m-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\m=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{2}\)

Vậy: Khi \(m=-\dfrac{1}{2}\) thì phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau