Tính diện tích tam giác ABC biết AB = 3cm , AC = 5 cm , trung tuyến AM = 2 cm

Những câu hỏi liên quan
Cho tam giác ABC, AB= 3cm , AC= 5cm, trung tuyến AM = 2 cm. Tính diện tích tam giác ABC.
diện tích tam giác là 3.5=15(cm )thế nha bạn dễ ọt yk
d
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
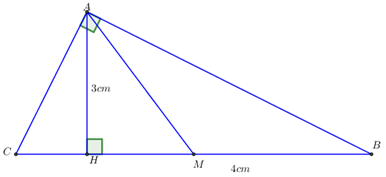
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM .Biết AH = 3cm, HB = 4 cm. Hãy tính AB AC AM , và diện tích tam giác ABC .
Xét tam giác ABH vuông tại H, ta có:
\(AB^2=AH^2+BH^2\)\(=3^2+4^2=25\)
\(\Rightarrow AB=5\left(cm\right)\)
Xét tam giác ABC vuông tại A, theo hệ thức lượng ta có:
\(AH^2=AB\cdot AC\Rightarrow AC=\dfrac{AH^2}{AB}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
Do đó:\(BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+1,8^2}\simeq5,3\left(cm\right)\)
AM là đường trung tuyến trong tam giác vuông ABC
=> AM=\(\dfrac{1}{2}\) BC= 2,65 \(\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM .Biết AH = 3cm, HB = 4 cm. Hãy tính AB AC AM , và diện tích tam giác ABC .
Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5 cm. Kẻ các đường phân giác AD, trung tuyến AM (M, D thuộc cạnh BC). Tính diện tích tam giác ADM.
Kẻ \(AH\perp BC\left(H\in BC\right)\)
Ta có: \(AB^2+AC^2=BC^2\left(3^2+4^2=5^2\right)\Rightarrow\Delta ABC\) vuông tại A
\(AH.BC=AB.AC\left(=2S_{ABC}\right)\Rightarrow AH.5=3.4\Rightarrow AH=2,4\left(cm\right)\)
AD là tia p/g của \(\widehat{BAC}\left(D\in BC\right)\Rightarrow\)\(\frac{DB}{DC}=\frac{AB}{AC}=\frac{3}{4}\)
\(\Rightarrow\frac{DB}{DB+DC}=\frac{3}{3+4}\Rightarrow\frac{DB}{BC}=\frac{3}{7}\Rightarrow\frac{DB}{5}=\frac{3}{7}\Rightarrow DB=\frac{15}{7}\left(cm\right)\)
\(BM=\frac{1}{2}BC=\frac{1}{2}.5=\frac{5}{2}\left(cm\right)\)
Do đó: \(DM=BM-BD=\frac{5}{2}-\frac{15}{7}=\frac{5}{14}\left(cm\right)\)
Vậy \(S_{ADM}=\frac{1}{2}AH.DM=\frac{1}{2}.2,4.\frac{5}{14}=\frac{3}{7}\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, trung tuyến AM:
a) Cm diện tích tam giác AMB = diện tích tam giác AMC
b) Biết AB = 16 cm, AC = 12 cm, BC = 20 cm. Gọi N là trug điểm cạnh AC. Tính diện tích tam giác MBN.
a) cho tam giác ABC với đường trung tuyến AM và đường phân giác AD. Tính diện tích tam giác ADM biết AB=m, AC =n (n>m)và diện tích của tam giác ABC là S
b)cho n=7 cm, m=3cm ,hỏi diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC
Cho tam giác ABC cân tại A có trung tuyến AM , lấy O là trung điểm AM . Tia BO cắt AC tại D , tia CO cắt AB tại E . Biết diện tích của tam giác ADE = 5 cm2. Vậy diện tích tam giác ABC là ?
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM. Biết AH=3cm; HB=4cm. Hãy tính AB,AC,AM và diện tích tam giác ABC
\(HC=\dfrac{3^2}{4}=2.25\left(cm\right)\)
BC=HB+HC=6,25(cm)
AM=BC/2=3,125(cm)
\(AB=\sqrt{4\cdot6.25}=5\left(cm\right)\)
\(AC=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)
Đúng 4
Bình luận (0)
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABH\) vuông tại \(H\) , ta có :
\(AB^2=AH^2+HB^2=3^2+4^2=25\Rightarrow AB=5\left(cm\right)\)
+ ) áp dụng hệ thức về cạnh và đường cao trong tam giác vuông \(ABC\) với \(AH\) là đường cao , ta có :
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{AH^2}-\dfrac{1}{AB^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}=\dfrac{16}{225}\)
\(\Rightarrow AC=\dfrac{15}{4}\left(cm\right)\)
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABC\) vuông tại \(A\) , ta có :
\(BC^2=AB^2+AC^2=5^2+\left(\dfrac{15}{4}\right)^2=\dfrac{625}{16}\)
\(\Rightarrow BC=\dfrac{25}{4}\left(cm\right)\)
+ ) tam giác \(ABC\) vuông tại \(A\) có trung tuyến \(AM\) nên ta có :
\(AM=\dfrac{1}{2}BC=\dfrac{25}{8}\left(cm\right)\)
Đúng 2
Bình luận (1)
Câu 1. Tính: Cho tam giác ABC vuông tại A có AB = 9 cm BC = 15 cm . Đường cao AH, trung tuyến AM. Tỉnh AC, AH, BH, AM và diện tích tam giác AHM
Vì AM là trung tuyến ứng với cạnh huyền BC nên \(AM=\dfrac{1}{2}BC=7,5\left(cm\right)\)
Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=12\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=7,2\left(cm\right)\\BH=\dfrac{AB^2}{BC}=5,4\left(cm\right)\end{matrix}\right.\)
Áp dụng PTG: \(HM=\sqrt{AM^2-AH^2}=2,1\left(cm\right)\)
Vậy \(S_{AHM}=\dfrac{1}{2}HM\cdot AH=\dfrac{1}{2}\cdot2,1\cdot7,2=7,56\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời