Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy điểm E sao cho HE = HA. Chứng minh rằng:
a. AB = BE
b. Tam giác BEC vuông
Cho tam giác ABC có AB = 3cm , AC = 4cm , BC = 5cm. Kẻ AH vuông góc với BC tại H. Trên tia đối tia HA lấy điểm E sao cho HE = HA . Chứng minh rằng :
a/ Tam giác ABC vuông tại A? b/ BA = BE
c/ CH là tia phân giác góc ACE ; d/ Tam giác BEC vuông.
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔBAE có
BH là đường cao
BH là đường trung tuyến
DO đó:ΔBAE cân tại B
hay BA=BE
c: Xét ΔCAE có
CH là đường cao
CH là đường trung tuyến
Do đó:ΔCAE cân tại C
mà CB là đường cao
nên CB là tia phân giác của góc ACE
d: Xét ΔCAB và ΔCEB có
CA=CB
BA=BE
BC chung
DO đó:ΔCAB=ΔCEB
Suy ra: \(\widehat{CAB}=\widehat{CEB}=90^0\)
hay ΔBEC vuông tại E
Cho tam giác ABC, kẻ AH vuông góc với BC tại H. Gọi M là trung điểm của BC, trên tia đối của MA lấy điểm F sao cho MA = MF, trên tia đối của HA lấy điểm E sao cho HE = HA. Chứng minh rằng:
a) BE = CF
b) Tam giác AEF là tam giác vuông
Câu hỏi của Wanna One BTS is my everything - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại câu tương tự bên trên.
Cho tam giác ABC có AB = 3cm , AC = 4cm , BC = 5cm.Trên tia đối tia HA lấy điểm E sao cho HE = HA . Chứng minh rằng :
a/ Tam giác ABC vuông tại A? b/ BA = BE
c/ CH là tia phân giác góc ACE ; d/ Tam giác BEC vuông
a, Ta có :
\(AB^2+AC^2=3^2+4^2=25\)
\(BC^2=5^2=25\)
\(=> AB^2+AC^2=BC^2\)
\(=> \) △ABC vuông tại A
b, Xét △BAH và △BEH có :
\(\widehat{BHA}=\widehat{BHE}=90^o\)
BH : chung
HE = HA (GT)
=> △BAH = △BEH (c.g.c)
=> BA = BE (2 cạnh tương ứng)
c, Xét △CAH và △CEH có :
\(\widehat{CHA}=\widehat{CHE}=90^o\)
\(CH\) :chung
AH = HE (GT)
=> △CAH = △CEH (c.g.c)
=> \(\widehat{C_1}=\widehat{C_2}\)
=> CH là phân giác \(\widehat{ACE}\)
d, Xét △BAC và △BEC có :
\(BA=BE (câu a)\)
CA = CE (△CAH = △CEH)
BC : chung
=> △BAC = △BEC(c.c.c)
=> \(\widehat{BAC}=\widehat{BEC}\)
mà \(\widehat{BAC}=90^o\)
\(=> \widehat{BEC}=90^o\)
=> △BEC vuông tại E
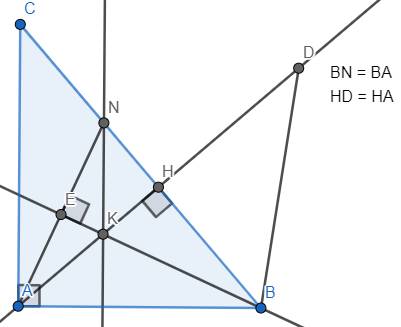
cho tam giác ABC vuông tại A (AB<AC) trên cạnh BC lấy điểm N sao cho BN=BA từ B kẻ BE vuông góc với AN (E thuộc AN) a, chứng minh tam giác ABE = tam giác NBE b, kẻ đường cao AH của tam giác ABC trên tia đối của tia HA lấy điểm D sao cho HD=HA chúng minh BA=BD c, gọi K là giao điểm của AH và BE chứng minh NK // CA
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:
- BE là cạnh chung, BN = BA (giả thuyết)
Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)
b) Theo đề ta có BH vuông góc với AD và HA = HD
Suy ra BH là đường trung trực của AD
Suy ra BA = BD (vì B nằm trên đường trung trực của AD)
c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K
Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB
Mà AC cũng vuông góc với AB, suy ra NK // CA
a. - Vì BE vuông góc với AN (gt)
=> tam giác ABE vuông tại E (tc)
tam giác NBE vuông tại E (tc)
- Xét tam giác vuông ABE và tam giác vuông NBE, có:
+ Chung BE
+ BA = BN (gt)
=> tam giác vuông ABE = tam giác vuông NBE (Cạnh huyền - cạnh góc vuông)
b. - Vì AH là đường cao của tam giác ABC (gt)
=> tam giác ABH vuông tại H
tam giác DBH vuông tại H
- Xét tam giác vuông ABH và tam giác vuông DBH, có:
+ Chung BH
+ HA = HD (gt)
=> tam giác vuông ABH = tam giác vuông DBH (2 cạnh góc vuông)
=> BA = BD (2 cạnh tương ứng)
cho tam giác ABC vuông tại A (AB<AC). Trên cạnh BC lấy điểm N sao cho BA = BN.Từ B kẻ BE vuông góc với AN (E ϵ AN)
a) chứng minh ΔABE = ΔNBE .
b) kẻ đường cao AH của tam giác ABC,trên tia đối của tia HA lấy điểm D sao cho HD =HA. Chứng minh BA= BD
c) gọi K là gaoi điểm của AH và BE .Chứng minh NK song song với CA
a: Xét ΔBEA vuông tại E và ΔBEN vuông tại Ecó
BE chung
BA=BN
=>ΔBEA=ΔBEN
b: Xet ΔBAD co
BH vừa là đường cao, vừa là trung tuyến
=>ΔBAD cân tại B
=>BA=BD
c: Xet ΔNAB có
AH,BE là đường cao
AH cắt BE tại K
=>K là trực tâm
=>NK vuông góc AB
=>NK//AC
a: Xét ΔBEA vuông tại E và ΔBEN vuông tại Ecó
BE chung
BA=BN
=>ΔBEA=ΔBEN
b: Xet ΔBAD co
BH vừa là đường cao, vừa là trung tuyến
=>ΔBAD cân tại B
=>BA=BD
c: Xet ΔNAB có
AH,BE là đường cao
AH cắt BE tại K
=>K là trực tâm
=>NK vuông góc AB
=>NK//AC
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H, trên tia đối của tia HA lấy điêm D sao cho HD= HA. Trên tia đối của tia CB lấy điểm E sao cho CE=CB. a) Chứng minh: Tam giác ACD cân b) Chứng minh: Tam giác ACE=Tam giác DCE c) Đường thẳng AC cắt DE tại K. Chứng minh: AB+BC> 2DK Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H, trên tia đối của tia HA lấy điêm D sao cho HD= HA. Trên tia đối của tia CB lấy điểm E sao cho CE=CB.
a) Chứng minh: Tam giác ACD cân
b) Chứng minh: Tam giác ACE=Tam giác DCE
c) Đường thẳng AC cắt DE tại K. Chứng minh: AB+BC> 2DK
a, Xét ∆AHC và ∆DHC có:
+CH chung
+\(\widehat{CHA}=\widehat{CHD}\left(=90^o\right)\)
+HA=HC(gt)
\(\Rightarrow\)∆HCA=∆HCD(ch-cgv)
a/ Xét tg vuông AHC và tg vuông DHC có
HC chung
HA = HD (gt)
=> tg AHC = tg DHC (Hai tg vuông có 2 cạnh góc vuông bằng nhau)
b/ K là giao của AE và CD
Xét tg vuông ABC có
\(\widehat{BAH}=\widehat{ACB}\) (cùng phụ với góc \(\widehat{ABC}\) ) (1)
tg AHC = tg DHC (cmt) => \(\widehat{DCH}=\widehat{ACB}\) (2)
Xét tg vuông ABH và tg vuông AEH có
AH chung; HB = HE (gt) => tg ABH = tg AEH (hai tg vuông có 2 cạnh góc vuông bằng nhau) \(\Rightarrow\widehat{BAH}=\widehat{EAH}\) (3)
Từ (1) (2) (3) => \(\widehat{EAH}=\widehat{DCH}\) (4)
Xét tg vuông AHE có
\(\widehat{EAH}+\widehat{AEH}=90^o\) (5)
Mà \(\widehat{AEH}=\widehat{CEK}\) (góc đối đỉnh) (6)
Từ (4) (5) (6) \(\Rightarrow\widehat{DCH}+\widehat{CEK}=90^o\Rightarrow\widehat{AKC}=90^o\)
\(\Rightarrow AK\perp CD\) mà \(CH\perp AD\) => E là trực tâm của tg ADC
c/
tg ABH = tg AEH (cmt) => AB = AE
tg AHC = tg DHC (cmt) => AC = CD
Xét tg ABC có
\(AB+AC>BC\) (trong tg tổng độ dài 2 cạnh lớn hớn độ dài cạnh còn lại)
\(\Rightarrow AE+CD>BC\)
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy D sao cho HA = HD. Trên tia đối của tia BC lấy E sao cho BE = BC. Đường thẳng AB cắt DE tại M. Chứng minh rằng M là trung điểm của DE
Xét ΔABC cân tại A có AH là đường cao
nên H là trung điểm của BC
Xét ΔEAD có
EH là trung tuyến
EB=2/3HE
=>B là trọng tâm
=>Mlà trung điểm của ED
Câu hỏi: Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC (H thuộc BC) Trên tia AH lấy điểm E sao cho HA=HE. Trên tia đối của tia CB lấy điểm F sao cho BC=CF. Gọi M là trung điểm EF.
a) Chứng minh rằng tam giác ABH=tam giác ACH.
b) Cho AB=10cm, AH=8cm. Tính độ dài BC.
c) Chứng minh rằng ba điểm A, C, M thẳng hàng.
cho tam giác ABC vuông tại A có góc ACB=65 độ.Kẻ AH vuông góc BC tại H,trên tia đối của tia HA lấy điểm E sao cho HE=HA.Gọi M là trung điểm cạnh BC,trên tia đối của MA lấy điểm D sao cho MD=MA.
a,Tính số đo góc ABC và so sánh AB và AC.
b,Chứng minh tam giác ABH bằng tam giác EBH,từ đó suy ra tam giác ABE cân tại B
c, Chứng minh tam giác BEC vuông tại E
d,Chứng minh ED song song với BC
a, áp dụng tổng 3 góc trong 1 tam giác => góc AB= 25 độ
AC < AB ( 65 độ > 25 độ)
b, Xét tam giác BHC và tam giác BHE có: BH- chung ; BHA = BHE (=90 độ) ; AH = HE ( theo đề bài)
=> hai tam giác bằng nhau (c.g.c) => BA = BE => tam giác BEA cân tại B (đpcm)
c, Dễ dàng chứng minh được tam giác BEC = tam giác BAC
=> BEC = BAC = 90 độ
=> tam giác BEC vuông tại E (đpcm)
d, Ta có: MH đi qua trung điểm của AD và AE trong tam giác ADE => NM là đường trung bình của tam giác này => MN // DE (đpcm)