Cho △ABC. Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Trên cạnh
BC lấy điểm G sao cho BG = 1/3BC. Chứng minh rằng G là trọng tâm △ACD.

Những câu hỏi liên quan
cho tam giác ABC trên tia đối của tia AB lấy điểm D sao cho BA=BD
trên cạnh BC lấy điểm G sao cho BG = 1/3 BC
a) chứng minh G là trọng tâm của tam giác ACD
b)chứng tỏ AG, DG theo thứ tự cắt các cạnh CD, AC tại trung điểm mỗi đường
cho mk một tk đi bà con ơi
ủng hộ mk đi làm ơn
Đúng 0
Bình luận (0)
cho tam giác abc trên tia đối của tia ba lấy điểm d sao cho bd=ba trên cạnh bc lấy điểm g sao cho bg=1/3 bc
a)cmr: g là trọng tâm tam giác acd
cmr ag,dg theo thứ tự cắt các cạnhk cd ,ac tại trung điểm của chúng
Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D sao cho BD=BA. Trên cạnh BC lấy điểm E sao cho BE=1/3BC. Gọi K là giao điểm của AE và CD. Chứng minh rằng DK=DC
Cho tam giác ABC có 3 góc nhọn. GỌi I là trung điểm của cạnh BC. Trên tia đối của tia IA, lấy điểm D sao cho IA=ID.
a) Chứng minh: Tam giác AIC= Tam giác DIB
b) Chứng minh: AC//BD và AC=BD
c) Treen tia đối tia AB lấy điểm G sao cho BA=BG. Trên tia đối tia AC, lấy điểm E sao cho CA=CE. Chứng minh rằng BC // GE
Cho ∆ABC vuông tại A(AB<AC). Trên cạnh BC lấy điểm D sao cho BD=BA. Tia phân giác của góc B cắt AC tại E.
a) Chứng minh: ∆ABE = ∆DBE
b) Trên tia đối của tia AB lấy điển F sao cho BF = BC, BE cắt CF tại G, chứng minh BG vuông góc CF
c) Chứng minh: D, E, F thẳng hàng.
a: Xét ΔABE và ΔDBE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔABE=ΔDBE
b: Xét ΔAEF vuông tại A và ΔDEC vuông tại D có
EA=ED
AF=DC
Do đó: ΔAEF=ΔDEC
Suy ra: EF=EC
hay E nằm trên đường trung trực của CF(1)
Ta có: BF=BC
nên B nằm trên đường trung trực của CF(2)
Từ (1) và (2) suy ra BE là đường trung trực của CF
=>BE⊥CF
hay BG⊥CF
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB < AC. Trên cạnh AC lấy AD = AB. Gọi E là trung điểm của BD. A) chứng minh AE là tia phân giác của góc BAC. B) Chứng minh AE vuông góc với BD. C) Tia AE cắt cạnh BC tại F. chứng minh BF = FD. D) Trên tia đối của tia BA lấy G sao cho BG = CD. Chứng minh G, F, D thẳng hàng.
?????????????????????????????????????????????????????
Đúng 0
Bình luận (0)
Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Trên cạnh BC lấy điểm E sao cho BE = 1/3 BC. Gọi K là giao điểm của AE và CD. Chứng minh rằng DK = KC.
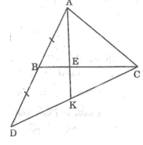
Trong ΔACD ta có:
CB là đường trung tuyến kẻ từ đỉnh C
Mặt khác:
E ∈ BC và BE = 1/3 BC (gt)
Nên: CE = 2/3 CB
Suy ra: E là trọng tâm của ΔACD.
Vì AK đi qua E nên AK là đường trung tuyến của ΔACD
Suy ra K là trung điểm của CD
Vậy KD = KC.
Đúng 0
Bình luận (0)
cho tam giác abc . trên cạnh bc lấy điểm m sao cho bm=2/3bc. trên tia đối của tia ca lấy điểm a' sao cho ca'=ca. tia am cắt ba' tại n. chứng minh rằng n là trung điểm của đoạn ba'
Cho tam giác ABC,trung tuyến AM và trọng tâm G.Trên tia đối của tia BC lấy điểm E,trên tia đối của tia BC lấy điểm E,trên tia đối của tia CB lấy điểm F sao cho BE=CF
a)chứng minh G là trọng tâm tam giác AEF
b)Gọi N là trung điểm của AF.chứng minh ba điểm E,G,N thẳng hàng
c)Gọi H là trung điểm của G,A,I là trung điểm của GE.Chứng minh IH song song với MN và IH=MN
a: BM+BE=ME
MC+CF=MF
mà BM=MC và BE=CF
nên ME=MF
Xét ΔAEF có
AM là trung tuyến
AG=2/3AM
=>G là trọng tâm
b: Xét ΔAEF có
EN là trung tuyến
G là trọng tâm
=>E,G,N thẳng hàng
c: Xét ΔGAE có GH/GA=GI/GE
nên IH//AE và IH=1/2AE
=>IH//MN và IH=MN
Đúng 0
Bình luận (0)















