CMR:không tồn tại cặp giá trị (x;y) thỏa mãn :\(x^2-2-2y^2=2011\)

Những câu hỏi liên quan
CMR:không tồn tại n \(\in\) N để n2 + 1 =3000...0
Ta thấy 3000...0 chia hết cho 3 => n^2+1 chia hết cho 3
=> n^2 chia 3 dư 2 ( vô lý vì số chính phương chia 3 dư 0 hoặc 1 )
=> ko tồn tại n thuộc N để n^2+1 = 3000...0
k mk nha
Đúng 0
Bình luận (0)
chứng minh không tồn tại cặp giá trị nguyên x,y thỏa mãn : \(x^2-2-2y^2=2011\)
CMR không tồn tại cặp giá trị nguyên (x;y) thỏa mãn:\(x^2-2-2y^2=2011\)
chứng minh rằng không tồn tại cặp giá trị nguyên (x;y) thỏa mãn :\(x^2-2-2y^2=2011\)
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
2
x
+
2
y
+
5
≥
1
, giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho...
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ 1 , giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x 2 + y 2 + 4 x + 6 y + 13 - m = 0 thuộc tập nào sau đây?
A. [8;10]
B. [5;7]
C. [1;4]
D. [-3;0]
Đáp án A
Ta có, giả thiết log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính R 1 = 2
Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m là đường tròn tâm I(-2;-3); R 2 = m
Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9
Đúng 0
Bình luận (0)
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
(
2
x
+
2
y
+
5
)
≥
1
giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m 0 thuộc tập nào sau đây?
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 ( 2 x + 2 y + 5 ) ≥ 1 giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m = 0 thuộc tập nào sau đây?
![]()
![]()
![]()
![]()
Đáp án A
Ta có, giả thiết
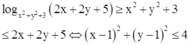
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và

Đúng 0
Bình luận (0)
Cho 12 Số tự nhiên bất kì lấy các giá trị thuộc {1;2;3} ghép 2 số cào 1 cặp ta đc 6 cặp, CMR tồn tại 2 cặp có tổng các chữ số trong cặp = nhau
Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số (x;y) thỏa mãn
e
2
x
+
y
+
1
-
e
3
x
+
2
y
x
+
y
+
1
đồng thời thỏa mãn
log
2...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số (x;y) thỏa mãn e 2 x + y + 1 - e 3 x + 2 y = x + y + 1 đồng thời thỏa mãn log 2 2 2 x + y - 1 - m + 4 log 2 x + m 2 + 4 = 0 .
A. 3
B. 4
C. 5
D. 6
Đáp án A
Ta có e 2 x + y + 1 - e 3 x + 2 y = x + y + 1 ⇔ e 2 x + y + 1 + 2 x + y + 1 = e 3 x + 2 y + 3 x + 2 y *
Xét f t = e t + t là hàm số đồng biến trên ℝ mà f 2 x + y + 1 = f 3 x + 2 y ⇒ y = 1 - x
Khi đó log 2 2 2 x + y - 1 - m + 4 log 2 x + m 2 + 4 = 0
Phương trình (1) có nghiệm khi và chỉ khi ∆ = m + 4 - 4 m 2 + 4 ≥ 0 ⇔ 0 ≤ m ≤ 8 3 .
Đúng 0
Bình luận (0)
Cho 12 số tự nhiên bất kì lấy các giá trị thuộc tập hợp(1;2;3). Ghép hai số thành một cặp ta được 6 cặp . Cmr tồn tại 2 cặp mà tổng các số trong hai cặp bằng nhau








