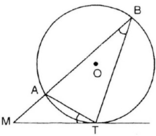
Cho điểm M nằm cố định bên ngoài (O) , vẽ tiếp tuyến MT ( T là tiếp điểm ) , vẽ cát tuyết MAB, điểm C là giao điểm của bán kính TO và dây AB . Chứng minh MC : MT2 = MA . MB

Những câu hỏi liên quan
từ 1 điểm M cố định ở bên ngoài đường tròn (O), kẻ 1 tiếp tuyến MT(T là tiếp điểm) và 1 cát tuyến MAB của đường tròn đó
a)C/m: MT2=MA.MB
b) trường hợp cát tuyến MAB đi qua tâm O. cho MT=20cm và cát tuyến dài nhất cùng xuất phát từM=50cm. tính bán kính R của đường tròn tâm O
a: Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\left(=\dfrac{1}{2}sđ\stackrel\frown{AT}\right)\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\)
b: \(MT^2=MA\cdot MB\)
=>\(MA\cdot MB=20^2=400\)
=>\(MA=\dfrac{MT^2}{MB}=\dfrac{400}{50}=8\left(cm\right)\)
MA+AB=MB
=>AB+8=50
=>AB=42(cm)
=>R=42/2=21(cm)
Đúng 1
Bình luận (0)
4. Từ M cố định bên ngoài đường tròn (o) kẻ môt tiếp tuyến MT ( T là tiếp điểm ) và một cát tuyến MAB của đường tròn đó
a) Chứng minh MT2 = MA.MB
b) trường hợp cát tuyến MAB đi qua tâm (o) . Cho MT = 20 (cm) và cát tuyến dài nhất cũng xuất phát từ M = 50 (cm) . Tính R của (O)
Giúp em bài này với mai em cần gấp !
a: Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
DO đó: ΔMTA∼ΔMBT
Suy ra: MT/MB=MA/MT
hay \(MT^2=MA\cdot MB\)
b: MB=50cm
=>MA=8cm
=>AB=42cm
=>R=21cm
Đúng 1
Bình luận (0)
Từ một điểm M cố định ở bên ngoài đường tròn (O) kẻ một tiếp tuyến MT ( T là tiếp điểm) và một cát tuyếnMAB của đường tròn đó
a) chứng minh: MT2= MA. MB
b) Kẻ TH vuông góc OM. Chứng minh: MA. MD= MO. MH
Xem chi tiết
a) Xét \(\Delta BMT\) và \(\Delta TMA\) có:
\(\widehat{M}\) chung
\(\widehat{B}=\widehat{MTA}\) (cùng chắn \(\stackrel\frown{AT}\))
\(\Rightarrow\Delta BMT\sim\Delta TMA\)
\(\Rightarrow\dfrac{MT}{MA}=\dfrac{MB}{MT}\Rightarrow MT^2=MA.MB\left(\text{Đ}PCM\right)\)
Đúng 0
Bình luận (0)
25. Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó. a) Chứng minh ta luôn có MT2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB b) Ở hình 2 cho MT = 20, MB=50cm, tính bán kính đường tròn
mình không biết đâu chỉ có thánh mới giải được
Đúng 0
Bình luận (0)
Xét \(\Delta\)MTA và \(\Delta\)MBT
có: góc M chung
\(\widehat{MTA}=\widehat{MBT}\left(=\frac{1}{2}\widebat{AT}\right)\)
=> \(\Delta\)MTA đồng dạng \(\Delta\)MBT
=> \(\frac{MT}{MB}=\frac{MA}{MT}\Rightarrow MT^2=MA.MB\left(ĐPCM\right)\)
do MT là tiếp tuyến mà M cố định nên => MT không đổi, do vậy MA.MB không đổi
Đúng 0
Bình luận (0)
25. Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
a) Chứng minh ta luôn có MT2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB
b) Ở hình 2 cho MT = 20, MB=50cm, tính bán kính đường tròn
Cho đường tròn (O: R) và một điểm M nằm ngoài đường tròn. Qua M vẽ tiếp tuyến MT và hai cát tuyến MAB, MCD của (O). Chứng minh MT^2= MA. MB= MC. MD= OM^2 - R^2
Xét đường tròn (O;R) có \(\widehat{MTA}\)là góc tạo bởi tiếp tuyến MT (tiếp điểm là T) và dây cung TA \(\Rightarrow\widehat{MTA}=\frac{1}{2}sđ\widebat{TA}\)
Mà \(\widehat{MBT}\)là góc nội tiếp chắn cung TA \(\Rightarrow\widehat{MBT}=\frac{1}{2}sđ\widebat{TA}\)
\(\Rightarrow\widehat{MTA}=\widehat{MBT}\left(=\frac{1}{2}sđ\widebat{TA}\right)\)
Xét \(\Delta MTA\)và \(\Delta MBT\), ta có: \(\widehat{BMT}\)chung; \(\widehat{MTA}=\widehat{MBT}\left(cmt\right)\)
\(\Rightarrow\Delta MTA~\Delta MBT\left(g.g\right)\)\(\Rightarrow\frac{MT}{MB}=\frac{MA}{MT}\Rightarrow MT^2=MA.MB\)(1)
Hoàn toàn tương tự, ta có \(MT^2=MC.MD\)(2)
Vì MT là tiếp tuyến tại T của (O) \(\Rightarrow MT\perp OT\)tại T \(\Rightarrow\Delta OMT\)vuông tại T
\(\Rightarrow OM^2=MT^2+OT^2\)\(\Rightarrow MT^2=OM^2-OT^2\)
Đồng thời MT là tiếp tuyến tại T của (O;R) \(\Rightarrow OT=R\)
Như vậy ta có \(MT^2=OM^2-R^2\)(3)
Từ (1), (2) và (3) ta có đpcm.
cho đường tròn ( O) và điểm M nằm bên ngoài đường tròn đó. QUA điểm M kẻ tiếp tuyến MT và cát tuyến MAB a/ CM MT mũ 2 = MA. MB b/TÍNH BÁN KÍNH ĐƯỜNG TRÒN
Từ điểm M ở ngoài ( O;R ) vẽ tiếp tuyến MC và cát tuyến MAB sao cho điểm O không nằm ngoài goc BMC. MO cắt (O) tại E,F (ME<MF)Giả sử (O;R) không đổi, điểm M cố định, cát tuyến MAB quay quanh M. Hãy tìm GTLN của tống MA+MB
Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua điểm M kẻ tiếp tuyến MT và cát tuyến MAB.
Chứng minh M T 2 = M A . M B .

( góc tạo bởi tia tiếp tuyến và dây cung, góc nội tiếp cùng chắn cung AT)

Kiến thức áp dụng
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Đúng 1
Bình luận (0)





















