b: Ta có: \(3^x+2\cdot3^{x-2}=297\)

\(\Leftrightarrow3^x=297:\dfrac{11}{9}=243\)

hay x=5

a, Ta có: 8 = 2 3 ; 10 = 2.5

BCNN(8; 10) =  2 3 .5 = 40

BC(8; 10) =B(40)= { 0; 40; 80; 120;………}

b, Ta có: 6 =2.3; 24=  2 3 . 3; 40 =  2 3 .5

BCNN( 6; 24; 40) =  2 3 .3. 5= 120

BC( 6; 24; 40)= B(120) ={ 0; 120; 240; 360….}

c, Ta có: 8 = 2 3 ; 15 = 3.5; 20 =  2 2 .5

BCNN(8; 15;20) =  2 3 .3.5 = 120

BC( 8; 15; 20)= B(120) ={ 0; 120; 240; 360….}

d, Ta có: 30 = 2.3.5; 45 =  3 2 .5

BCNN(30; 45) = 2. 3 2 .5 = 90

BC (30; 45)  và nhỏ hơn 500 = { 0; 90; 180; 270; 360;480}

e, Ta có: a nhỏ nhất khác 0, biết rằng a ⋮ 15 và a ⋮ 18

=> a = BCNN (15; 18)

Có: 15 = 3.5; 18 = 2. 3 2

BCNN(15; 18) = 2. 3 2 .5 = 90

Vậy a = 90

f, Ta có: 63 =  3 2 .7; 35 = 5.7; 105 = 3.5.7

BCNN(63; 35; 105) =  3 2 .5.7 = 315

BC(63; 35; 105) và nhỏ hơn 1000 = { 0; 315; 630; 945}

a, Ta có: 8 = 2 3 ; 10 = 2.5

BCNN(8; 10) =  2 3 .5 = 40

BC(8; 10) =B(40)= { 0; 40; 80; 120;………}

b, Ta có: 6 =2.3; 24=  2 3 . 3; 40 =  2 3 .5

BCNN( 6; 24; 40) =  2 3 .3. 5= 120

BC( 6; 24; 40)= B(120) ={ 0; 120; 240; 360….}

c, Ta có: 8 = 2 3 ; 15 = 3.5; 20 =  2 2 .5

BCNN(8; 15;20) =  2 3 .3.5 = 120

BC( 8; 15; 20)= B(120) ={ 0; 120; 240; 360….}

d, Ta có: 30 = 2.3.5; 45 =  3 2 .5

BCNN(30; 45) = 2. 3 2 .5 = 90

BC (30; 45)  và nhỏ hơn 500 = { 0; 90; 180; 270; 360;480}

e, Ta có: a nhỏ nhất khác 0, biết rằng a ⋮ 15 và a ⋮ 18

=> a = BCNN (15; 18)

Có: 15 = 3.5; 18 = 2. 3 2

BCNN(15; 18) = 2. 3 2 .5 = 90

Vậy a = 90

f, Ta có: 63 =  3 2 .7; 35 = 5.7; 105 = 3.5.7

BCNN(63; 35; 105) =  3 2 .5.7 = 315

BC(63; 35; 105) và nhỏ hơn 1000 = { 0; 315; 630; 945}

Số đó chia hết cho 18  <=>  chia hết cho cả 2 và 9

=>  số đó tận cùng là chẵn và có tổng các chữ số chia hết cho 9

Chữ số tận cùng là chẵn nên chỉ có thể lớn nhất bằng 8; mỗi chữ số còn lại bằng 9

=>  Tổng các chữ số lớn nhất là: 9+9+8 = 26

Tổng các chữ số chia hết cho 9 =>  chỉ có thể = 9 hoặc = 18

Gọi 3 chữ số là a;b;c: \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)

Gọi x là số cần tìm và y , z , f là các chữ số của nó

Nếu x chia hết cho 18 \(\Rightarrow\)x chia hết cho 2 \(\Rightarrow\)x chẵn

Theo đề bài , ta có , y , z , f tỉ lệ với 1 : 2 : 3 \(\Rightarrow\)Ta sẽ được các số : 123 ; 246 ; 369

Mà ta cũng có : x chia hết cho 3 ( do x chia hết cho 18 ) \(\Rightarrow\)Ta sẽ được các số : 396 ; 936

Vì x là bội của 18 \(\Rightarrow\)x sẽ là 936

Vậy số cần tìm là số 936

a: Gọi số cần tìm có dạng là \(\overline{abc}\)

Vì \(\overline{abc}⋮18\) nên a+b+c=18

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{1}=\dfrac{b}{2}=\dfrac{c}{3}=\dfrac{a+b+c}{1+2+3}=\dfrac{18}{6}=3\)

Do đó: a=3; b=6; c=9

Vậy: Số cần tìm là 936; 396

b: \(\Leftrightarrow\left(a^2-2\right)\left(a^2-5\right)< 0\)

\(\Rightarrow2< a^2< 5\)

\(\Leftrightarrow a^2=4\)

hay \(a\in\left\{2;-2\right\}\)

Đầu tiên, chúng ta xét xem (16a+17b)(17a+16b) chia hết cho 11 hay không. Ta biểu diễn số m = (16a+17b)(17a+16b) dưới dạng m = 272a^2 + 528ab + 272b^2.

Vì 11 là một số nguyên tố, nên theo tính chất của phép nhân, để m là một bội số của 11, thì mỗi thành phần của m cũng phải là một bội số của 11.

Ta thấy rằng 272a^2 và 272b^2 đều chia hết cho 11, vì 272 chia hết cho 11. Vì vậy, ta chỉ cần chứng minh rằng 528ab chia hết cho 11 để kết luận m là một bội số của 11.

Để chứng minh điều này, ta sử dụng tính chất căn bậc hai modulo 11. Ta biết rằng căn bậc hai của 11 là 5 hoặc -5 (vì 5^2 = 25 ≡ 3 (mod 11)). Vì vậy, ta có:

(16a+17b)(17a+16b) ≡ (5a+6b)(6a+5b) (mod 11).

Mở ngoặc, ta được:

(5a+6b)(6a+5b) ≡ 30ab + 30ab ≡ 60ab ≡ 6ab (mod 11).

Vì 6 không chia hết cho 11, nên 6ab cũng không chia hết cho 11. Do đó, ta kết luận rằng 528ab không chia hết cho 11 và m là một bội số của 11.

Tiếp theo, chúng ta cần chứng minh rằng m là một bội số của 121. Để làm điều này, ta cần chứng minh rằng m chia hết cho 121.

Một cách để chứng minh rằng m chia hết cho 121 là tìm một số tự nhiên k sao cho m = 121k. Để làm điều này, chúng ta cần tìm một số tự nhiên k sao cho (16a+17b)(17a+16b) = 121k.

Ta biểu diễn số m = (16a+17b)(17a+16b) dưới dạng m = 272a^2 + 528ab + 272b^2.

Chúng ta đã chứng minh rằng m là một bội số của 11, vậy m = 11m' với m' là một số tự nhiên.

Thay thế m vào công thức m = 272a^2 + 528ab + 272b^2, ta có:

11m' = 272a^2 + 528ab + 272b^2.

Chia cả hai vế của phương trình cho 11, ta có:

m' = 24a^2 + 48ab + 24b^2.

Như vậy, m' là một số tự nhiên. Điều này cho thấy rằng m chia hết cho 121 và m là một bội số của 121.

Để tính tổng này, chúng ta có thể sử dụng công thức tổng của một dãy số từ một số đến một số khác. Công thức này là:

Tổng = (Số lượng số trong dãy) * (Tổng của số đầu tiên và số cuối cùng) / 2,

trong đó, Số lượng số trong dãy = (Số cuối cùng - Số đầu tiên) + 1.

Áp dụng công thức này vào bài toán, ta có:

Số đầu tiên = 10, Số cuối cùng = 99, Số lượng số trong dãy = (99 - 10) + 1 = 90.

Tổng = 90 * (10 + 99) / 2 = 90 * 109 / 2 = 90 * 54,5 = 4.905.

Vậy tổng tất cả các số tự nhiên có hai chữ số không chia hết cho 3 và 5 là 4.905.

Bài toán 1: Để chứng minh số m cũng là một bội số của 121, ta sẽ sử dụng một số tính chất của phép chia.

Ta có: m = (16a + 17b)(17a + 16b) = (17a + 16b)^2 - (ab)^2

Vì m là một bội số của 11, nên ta có thể viết m dưới dạng m = 11k, với k là một số tự nhiên.

Từ đó, ta có (17a + 16b)^2 - (ab)^2 = 11k.

Áp dụng công thức (a + b)^2 - (ab)^2 = (a - b)^2, ta có (17a + 16b + ab)(17a + 16b - ab) = 11k.

Ta có thể chia hai trường hợp để xét:

Trường hợp 1: (17a + 16b + ab) chia hết cho 11. Trường hợp 2: (17a + 16b - ab) chia hết cho 11.

Trong cả hai trường hợp trên, ta đều có một số tự nhiên tương ứng với mỗi trường hợp.

Do đó, nếu m là một bội số của 11, thì m cũng là một bội số của 121.

Bài toán 2: Để tìm tổng tất cả các số tự nhiên có hai chữ số không chia hết cho 3 và 5, ta cần xác định tập hợp các số thỏa mãn điều kiện trên và tính tổng của chúng.

Các số tự nhiên hai chữ số không chia hết cho 3 và 5 có dạng AB, trong đó A và B lần lượt là các chữ số từ 1 đến 9.

Ta thấy rằng có 3 chữ số (3, 6, 9) chia hết cho 3 và 2 chữ số (5, 0) chia hết cho 5. Vì vậy, số các chữ số không chia hết cho 3 và 5 là 9 - 3 - 2 = 4.

Do đó, mỗi chữ số A có 4 cách chọn và mỗi chữ số B cũng có 4 cách chọn.

Tổng tất cả các số có hai chữ số không chia hết cho 3 và 5 là 4 x (1 + 2 + 3 + ... + 9) x 4 = 4 x 45 x 4 = 720.

Vậy tổng tất cả các số tự nhiên có hai chữ số không chia hết cho 3 và 5 là 720.

Gọi ba chữ số của số phải tìm là a, b, c

Số phải tìm là bội của 18 nên số đó chia hết cho 9 , do đó a + b + c= 9 hoặc a + b + c = 18 hoặc a + b + c =27

Theo đề bài, các chữ số của số đó tỉ lệ với 1;2;3 nên

a 1 = b 2 = c 3

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

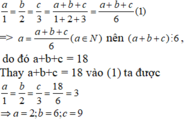
Lại có số phải tìm là bội của 18 nên chữ số hàng đơn vị của nó là số chẵn, do đó có hai số thỏa mãn đề bài là 396;936

Đáp án cần chọn là C