cho tam giác ABC, góc A=90 độ, đường phân giác AD cắt BC tại D. Cho DB=15cm, DC=20cm. Tính AB,AC
help me pleaseee
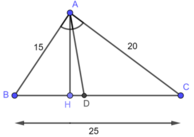
Cho tam giác ABC có AB=15cm, AC=20cm,BC=25cm. Đường phân giác góc BAC cắt BC tại D
a) tính độ dài DB và DC
b) tính tỉ số diện tích tam giác ABC và tam giác ACD
Hình tự vẽ lấy nhé
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
\(\Rightarrow\frac{DB}{DC}=\frac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\frac{DB}{DC}=\frac{15}{20}\)
\(\Rightarrow\frac{DB}{DB+DC}=\frac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
\(\Rightarrow\frac{DB}{BC}=\frac{15}{35}\Rightarrow DB=\frac{15}{35}.BC=\frac{15}{35}.25=\frac{75}{7}\left(cm\right)\)
b) Kẻ \(AH\perp BC\)
Ta có: \(S_{ABD}=\frac{1}{2}AH.BD\)
\(S_{ACD}=\frac{1}{2}AH.CD\)
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.CD}=\frac{BD}{DC}\)
Mà \(\frac{DB}{DC}=\frac{15}{12}=\frac{3}{4}\)
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{3}{4}\left(đpcm\right)\)
Tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân giác góc BAC cắt cạnh BC tại D. Tính độ dài các đoạn thẳng DB và DC.
Trong △ ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: ![]() (tính chất đường phân giác)
(tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên ![]()
Suy ra: ![]() (tính chất tỉ lệ thức)
(tính chất tỉ lệ thức)
Suy ra: 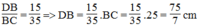
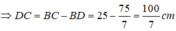
1) Cho tam giác ABC vuông tại A,đường phân giác AD.Tính độ dài AB,A C biết DB=15cm,DC=20cm
2) Cho tam giác ABC vuông tại A ,AB=15cm,AC=20cm,đường cao AH,tia phân giác của góc HAB cắt cạnh HB tại D ,tia phân giác của góc HAC cắt HC tại E.
a) Tính độ dài AH
b) Tính độ dài HD,HE
Bài 1:
Xét ΔABC có AD là phân giác
nen AB/BD=AC/CD
=>AB/3=AC/4
Đặt AB/3=AC/4=k
=>AB=3k; AC=4k
Ta có: \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow25k^2=35^2\)
=>k2=49
=>k=7
=>AB=21cm; AC=28cm
Cho tam giác ABC. Tia phân giác góc A cắt BC tại D. Qua C kẻ đường thẳng song song với AB cắt AD tại E.
a) Chứng minh: ∆ABD ∽ ∆ECD
b) Cho AB = 8cm, AC = 12cm, BC =15cm. Tính DB, DC.
Cho tam giác ABC. Tia phân giác góc A cắt BC tại D. Qua C kẻ đường thẳng song song với AB cắt AD tại E.
a) Chứng minh: ∆ABD ∽ ∆ECD
b) Cho AB = 8cm, AC = 12cm, BC =15cm. Tính DB, DC.
a: Xét ΔABD và ΔECD có
\(\widehat{ADB}=\widehat{EDC}\)
\(\widehat{ABD}=\widehat{ECD}\)
Do đó; ΔABD\(\sim\)ΔECD
b: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/8=DC/12
=>DB/2=DC/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{2}=\dfrac{DC}{3}=\dfrac{DB+DC}{2+3}=\dfrac{15}{5}=3\)
Do đó: DB=6cm; DC=9cm
Cho tam giác ABC. Tia phân giác góc A cắt BC tại D. Qua C kẻ đường thẳng song song với AB cắt AD tại E.
a) Chứng minh: ∆ABD ∽ ∆ECD
b) Cho AB = 8cm, AC = 12cm, BC =15cm. Tính DB, DC.
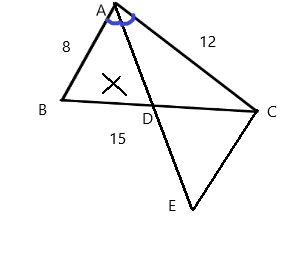
a) Vì AB//CE (gt)
=> BAD = CED (so le trong)
Xét tam giác ABD và tam giác ECD có
BAD = CED (cmt)
ADB = EDC (đối đỉnh)
=> Tam giác ABD đồng dạng với tam giác ECD
b) Đặt BD là x, ta có:
CD = BC - BD = 15 - x
Xét tam giác ABC có AD là đường phân giác (gt) nên
=> BD/DC = AB/AC (Tính chất đường phân giác trong tam giác)
Thay số: x/15 - x = 8/12
=> 12x = 8(15 - x)
(=) 12x = 120 - 8x
(=) 20x = 120
(=) x = 6
=> BD = 6
=> CD = BC - BD = 15 - 6 = 9 cm
Cho tam giác ABC. Tia phân giác góc A cắt BC tại D. Qua C kẻ đường thẳng song song với AB cắt AD tại E.
a) Chứng minh: ∆ABD ∽ ∆ECD
b) Cho AB = 8cm, AC = 12cm, BC =15cm. Tính DB, DC.
Cho tam giác ABC. Tia phân giác góc A cắt BC tại D. Qua C kẻ đường thẳng song song với AB cắt AD tại E.
a) Chứng minh: ∆ABD ∽ ∆ECD
b) Cho AB = 8cm, AC = 12cm, BC =15cm. Tính DB, DC.
a: Xét ΔABD và ΔECD có
\(\widehat{ADB}=\widehat{EDC}\)
\(\widehat{ABD}=\widehat{ECD}\)
Do đó; ΔABD\(\sim\)ΔECD
b: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/8=DC/12
=>DB/2=DC/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{2}=\dfrac{DC}{3}=\dfrac{DB+DC}{2+3}=\dfrac{15}{5}=3\)
Do đó: DB=6cm; DC=9cm
Cho tam giác ABC. Tia phân giác góc A cắt BC tại D. Qua C kẻ đường thẳng song song với AB cắt AD tại E.
a) Chứng minh: ∆ABD ∽ ∆ECD
b) Cho AB = 8cm, AC = 12cm, BC =15cm. Tính DB, DC.
a: Xét ΔABD và ΔECD có
\(\widehat{ADB}=\widehat{EDC}\)
\(\widehat{ABD}=\widehat{ECD}\)
Do đó; ΔABD\(\sim\)ΔECD
b: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/8=DC/12
=>DB/2=DC/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{2}=\dfrac{DC}{3}=\dfrac{DB+DC}{2+3}=\dfrac{15}{5}=3\)
Do đó: DB=6cm; DC=9cm