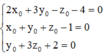Gọi (x0; y0) là nghiệm của phương trình: x2+9y2-4x+7=2y(3x-7) sao cho y0 đạt giá trị lớn nhất. Tổng x0+y0 có giá trị bằng:
A. -4 B. \(\frac{-5}{2}\) C. \(\frac{-3}{2}\) D. -5
Những câu hỏi liên quan
Gọi x0 là nghiệm nguyên của phương trình
5
x
.
8
x
x
+
1
100
. Tính giá trị của biểu thức P x0(5 - x0)( x0 + 8). A.40 B.50 C.60 D.70
Đọc tiếp
Gọi x0 là nghiệm nguyên của phương trình 5 x . 8 x x + 1 = 100 . Tính giá trị của biểu thức P = x0(5 - x0)( x0 + 8).
A.40
B.50
C.60
D.70
Chọn C.
Điều kiện. x ≠ -1
Phương trình tương đương 
Lấy ln hai vế của , ta được 
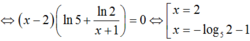
Suy ra x0 = 2 và P = 60.
Đúng 0
Bình luận (0)
= x0(5 - x0)( x0 + 8).
Cho hàm số
y
f
x
có đạo hàm trên tập K. Gọi
x
0
∈
K
, khi đó
x
x
0
được gọi là điểm cực đại của hàm số
y
f
x
nếu A.
f
x
đổi dấu khi x đi qua giá trị
x
x...
Đọc tiếp
Cho hàm số y = f x có đạo hàm trên tập K. Gọi x 0 ∈ K , khi đó x = x 0 được gọi là điểm cực đại của hàm số y = f x nếu
A. f ' x đổi dấu khi x đi qua giá trị x = x 0 .
B. f ' x = 0
C. f ' x đổi dấu từ âm sang dương khi x đi qua giá trị x = x 0 .
D. f ' x đổi dấu từ dương sang âm khi x đi qua giá trị x = x 0 .
Gọi
x
0
là một nghiệm của phương trình 5x – 12 4 - 3x. Hỏi x0 còn là nghiệm của phương trình nào dưới đây? A. 2x – 4 0 B. -x – 2 0 C.
x
2
+ 4 0 D. 9 –
x
2
-5
Đọc tiếp
Gọi x 0 là một nghiệm của phương trình 5x – 12 = 4 - 3x. Hỏi x0 còn là nghiệm của phương trình nào dưới đây?
A. 2x – 4 = 0
B. -x – 2 = 0
C. x 2 + 4 = 0
D. 9 – x 2 = -5
Gọi
∆
là tiếp tuyến tại điểm M(
x
0
;
y
0
),
x
0
0 thuộc đồ thị hàm số y
x
+
2
x
+
1
sao cho khoảng cách từ I(-1;1) đến
∆
đạt giá trị lớn nhất, khi đó x0, y0 bằng A. -2. B. 2. C. -1. D. 0.
Đọc tiếp
Gọi ∆ là tiếp tuyến tại điểm M( x 0 ; y 0 ), x 0 < 0 thuộc đồ thị hàm số y = x + 2 x + 1 sao cho khoảng cách từ I(-1;1) đến ∆ đạt giá trị lớn nhất, khi đó x0, y0 bằng
A. -2.
B. 2.
C. -1.
D. 0.
Chọn D.
Gọi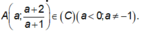 
Phương trình tiếp tuyến của (C) tại A là:
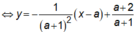
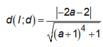
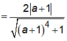
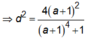
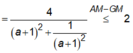
Dấu “=” xảy ra khi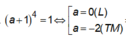 
=> M(-2;0)
Suy ra 
Đúng 0
Bình luận (0)
Gọi
x
0
log
a
b
là nghiệm của phương trình
log
3
3
x
+
1
.
log
3
3
x
+
2
+...
Đọc tiếp
Gọi x 0 = log a b là nghiệm của phương trình log 3 3 x + 1 . log 3 3 x + 2 + 9 = 3 . Biết x 0 ∈ 0 ; 1 . Khi đó, khẳng định nào sau đây là đúng?
A. a + b = 6
B. a + b = 4
C. a + b = 5
D. a + b = 9
Gọi
x
0
log
a
b
là nghiệm của phương trình
log
3
3
x
+
1
.
log
3
3
x
+
2
+...
Đọc tiếp
Gọi x 0 = log a b là nghiệm của phương trình log 3 3 x + 1 . log 3 3 x + 2 + 9 = 3 . Biết x 0 ∈ 0 ; 1 . Khi đó, khẳng định nào sau đây là đúng?
A. a + b = 6
B. a + b = 4
C. a + b = 5
D. a + b = 9
Gọi
x
0
là hoành độ giao điểm của đồ thị hàm số
y
x
2
+
x
+
3
x
−
2
và đường thẳng
y
x
Khi đó
x
0
bằng A.
x...
Đọc tiếp
Gọi x 0 là hoành độ giao điểm của đồ thị hàm số y = x 2 + x + 3 x − 2 và đường thẳng y = x Khi đó x 0 bằng
A. x 0 = − 1.
B. x 0 = 0.
C. x 0 = 1.
D. x 0 = − 2.
Đáp án A
Phương trình hoành độ giao điểm:
x 2 + x + 3 x − 2 = x x ≠ 2 ⇒ x 2 + x + 3 = x 2 − 2 x ⇔ x = − 1 t / m .
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(1;1;1);N(1;0;-2),P(0;1;-1). Gọi
G
(
x
0
;
y
0
;
z
0
)
là trực tâm tam giác MNP. Tính
x
0
+
z
0
A. 0 B.
-
13
7
C.
5...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(1;1;1);N(1;0;-2),P(0;1;-1). Gọi G ( x 0 ; y 0 ; z 0 ) là trực tâm tam giác MNP. Tính x 0 + z 0
A. 0
B. - 13 7
C. 5 2
D. -5
M(1;1;1);N(1;0;-2),P(0;1;-1) ⇒ N P ⇀ = - 1 ; 1 ; 1 ; M P ⇀ = - 1 ; 0 ; - 2
⇒ N P ⇀ ; M P ⇀ = - 2 ; - 3 ; 1
Phương trình mặt phẳng (MNP) là
G là trực tâm tam giác MNP
⇔
⇔
⇔
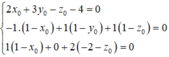
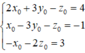
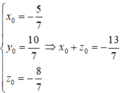
Chọn đáp án B.
Đúng 0
Bình luận (0)
Gọi
x
0
là giá trị thỏa mãn
5
7
:
x
-
2
5
1
3
A.
x
0
1
B.
x
0...
Đọc tiếp
Gọi x 0 là giá trị thỏa mãn 5 7 : x - 2 5 = 1 3
A. x 0 < 1
B. x 0 = 1
C. x 0 > 1
D. x 0 = - 1
Trong không gian với hệ trục tọa độ Oxyz, cho 3 điểm M(1;1;1), N(1;0;
-
2), P(0;1;
-
1). Gọi G(x0;y0;z0) là trực tâm tam giác MNP. Tính x0 + z0 A.
-
5 B. 5/2 C.
-
13/7 D. 0
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho 3 điểm M(1;1;1), N(1;0; - 2), P(0;1; - 1). Gọi G(x0;y0;z0) là trực tâm tam giác MNP. Tính x0 + z0
A. - 5
B. 5/2
C. - 13/7
D. 0
Đáp án C
Phương pháp: G là trực tâm tam giác MNP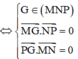 
Cách giải: G(x0;y0;z0) là trực tâm tam giác MNP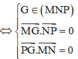 
Mặt phẳng (MNP) có một VTPT 
Phương trình (MNP): 2x+3y-z-4=0
Từ (1),(2),(3), suy ra 
Đúng 0
Bình luận (0)