Phương trình tương đương

\(\left\{{}\begin{matrix}\left(m-1\right)x+2=\left(m+1\right)\left(x-2\right)\\x\ne2\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}\left(m-1\right)x+2=\left(m+1\right)x-2m-2\\x\ne2\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}\left(m-1-m-1\right)x=-2m-4\\x\ne2\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}-2x=-2m-4\\x\ne2\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}x=m+2\\x\ne2\end{matrix}\right.\)

Nếu m = 0 thì phương trình vô nghiệm

Nếu m ≠ 0 thì S = {m + 2}

\(PT\Leftrightarrow m^2x-m^2-5mx+m+6x+2=0\\ \Leftrightarrow x\left(m^2-5m+6\right)=m^2-m-2\\ \Leftrightarrow x\left(m-2\right)\left(m-3\right)=\left(m-2\right)\left(m+1\right)\)

Với \(m\ne2;m\ne3\)

\(PT\Leftrightarrow x=\dfrac{\left(m-2\right)\left(m+1\right)}{\left(m-2\right)\left(m-3\right)}=\dfrac{m+1}{m-3}\)

Với \(m=2\Leftrightarrow0x=0\left(vsn\right)\)

Với \(m=3\Leftrightarrow0x=4\left(vn\right)\)

Vậy với \(m\ne2;m\ne3\) thì PT có nghiệm duy nhất \(x=\dfrac{m+1}{m-3}\), với \(m=2\) thì PT có vô số nghiệm và với \(m=3\) thì PT vô nghiệm

\(m\left(x-m\right)\le4x+5.\left(1\right)\\ \Leftrightarrow mx-m^2-4x-5\le0.\\ \Leftrightarrow\left(m-4\right)x\le5+m^2.\circledast\)

+) Nếu \(m-4>0.\Leftrightarrow m>4.\)

Khi \(\circledast\) có nghiệm: \(x\le\dfrac{5+m^2}{m-4}.\)

+) Nếu \(m-4< 0.\Leftrightarrow m< 4.\)

Khi \(\circledast\) có nghiệm: \(x\ge\dfrac{5+m^2}{m-4}.\)

+) Nếu \(m-4=0.\) \(\Leftrightarrow m=4.\)

Thay vào \(\circledast\) ta có: 

\(0x\le5+4^2.\Leftrightarrow0x\le21\) (vô lý).

Kết luận: 

Với \(m>4\) thì (1) có tập nghiệm \(S=\) \((-\infty;\dfrac{5+m^2}{m-4}].\)

Với \(m< 4\) thì (1) có tập nghiệm \(S=\) \([\dfrac{5+m^2}{m-4};+\infty).\)

Với \(m=4\) thì (1) có tập nghiệm \(S=\) \(\phi.\)

 

a. \(\frac{mx+5}{10}\)+ \(\frac{x+m}{4}\)=\(\frac{m}{20}\)

\(\frac{2mx+10}{20}\)+ \(\frac{5x+5m}{20}\)=\(\frac{m}{20}\)

2mx +10 + 5x +5m =m

x(2m+5)= -4m -10(1)

* 2m+5= 0 => m=-5/2

(1)<=> 0x=0 vậy phương trình 1 vô số nghiệm

* 2m+5 \(\ne\)0=> m\(\ne\)-5/2

pt (1)có nghiệm duy nhất là x= -2(2m+5): (2m+5)=-2

vậy với m=-5/2 phương trình đã cho vô số nghiệm

m\(\ne\)-5/2 phương trình đã cho có nghiệm duy nhất là x=-2

 

b.(m+2)x+ 4(2m+1)= \(m^2\)+4(m-1)

(m+2)x= \(m^2\)+ 4m-4-8m -4

(m+2)x=\(m^2\)-4m-8(1)

* với m+2=0 => m=-2

pt(1)<=> 0x=4

vậy phương trinh đã cho vô nghiệm

* với m+2\(\ne\)0=> m\(\ne\)-2

phương trình đã cho có nghiệm duy nhất là x=( \(m^2\)-4m-8):(m-2)

Phương trình (1) ⇔ x = -3m + 2

    Phương trình (2) ⇔ 3x = m - 2 ⇔ x = (m - 2) / 3

    Vậy với mọi giá trị của m phương trình có nghiệm là:

     x 1  = -3m + 2 và x 2  = (m - 2) / 3

a) ⇔ (m – 3)x = 2m + 1.

Nếu m ≠ 3 phương trình có nghiệm duy nhất x = . Nếu m = 3 phương trình trở thành 0x = 7. Vô nghiệm.

b) ⇔ (m² – 4)x = 3m – 6.

Nếu m² – 4 ≠ 0 ⇔ m ≠ ± 2, có nghiệm x = . Nếu m = 2, phương trình trở thành 0x = 0, mọi x ∈ R đều nghiệm đúng phương trình. Nếu m = -2, phương trình trở thành 0x = -12. Vô nghiệm.

c) ⇔ 2(m – 1)x = 2(m-1).

Nếu m ≠ 1 có nghiệm duy nhất x = 1. Nếu m = 1 mọi x ∈ R đều là nghiệm của phương trình.

Lời giải

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge m\left(1\right)\\\left(3x+2m\right)^2=\left(x-m\right)^2\left(2\right)\end{matrix}\right.\)

(2)\(\Leftrightarrow9x^2+12xm+4m^2=x^2-2mx+m^2\)

\(\Leftrightarrow8x^2+14mx+3m^2=0\)

\(\Delta'_x=49m^2-24m^2=25m^2\ge0\forall m\) => (2) luôn có nghiệm với mợi m

\(x=\dfrac{5\left|m\right|-7m}{8}\) (3)

so sánh (3) với (1)

\(\dfrac{5\left|m\right|-7m}{8}\ge m\Leftrightarrow\left|m\right|\ge3m\)(4)

m <0 hiển nhiên đúng

xét khi m\(\ge\)0

\(\left(4\right)\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m^2\ge9m^2\end{matrix}\right.\)\(\Rightarrow m\le0\)\(\Leftrightarrow m=0\)

Biện luận

(I)với m <0 có hai nghiệm

\(\left\{{}\begin{matrix}x_1=\dfrac{-3m}{2}\\x_2=\dfrac{-m}{4}\end{matrix}\right.\)

(II) với m= 0 có nghiệm kép x=0

(III) m>0 vô nghiệm

 

 

b) \(\left|2x+m\right|=\left|x-2m+2\right|\Leftrightarrow\left[{}\begin{matrix}2x+m=x-2m+2\left(1\right)\\2x+m=-\left(x-2m+2\right)\left(2\right)\end{matrix}\right.\)
Xét (1): \(2x+m=x-2m+2\Leftrightarrow x=-3m+2\).
Xét (2): \(2x+m=-\left(x-2m+2\right)\Leftrightarrow x=\dfrac{m-2}{3}\)
Biện luận:
Với mọi m phương trình đều có hai nghiệm:
\(x=-3m+2;x=\dfrac{m-2}{3}\).

c) \(mx^2+\left(2m-1\right)x+m-2=0\)
- Với m = 0 phương trình trở thành:
\(0.x^2+\left(2.0-1\right)x+0-2=0\)\(\Leftrightarrow-x-2=0\)\(\Leftrightarrow x=-2\)
- Xét \(m\ne0\)
\(\Delta=\left(2m-1\right)^2-4m.\left(m-2\right)=4m+1\)
Nếu \(4m+1>0\Leftrightarrow m>\dfrac{-1}{4}\) phương trình có hai nghiệm phân biệt:
\(x_1=\dfrac{-\left(2m-1\right)+\sqrt{4m+1}}{2m}\);
\(x_2=\dfrac{-\left(2m-1\right)-\sqrt{4m+1}}{2m}\)
Nếu \(4m+1=0\Leftrightarrow m=\dfrac{-1}{4}\) phương trình có nghiệm kép:
\(x_1=x_2=\dfrac{-\left(2m-1\right)}{2m}=\dfrac{-\left(2.\dfrac{-1}{4}-1\right)}{2.\dfrac{-1}{4}}=-3\)
Nếu \(4m+1< 0\Leftrightarrow m< \dfrac{-1}{4}\) phương trình vô nghiệm.
Biện luận:
\(m=0\) phương trình có một nghiệm là x = -2.
\(m\ge\dfrac{-1}{4}\) và \(m\ne0\) phương trình có hai nghiệm phân biệt:
\(x_1=\dfrac{-\left(2m-1\right)+\sqrt{4m+1}}{2m}\); \(x_2=\dfrac{-\left(2m-1\right)-\sqrt{4m+1}}{2m}\)
\(m\le\dfrac{-1}{4}\) phương trình có nghiệm kép:\(x_1=x_2=3\)

(2m + 1)x – 2m = 3x – 2

⇔ (2m + 1)x – 3x = 2m – 2

⇔ (2m + 1 – 3).x = 2m – 2

⇔ (2m – 2).x = 2m – 2 (3)

     + Xét 2m – 2 ≠ 0 ⇔ m ≠ 1, pt (3) có nghiệm duy nhất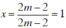 

     + Xét 2m – 2 = 0 ⇔ m = 1, pt (3) ⇔ 0.x = 0, phương trình có vô số nghiệm.

Kết luận :

+ Với m = 1, phương trình có vô số nghiệm

+ Với m ≠ 1, phương trình có nghiệm duy nhất x = 1.