C/m nếu AB+CD=AD+BC thì tứ giác ABCD ngoại tiêps đường tròn.

Những câu hỏi liên quan
Tứ giác ABCD nội tiếp đường tròn đường kính AD, có AB = BC = 4√3cm; CD = 4cm. Bán kính đường tròn ngoại tiếp tứ giác ABCD là ............ cm.
Lời giải:
Gọi giao của $BO$ và $AC$ là $H$
Vì $BA=BC; OA=OC$ nên $BO$ là trung trực của $AC$
$\Rightarrow BO$ vuông góc với $AC$ tại trung điểm $H$ của $AC$.
Do đó $HO$ là đường trung bình ứng với cạnh $CD$ của tam giác $ACD$
$\Rightarrow HO=2$
$BH=BO-HO=R-2$
Theo định lý Pitago:
$BC^2-BH^2=CH^2=CO^2-HO^2$
$\Leftrightarrow (4\sqrt{3})^2-(R-2)^2=R^2-2^2$
$\Leftrightarrow 48-(R-2)^2=R^2-4$
$\Rightarrow R=6$ (cm)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD ngoại tiếp đường tròn I. Chứng minh AB + CD = AD + BC ( định lý Pithot thuận )
Tứ giác ABCD ngoại tiếp đường tròn (O), vẽ các nửa đường tròn đường kính AD và BC ra phía ngoài của tứ giác. Biết AB + CD = 10cm. Tính tổng các độ dài của hai nửa đường tròn này.
Ta có : A là giao điểm của 2 đường tiếp tuyến tại E và G của O =>AG=AE
Chứng minh tương tự,ta được BE=BH
=>AG+BH=AB
Tương tự,ta có DG+HC=CD
=>AB+CD=AD+BC=10cm
nửa đường tròn tâm G: 2AG.π/2=AG.π=1/2.AD.π
nửa đường tròn tâm H:1/2.BC.π
=> S=1/2(AD+BC)π=5π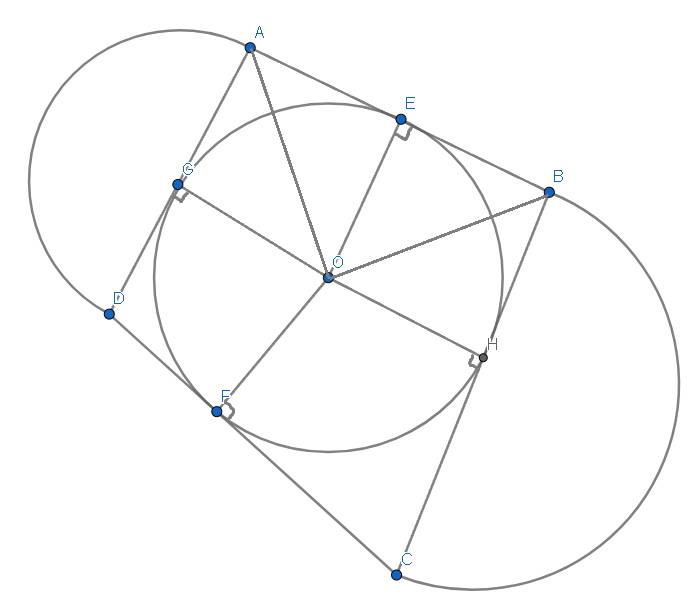
Đúng 0
Bình luận (0)
Tứ giác abcd nội tiếp đường tròn đường kính AB, có AB=BC=4 căn 3 cm, CD=4cm. Bán kính đường tròn ngoại tiếp tứ giác ABCD là?
Gọi M là điểm bất kì thuộc đường tròn (O) ngoại tiếp tứ giác ABCD. Khoảng cách từ M đến đường thẳng AB, BC, CD, AD theo thứ tự là MH, MK, MI, MN. Chứng minh rằng MH.MI = MK.MN.
Cho tứ giác ABCD nội tiếp đường tròn (O) . C/m:
AB . CD + AD . BC = AC.BD
Lấy điểm I trên đoạn thẳng AC . Ta có hình vẽ sau:
Khi đó: \(AB.CD=IA.BD\Leftrightarrow\frac{AB}{AI}=\frac{DB}{DC}\)
Mà \(\widehat{BAI}=\widehat{BDC}\)nên \(\Delta BAI\infty\Delta BDC\)(c.g.c)
Từ đó \(\widehat{IBC}=\widehat{BDC}\)
Với cách chọn điểm I như trên ta được:
\(\widehat{IBC}=\widehat{ABD}\Rightarrow\Delta IBC\infty\Delta ABD\) (g.g)
Từ đó suy ra AB . BC = IC . BD (đpcm)
Đúng 0
Bình luận (0)
Cho tứ giác lồi ABCD. CMR nếu tồn tại một đường tròn nội tiếp tứ giác và một đường tròn tiếp xúc với các cạnh kéo dài của nó thì:
a) AB+DC=AD+BC
b) AB-DC=AD-BC
c) Các đường chéo của tứ giác vuông góc với nhau.
1.Cho tứ giác ABCD ngoại tiếp đường tròn tâm O. Gọi M,N,P,Q là các tiếp điểm của đường tròn tâm O với AB,BC,CD,DA. CMR NP,MQ,BD đồng quy
2. Cho HBH ABCD. Lấy S trong HBH. Qua S kẻ các đường thẳng song song với AB cắt AD,BC lần lượt tại M,P. kẻ đường thẳng song song với AD cắt AB,CD lần lượt tại N,Q. Chứng minh AS,PQ,DP đồng quy tại một điểm.
gọi I là giao điểm của QM và BD
Áp dụng định lí Mê-nê-la-uyt cho \(\Delta ABD\)
\(\frac{AQ}{QD}.\frac{ID}{IB}.\frac{MB}{MA}=1\)
vì Q,M,I thẳng hàng , kết hợp với MA = QA suy ra \(\frac{MB}{QD}.\frac{ID}{IB}=1\)
Ta có : MB = NB ; DP = DQ ; PC = NC
nên \(\frac{NB}{DP}.\frac{ID}{IB}=1\Rightarrow\frac{PC}{PD}.\frac{ID}{IB}.\frac{NB}{NC}=1\)
do đó , theo định lí Mê-nê-la-uyt thì I,N,P thẳng hàng
từ đó ta được đpcm
cho tứ giác ABCD nội tiếp (o) có AD cắt BC tại E , AB cắt CD tại F . Gọi EI là đường đối trung của tam giác EAB ( I nằm trên đường tròn ngoại tiếp tam giác AEB) . FI cắt (o) lần lượt tại M , N . Chứng tỏ rằng IM = IN .














