Cho phương trình x2-7x+10=0 không giải phương trình tính x12-x22
Cho phương trình 2 x 2 - x - 7 = 0, không giải phương trình
b) Tính x 1 2 + x 2 2
Cho phương trình x2 + 5x − 4 = 0 . Gọi x1 ; x2 là hai nghiệm của phương trình. Không giải phương trinh, hăy tính giá trị biểu thức
Q = x12 + x22 + 6x1 x 2.
Q=(x1+x2)^2-2x1x2+6x1x2
=(-5)^2+4*(-4)
=25-16=9
Áp dụng Viét có: `{(x_1+x_2=-b/a=-5),(x_1.x_2=c/a=-4):}`
Ta có: `Q=(x_1+x_2)^2+4x_1.x_2`
`<=>Q=(-5)^2+4.(-4)`
`<=>Q=9`
Gọi x 1 ; x 2 là nghiệm của phương trình x 2 - 5 x + 2 = 0 . Không giải phương trình, tính giá trị của biểu thức A = x 1 2 + x 2 2
A. 20
B. 21
C. 22
D. 23
Đáp án B
Phương trình x 2 - 5 x + 2 = 0 có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có:
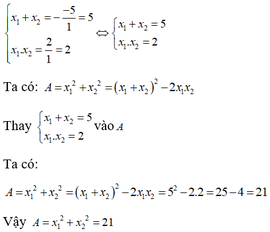
Gọi x 1 ; x 2 là nghiệm của phương trình x 2 − 5 x + 2 = 0 . Không giải phương trình, tính giá trị của biểu thức A = x 1 2 + x 2 2
A. 20
B. 21
C. 22
D. 22
Phương trình x 2 − 5x + 2 = 0 có = ( − 5 ) 2 – 4.1.2 = 17 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = 5 x 1 . x 2 = 2
Ta có
A = x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 – 2 x 1 . x 2 = 5 2 – 2 . 2 = 21
Đáp án: B
Gọi x 1 ; x 2 là nghiệm của phương trình x 2 - 5x + 2 = 0. Không giải phương trình, tính giá trị của biểu thức A = x 1 2 + x 2 2
A. 20
B. 21
C. 22
D. 23
Đáp án B
Phương trình x 2 - 5 x + 2 = 0 có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có:
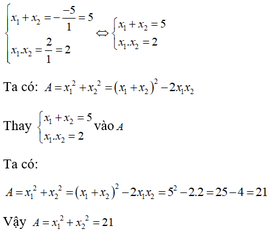
Cho phương trình 5x2 - 2x - 7 = 0. a) Không giải phương trình, tính tổng và tích hai nghiệm. b) Tính giá trị của biểu thức A = x12 + x22 – x1. x2
a. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2}{5}\\x_1x_2=-\dfrac{7}{5}\end{matrix}\right.\)
b.
\(A=x_1^2+x_2^2-x_1x_2=\left(x_1+x_2\right)^2-3x_1x_2\)
\(=\left(\dfrac{2}{5}\right)^2-3\left(-\dfrac{7}{5}\right)=\dfrac{109}{25}\)
Gọi x 1 ; x 2 là nghiệm của phương trình 2 x 2 − 11 x + 3 = 0 . Không giải phương trình, tính giá trị của biểu thức A = x 1 2 + x 2 2
A. 109 4
B. 27
C. − 109 4
D. 121 4
Phương trình 2 x 2 − 11x + 3 = 0 3 = 97 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = 11 2 x 1 . x 2 = 3 2
Ta có
A = x 1 2 + x 2 2 = x 1 + x 2 2 - 2 x 1 x 2 1 + x 2 ) = 11 2 2 − 2. 3 2 = 109 4
Đáp án: A
Bài 2: Gọi x1, x2 là hai nghiệm của phương trình: x2 + x - 2 + √2 = 0. Không giải phương trình, tính các giá trị của các biểu thức sau:
A = \(\dfrac{1}{x_1}\)+ \(\dfrac{1}{x_2}\) B = x12 + x22
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=-2+\sqrt{2}\end{matrix}\right.\)
\(A=\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1x_2}=\dfrac{-1}{-2+\sqrt{2}}=\dfrac{2+\sqrt{2}}{2}\)
\(B=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(-1\right)^2-2\left(-2+\sqrt{2}\right)=5-2\sqrt{2}\)
Cho phương trình 2x^2 - 6x +3 =0
a) chứng tỏ phương trình trên có 2 nghiệm phân biệt x1 x2
b) Không giải phương trình để tìm 2 nghiệm x1, x2, hãy tính giá trị của biểu thưc A= 2x1 +x1.x2 +2x2 phần x12 .x2 +x1.x22