Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. G là trọng tâm tam giác A'BC. Tính 3AG2.

Những câu hỏi liên quan
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a và G là trọng tâm tam giác A'BC. Tính 3AG^2.Ai giúp em với ạ❤
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh a. Tính khoảng cách từ điểm A đến mặt phẳng (ABC) theo a. A.
a
2
2
B.
a
3
3
C.
a
3...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Tính khoảng cách từ điểm A đến mặt phẳng (A'BC) theo a.
A. a 2 2
B. a 3 3
C. a 3 2
D. a 2 3
Đáp án A
Ta có: 1 d 2 = 1 A B 2 + 1 A A ' 2 = 2 a 2 ⇒ d = a 2 2 .
Đúng 0
Bình luận (0)
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB=a, góc giữa 2 mặt phẳng (A'BC) và (ABC) bằng 60 độ. Gọi G là trọng tâm của tam giác A'BC.
Tính thể tích của khối lăng trụ đã cho và bán kính mặt cầu ngoại tiếp tứ diện GABC theo a
_ Thể tích khối lăng trụ :
Gọi D là trung điểm của BC ta có : \(BC\perp AD\Rightarrow BC\perp A'D\Rightarrow\widehat{ADA'}=60^0\)
Ta cso \(AA'=AD.\tan\widehat{ADA'}=\frac{3a}{2};S_{ABC}=\frac{a^2\sqrt{3}}{4}\)
Do đó \(V_{ABC.A'B'C'=}S_{ABC}.AA'=\frac{3a^2\sqrt{3}}{8}\)
- Bán kính mặt cầu ngoại tiếp tứ diện GABC :
Ta có I là giao điểm của GH với đường trung trực của AG trong mặt phẳng (AGH)
Gọi E là trung điểm của AG, ta có :
\(R=GI=\frac{GE.GA}{GH}=\frac{GA^2}{2GH}\)
Ta có :
\(GH=\frac{AA'}{3}=\frac{a}{2};AH=\frac{a\sqrt{3}}{3};GA^2=GH^2+AH^2=\frac{7a^2}{12}\)
Do đó \(R=\frac{7a^2}{2.12}.\frac{2}{a}=\frac{7a}{12}\)
Đúng 0
Bình luận (1)
Cho lăng trụ
A
B
C
D
.
A
B
C
D
có đáy là hình vuông cạnh
a
3
. Hình chiếu vuông góc của điểm A lên mặt phẳng
(
A
B
C
D
)
trùng với tâm O của hình vuông
A
B
C
D
. Biết rằng...
Đọc tiếp
Cho lăng trụ A B C D . A ' B ' C ' D ' có đáy là hình vuông cạnh a 3 . Hình chiếu vuông góc của điểm A lên mặt phẳng ( A ' B ' C ' D ' ) trùng với tâm O của hình vuông A ' B ' C ' D ' . Biết rằng khoảng cách từ trọng tâm G của tam giác AB’D’ đến mặt phẳng (AA’D) bằng a 2 . Khoảng cách từ điểm O đến mặt phẳng ( A D C ' B ' ) bằng
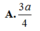

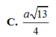
![]()
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi O là tâm của mặt đáy ABCD.
a) Chứng minh O.A'B'C'D' là hình chóp tứ giác đều.
b) Gọi thể tích hình chóp đều O.A'B’C'D' là V' và thể tích hình lập phương là V. Tính tỉ số V'/V
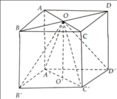
a) Bốn tam giác OAA', OBB', OCC', ODD' là các tam giác vuông bằng nhau nên suy ra OA' = OB' = OC' = OD'.
Hình chóp O.A'B'C'D' là hình chóp đều vì có các mặt bên là tam giác cân và đáy là đa giác đều.
b) Thể tích của của hình chóp O.A'B'C'D' là:
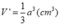
Thể tích hình lập phương:
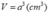
Vậy V ' V = 1 3
Đúng 0
Bình luận (0)
Cho hình lăng trụ tam giác ABC A'B'C'. Gọi K M N E lần lượt là trung điểm của các cạnh CC' AB AA' và BB' . G là trọng tâm tam giác ABC, I là điểm thuộc đoạn BC sao cho BI = 1/3 BC. CMR
a/ (MNC) // (A'BK)
b/ (MNK) // (A'BC')
c/ ( GKN) // (A'IC')
Giúp mình câu c với ạ
Cho hình lập phương ABCD.ABCD cạnh a. Gọi S là tâm ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.a) Chứng minh S.MNPQ là hình chóp tứ giác đều.b) Gọi thể tích hình chóp S.MNPQ là V và thể tích hình lập phương là V. Tính tỉ số V/V
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi S là tâm A'B'C'D'. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh S.MNPQ là hình chóp tứ giác đều.
b) Gọi thể tích hình chóp S.MNPQ là V' và thể tích hình lập phương là V. Tính tỉ số V'/V
Tương tự 2A.
a) Hình chóp S.MNPQ là hình chóp đều vì các mặt bên là tam giác cân và đáy MNPQ là đa giác đều.
b)
V
'
V
=
1
6
. Chú ý 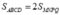
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.ABCD có cạnh bằng
2
a
2
Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.ABCD Khi đó
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2 a 2 Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.A'B'C'D' Khi đó
![]()
![]()
![]()
![]()
Cho hình lập phương ABCD.ABCD có cạnh bằng
2
a
2
. Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.ABCD. Khi đó
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2 a 2 . Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.A'B'C'D'. Khi đó
![]()
![]()
![]()
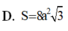
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng
2
a
2
.
Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương
A
B
C
D
.
A
B
C
D
Khi đó A.
S...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng 2 a 2 . Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương A B C D . A ' B ' C ' D ' Khi đó
A. S = 4 a 2 3
B. S = 8 a 2
C. S = 16 a 2 3
D. S = 8 a 2 3
Đáp án D
Cạnh của bát diện đều là x = 2 a → S = 8. 2 a 2 3 4 = 8 a 2 3
Đúng 0
Bình luận (0)










