Cho hình thang ABCD đường cao AH. Có S=6C0cm vuông,AH=5cm,cạnh AB=3cm.Tìm cạnh DC

Những câu hỏi liên quan
Bài 7: Cho hình thang cân ABCD (AB//CD ) , DC là đáy lớn AH là đường cao , M; N là trung điểm hai cạnh bên AD và BC . a) Chứng minh MNCH là hình bình hành b) Nếu AH=5cm . Tính đường trung bình của hình thang ABCD trên
cho hình thang cân ABCD có AB//CD và AB<CD, đường chéo BD vuông góc với cạnh BC. vẽ đường cao AH
a) CM tam giác BDC đồng dạng với tam giác HBC
b) Cho BC=15cm, DC=25cm. tính HC,HD
c) tính S abcd
Sửa đề: Đường cao BH
a: Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔBDC\(\sim\)ΔHBC
b: Áp dụng định lí Pytago vào ΔBDC vuông tại B, ta được:
\(DC^2=BD^2+BC^2\)
\(\Leftrightarrow BD^2=25^2-15^2=400\)
hay BD=20(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBDC vuông tại B có BH là đường cao ứng với cạnh huyền DC, ta được:
\(\left\{{}\begin{matrix}BD^2=HD\cdot DC\\BC^2=HC\cdot DC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}HD=16\left(cm\right)\\HC=9\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Câu 1: Vẽ ΔABC có góc B=120 độ, AB=3cm, BC=6cm.Vẽ đường cao AH và trung tuyến AM của ΔABC
Câu 2:Cho hình thang vuông ABCD: AB // CD, góc A= góc D=90 độ;Cạnh đáy AB=4cm;Cạnh đáy DC=5cm;Cạnh bên AD=3cm.Gọi M,N,P,Q là trung điểm của AB, BC, CD và AD
a)MNPQ là hình gì ? Vì sao
b)Tính MQ, MN,BC ?
MÌNH CẦN GẤP Ạ!!!!!!
1, Cho hình thang cân ABCD có đáy nhỏ AB, đường cao AH=2cm. Biết HC=3,5cm và HD=1,5cm. Tính chu vi của hình thang này 2, Cho hình thang cân ABCD có cạnh bên AD=5cm, các cạnh đáy AB=6cm và CD=14cm. Tính chiều cao của hình thang. XIN HÃY GIÚP MÌNH Ạ, xin cảm ơn 🌹❤️
1/ cho tam giác ABC vuông tại A , có đường cao AH , phân giác AD biết BD15cm Dc20cm Tính AH,AD làm tròn đến chữ số thập phân thứ 2 2/cho tam giác ABC vuông tại A ,đường cao AH ,Trung tuyến AM a) Biết BC125cm , AB phần AC 3 phần 4 Tính độ dài hình chiếu của mỗi cạnh góc vuông trên cạnh huyền b) Biết AH42cm , AB:AC3:7 .Tính độ dài hình chiếu của mỗi cạnh góc vuông trên cạnh huyền c) Biết AH48cm , HB:HC9:16 tính AB,AC,BC d) Biết AH:AM40:41 Tính tỉ số AB phần Ac 3/Hình thang ABCD có AB//CD và hai đ...
Đọc tiếp
1/ cho tam giác ABC vuông tại A , có đường cao AH , phân giác AD biết BD=15cm Dc=20cm
Tính AH,AD làm tròn đến chữ số thập phân thứ 2
2/cho tam giác ABC vuông tại A ,đường cao AH ,Trung tuyến AM
a) Biết BC=125cm , AB phần AC = 3 phần 4 Tính độ dài hình chiếu của mỗi cạnh góc vuông trên cạnh huyền
b) Biết AH=42cm , AB:AC=3:7 .Tính độ dài hình chiếu của mỗi cạnh góc vuông trên cạnh huyền
c) Biết AH=48cm , HB:HC=9:16 tính AB,AC,BC
d) Biết AH:AM=40:41 Tính tỉ số AB phần Ac
3/Hình thang ABCD có AB//CD và hai đường chéo vuông góc . Biết BD=15cm và dường cao hình thang bằng 12cm .Tính diện tích hình thang ABCD
4/Cho tam giác ABC cân tại A có đường cao AH=32cm đường cao BK=38,4 cm
a) tính các cạnh của tam giác ABC
b) đường trung trục của AC cắt AH tai O tính OH
Cho hình bình hàng ABCD (AB//CD), DC là đáy lớn AH là đường cao, M,N là trung điểm hai cạnh bên AD và BC
a) Chứng minh MNCH là hình bình hàng
b) Nếu DH = 5cm, AB = 10cm
Tính đường trung bình của hình thang ABCD trên
a) Ta có MN là đường trung bình của tam giác ABD, do đó MN song song với AB và có độ dài bằng một nửa độ dài AB.
Tương tự, MN song song với CD và có độ dài bằng một nửa độ dài CD.
Vì AB//CD, nên MN song song với AB và CD.
Do đó, ta có MNCH là hình bình hành.
*Ib có phần b nhé =))
Đúng 0
Bình luận (0)
Cho hình thang ABCD đáy lớn DC bằng 10cm,đáy bé AB = 6cm,đường cao AH = 5cm . Trên cạnh BC lấy điểm M sao cho BC=3xBM.Hãy tính diện tích tứ giác AMCD
Cho hình thang ABCD, đường cao ứng với cạnh DC là AH = 6cm; cạnh DC = 12cm. Diện tích của hình bình hành ABCD là:
A. 72 c m 2
B. 82 c m 2
C. 92 c m 2
D. 102 c m 2
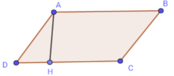
Ta có: SABCD = AH.CD = 6.12 = 72(cm2)
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD đáy nhỏ AB = 4cm, đáy lớn CD = 10cm, cạnh bên BC = 5cm thì đường cao AH bằng:
A. 4,5 cm.
B. 4 cm.
C. 3,5 cm.
D. 3 cm.
Đáp án cần chọn là: B

Kẻ BK ⊥ DC tại K.
Vì ABCD là hình thang cân nên ta có D ^ = C ^ ; AD = BC
=> ΔAHD = ΔBKC (ch – gn) => DH = CK
Suy ra DH = 1 2 (CD – AB)
Suy ra DH = 1 2 (CD – AB) = 1 2 (10 – 4)
Do ABCD là hình thang cân nên AD = BC = 5 cm
Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có
A D 2 = A H 2 + D H 2 ⇒ A H 2 = A D 2 - D H 2 = 5 2 - 3 2 ⇒ A H = 4
Vậy AH = 4cm.
Đúng 1
Bình luận (0)













