cho tâm giác ABC đều nội tiếp đường tròn (O) . D là điểm di động trên cung BC trên AD lấy điểm M sao cho DB=DM . chứng minh điểm M thuộc một đường có định
Những câu hỏi liên quan
Cho tam giác ABC đều nội tiếp đường tròn (O), D là điểm di động trên cung BC. Trên AD lấy điểm M sao cjo DB=DM. Chứng minh: Điểm M thuộc một đường cố định
Cho tam giác ABC đều nội tiếp đường tròn tâm o. Điểm D di động trên cung BC. Trên AD lấy điểm M sao choDB=DM .CM điểm M thuộc 1 đường cố định
Trả lời nhanh jup mk
cho tâm giác ABC đều nội tiếp đường tròn (O) . D là điểm di động trên cung BC trên AD lấy điểm M sao cho DB=DM . chứng minh điểm M thuộc một đường có định
Cho tam giác ABC nội tiếp đường tròn (O). P di chuyển trên cung
B
C
⏜
chứa A của (O). I là tâm đường tròn nội tiếp tam giác ABC. Q là tâm đường tròn nội tiếp tam giác PBC.1). Chứng minh rằng B, I, Q, C cùng nằm trên một đường tròn.2) Trên tia BQ, CQ lần lượt lấy các điểm M, N sao cho
B
M
B
I
,
C
N
C
I
. Chứng m...
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O). P di chuyển trên cung B C ⏜ chứa A của (O).
I là tâm đường tròn nội tiếp tam giác ABC. Q là tâm đường tròn nội tiếp tam giác PBC.
1). Chứng minh rằng B, I, Q, C cùng nằm trên một đường tròn.
2) Trên tia BQ, CQ lần lượt lấy các điểm M, N sao cho B M = B I , C N = C I . Chứng minh rằng MN luôn đi qua một điểm cố định.
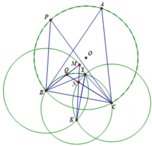
1) Ta có
B I C ^ = 180 0 − I B C ^ − I C B ^ = 180 0 − A B C ^ 2 − A C B ^ 2 = 180 0 − 180 ∘ − B A C ^ 2 = 90 0 + B A C ^ 2 ⇔ B A C ^ = 2 B I C ^ − 180 °
Tương tự B Q C ^ = 90 0 + B P C ^ 2 ⇔ B P C ^ = 2 B Q C ^ − 180 ° .
Tứ giác BPAC nội tiếp, suy ra B A C ^ = B P C ^ ⇒ B Q C ^ = B I C ^ , nên 4 điểm B, I, Q, C thuộc một đường tròn.
2) Gọi đường tròn (B; BI) giao (C; CI) tại K khác I thì K cố định.
Góc I B M ^ là góc ở tâm chắn cung I M ⏜ và I K M ^ là góc nội tiếp chắn cung I M ⏜ , suy ra I K M ^ = 1 2 I B M ^ (1).
Tương tự I K N ^ = 1 2 I C N ^ (2).
Theo câu 1) B, I, Q, C thuộc một đường tròn, suy ra I B M ^ = I B Q ^ = I C Q ^ = I C N ^ (3).
Từ (1), (2) và (3), suy ra I K M ^ = I K N ^ ⇒ K M ≡ K N .
Vậy MN đi qua K cố định.
Đúng 0
Bình luận (0)
1) Cho đường tròn (O) đường kính AB 2R. Lấy điểm C di động trên đường tròn (O), gọi I là tâm đường tròn nội tiếp tam giác ABC, vẽ CH vuông góc AB tại H. a) Vẽ CM song song BI ( M thuôc đường thẳng AI). Trên đoạn thẳng AB lấy điểm F sao cho AC AF. Tính số đo góc CMF.b) Gọi K là tâm đường tròn nội tiếp tam giác CHA, CK cắt AB tại E. Tính giá trị lớn nhất của diện tích tam giác CEF theo R khi C di động trên (O). c) Chứng minh ba đường thẳng MH, CF và BI đồng qui tại một điểm.2) Cho tam giác nhọn...
Đọc tiếp
1) Cho đường tròn (O) đường kính AB = 2R. Lấy điểm C di động trên đường tròn (O), gọi I là tâm đường tròn nội tiếp tam giác ABC, vẽ CH vuông góc AB tại H.
a) Vẽ CM song song BI ( M thuôc đường thẳng AI). Trên đoạn thẳng AB lấy điểm F sao cho AC = AF. Tính số đo góc CMF.
b) Gọi K là tâm đường tròn nội tiếp tam giác CHA, CK cắt AB tại E. Tính giá trị lớn nhất của diện tích tam giác CEF theo R khi C di động trên (O).
c) Chứng minh ba đường thẳng MH, CF và BI đồng qui tại một điểm.
2) Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O;R). Gọi M là điểm di động trên cung nhỏ BC. Vẽ AD vuông góc với MB tại D, AE vuông góc với MC tại E. Gọi H là giao điểm của DE và BC.
a) Chứng minh A, H,E cùng thuộc một đường tròn. Từ đó suy ra DE luôn đi qua một điểm cố định.
b) Xác định vị trí của M để MB/AD×MC/AE đạt giá trị lớn nhất.
Mọi người giúp em với ạ.
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm (O). Trên cạnh BC lấy điểm D sao cho đường thẳng vuông góc với BC tại D cắt cung nhỏ AC tại đường tròn tâm (O) tại M. Gọi E là hình chiếu của M trên AC.
a) Chứng minh tứ giác CDEM nội tiếp một đường tròn.
b) Chứng minh: MA.MD=MB.ME.
a: góc CDM=góc CEM=90 độ
=>CDEM nội tiếp
b: Xet ΔMEA vuông tại E và ΔMDB vuông tại D có
góc EMA chung
=>ΔMEA đồng dạng với ΔMDB
=>ME/MD=MA/MB
=>ME*MB=MA*MD
Đúng 0
Bình luận (0)
a. góc CDM=góc CEM=90 độ
=>CDEM nội tiếp
b. Xet ΔMEA vuông tại E và ΔMDB vuông tại D có
góc EMA chung
=>ΔMEA đồng dạng với ΔMDB
=>ME/MD=MA/MB
=>ME*MB=MA*MD
Đúng 0
Bình luận (0)
cho đường tròn (O;R) có BC là dây cố định (BC2R) ; E là điểm chính giữa cung nhỏ BC. gọi A là điểm di động trên cung lớn BC và ABAC (A khác B). trên đoạn AC lấy điểm D khác C sao cho EDEC. tia BD cắt đường tròn (O;R) tại điểm thứ hai là F. a) chứng minh D là trực tâm của tam giác AEF. b) gọi H là trực tâm tam giác DEC ; DH cắt BC tại N. đường tròn ngoại tiếp tam giác BDN cắt đường tròn (O;R) tại điểm thứ hai là M. chứng minh đường thẳng DM luôn đi qua một điểm cố định.
Đọc tiếp
cho đường tròn (O;R) có BC là dây cố định (BC<2R) ; E là điểm chính giữa cung nhỏ BC. gọi A là điểm di động trên cung lớn BC và AB<AC (A khác B). trên đoạn AC lấy điểm D khác C sao cho ED=EC. tia BD cắt đường tròn (O;R) tại điểm thứ hai là F.
a) chứng minh D là trực tâm của tam giác AEF.
b) gọi H là trực tâm tam giác DEC ; DH cắt BC tại N. đường tròn ngoại tiếp tam giác BDN cắt đường tròn (O;R) tại điểm thứ hai là M. chứng minh đường thẳng DM luôn đi qua một điểm cố định.
a) Bổ đề: Xét tam giác ABC cân tại A, một điểm M bất kì sao cho ^AMB = ^AMC. Khi đó MB = MC.
Bổ đề chứng minh rất đơn giản, không trình bày ở đây.
Áp dụng vào bài toán: Vì E là điểm chính giữa (BC nên EB = EC = ED => \(\Delta\)BED cân tại E
Ta có ^BAE = ^CAE (2 góc nội tiếp chắn hai cung bằng nhau) hay ^BAE = ^DAE
Áp dụng bổ đề vào \(\Delta\)BED ta được AB = AD. Khi đó AE là trung trực của BD => AE vuông góc BD
Lại có \(\Delta\)BAD ~ \(\Delta\)CFD (g.g). Mà AB = AD nên FD =FC. Từ đó EF vuông góc DC
Xét \(\Delta\)AEF có FD vuông góc AE (cmt), AD vuông góc EF (cmt) => D là trực tâm \(\Delta\)AEF (đpcm).
b) Gọi DN cắt EC tại I. Ta dễ thấy ^MDI = ^MDN = ^MBN = ^MBC = ^MEC = ^MEI
Suy ra bốn điểm D,E,M,I cùng thuộc một đường tròn => ^EMD = ^EID = 900
Nếu ta gọi MD cắt cung lớn BC của (O) tại S thì ^EMS chắn nửa (O) hay ES là đường kính của (O)
Mà E là điểm chính giữa cung nhỏ BC nên S là điểm chính giữa cung lớn BC
Do đó S là điểm cố định (Vì B,C cố định). Vậy MD luôn đi qua S cố định (đpcm).
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O , đường kính AI điểm M tùy ý trên cung nhỏ AC(M khác A, M khác C) .Kẻ tia Mx là tia đối của tia MC .1) Trên tia đối của tia MB lấy điểm D sao cho MD MC, Gọi K là giao điểm thứ hai của DC với đường tròn tâm O . chứng minh rằng tứ giác MIKD là hình bình hành3) Chứng minh rằng khi M di động trên cung nhỏ AC thì D di động trên cung tròn cố định
Đọc tiếp
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O , đường kính AI điểm M tùy ý trên cung nhỏ AC(M khác A, M khác C) .Kẻ tia Mx là tia đối của tia MC .
1) Trên tia đối của tia MB lấy điểm D sao cho MD= MC, Gọi K là giao điểm thứ hai của DC với đường tròn tâm O . chứng minh rằng tứ giác MIKD là hình bình hành
3) Chứng minh rằng khi M di động trên cung nhỏ AC thì D di động trên cung tròn cố định
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O đường kính AI điểm M tùy ý trên cung nhỏ ACq(Mkhác A,M khác C)kẻ tia Mx là tia đối của tia MC.A)Trên tia đối của tia MB lấy điểm D sao cho MD MC, Gọi K là giao điểm thứ hai của DC với đường tròn tâm O .chứng minh rằng tứ giác MIKD là hình bình hànhB) Chứng minh rằng khi M di động trên cung nhỏ AC thì D di động trên cung tròn cố định
Đọc tiếp
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O đường kính AI điểm M tùy ý trên cung nhỏ ACq(Mkhác A,M khác C)kẻ tia Mx là tia đối của tia MC.
A)Trên tia đối của tia MB lấy điểm D sao cho MD= MC, Gọi K là giao điểm thứ hai của DC với đường tròn tâm O .chứng minh rằng tứ giác MIKD là hình bình hành
B) Chứng minh rằng khi M di động trên cung nhỏ AC thì D di động trên cung tròn cố định