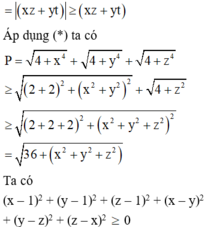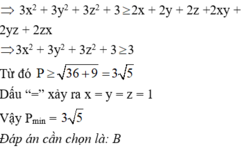x2 +y2+z2=xy+yz+zx với x+y+z=6

Những câu hỏi liên quan
cho các số thực dưong x,y,z thỏa mãn : x2+y2+z2=3
chứng minh rằng : \(\dfrac{x}{\sqrt[3]{yz}}+\dfrac{y}{\sqrt[3]{zx}}+\dfrac{z}{\sqrt[3]{xy}}\ge xy+yz+zx\)
nhờ mn giúp mk bài này vs ạ
mk đang cần gấp !
cảm ơn mn nhiều
Đúng 0
Bình luận (0)
Đặt \(\left(\sqrt[3]{x};\sqrt[3]{y};\sqrt[3]{z}\right)=\left(a;b;c\right)\) \(\Rightarrow a^6+b^6+c^6=3\)
\(a^6+a^6+a^6+a^6+a^6+1\ge6a^5\)
Tương tự: \(5b^6+1\ge6b^5\) ; \(5c^6+1\ge6c^5\)
Cộng vế với vế: \(18=5\left(a^6+b^6+c^6\right)+3\ge6\left(a^5+b^5+c^5\right)\)
\(\Rightarrow3\ge a^5+b^6+b^5\)
BĐT cần chứng minh: \(\dfrac{a^3}{bc}+\dfrac{b^3}{ca}+\dfrac{c^3}{ab}\ge a^3b^3+b^3c^3+c^3a^3\)
Ta có:
\(\dfrac{a^3}{bc}+\dfrac{b^3}{ca}+\dfrac{c^3}{ab}\ge\dfrac{ab}{c}+\dfrac{bc}{a}+\dfrac{ca}{b}\ge a+b+c\) (1)
Mà \(3\left(a+b+c\right)\ge\left(a^5+b^5+c^5\right)\left(a+b+c\right)\ge\left(a^3+b^3+c^3\right)^2\ge3\left(a^3b^3+b^3c^3+c^3a^3\right)\)
\(\Rightarrow a+b+c\ge a^3b^3+b^3c^3+c^3a^3\) (2)
Từ (1);(2) \(\Rightarrow\) đpcm
Đúng 2
Bình luận (1)
Cho x,y,z >0 t/m x2+y2+z2=3.
C/m \(\dfrac{x}{\sqrt[3]{yz}}+\dfrac{y}{\sqrt[3]{xz}}+\dfrac{z}{\sqrt[3]{xy}}\ge xy+yz+zx\)
Bạn tham khảo lời giải tại đây:
cho các số thực dưong x,y,z thỏa mãn : x2 y2 z2=3chứng minh rằng : \(\dfrac{x}{\sqrt[3]{yz}} \dfrac{y}{\sqrt[3]{zx}} \df... - Hoc24
Đúng 0
Bình luận (0)
Cách khác:
Áp dụng BĐT AM-GM và BĐT Cauchy-Schwarz:
\(\sum \frac{x}{\sqrt[3]{yz}}\geq \sum \frac{x}{\frac{y+z+1}{3}}=3\sum \frac{x}{y+z+1}=3\sum \frac{x^2}{xy+xz+x}\)
\(\geq 3. \frac{(x+y+z)^2}{2(xy+yz+xz)+(x+y+z)}\)
Ta sẽ chứng minh: \(\frac{3(x+y+z)^2}{2(xy+yz+xz)+(x+y+z)}\geq xy+yz+xz(*)\)
Đặt $x+y+z=a$ thì $xy+yz+xz=\frac{a^2-3}{2}$
Bằng BĐT AM-GM dễ thấy $\sqrt{3}< a\leq 3$
BĐT $(*)$ trở thành:
$\frac{3a^2}{a^2+a-3}\geq \frac{a^2-3}{2}$
$\Leftrightarrow a^4+a^3-12a^2-3a+9\leq 0$
$\Leftrightarrow (a-3)(a+1)(a^2+3a-3)\leq 0$
Điều này đúng với mọi $\sqrt{3}< a\leq 3$
Do đó BĐT $(*)$ đúng nên ta có đpcm.
Dấu "=" xảy ra khi $x=y=z=1$
Đúng 0
Bình luận (0)
phân tích a)(x-y)3+(y-z)3+(z-x)3
b)x.(y2-z2)+y.(z2-x2)+z.(x2-y2)
c)xy.(x-y)-xz.(x+z)-yz.(zx-y+z)
d)x.(y+z)2+y.(z-x)2+z.(x+y)2-4xyz
a)(x-y)3+(y-z)3+(z-x)3
=3(x-y+y-z+z-x)=3
b)nhân vào là rồi đối trừ là hết luôn ( nhưng là mũ 2 hay nhân 2 v mk là theo nhân 2 nhé]
Đúng 0
Bình luận (0)
Cho 1/x + 1/y + 1/z = 0. Tính N = yz/x2 + zx/y2 + xy/z2
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\\ \Rightarrow\left\{{}\begin{matrix}1+\dfrac{x}{y}+\dfrac{x}{z}=0\\\dfrac{y}{x}+1+\dfrac{y}{z}=0\\\dfrac{z}{x}+\dfrac{z}{y}+1=0\end{matrix}\right.\\ \Rightarrow\dfrac{x}{y}+\dfrac{x}{z}+\dfrac{y}{x}+\dfrac{y}{z}+\dfrac{z}{x}+\dfrac{z}{y}=-3\)
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\\ \Rightarrow\dfrac{yz+xz+xy}{xyz}=0\\ \Rightarrow yz+xz+xy=0\)
\(\Rightarrow\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}\right)\left(xy+xz+yz\right)=0\\ \Rightarrow\dfrac{yz}{x^2}+\dfrac{xz}{y^2}+\dfrac{xy}{z^2}+\dfrac{x}{y}+\dfrac{x}{z}+\dfrac{y}{x}+\dfrac{y}{z}+\dfrac{z}{x}+\dfrac{z}{y}=0\\ \Rightarrow\dfrac{yz}{x^2}+\dfrac{xz}{y^2}+\dfrac{xy}{z^2}=3\)
Đúng 0
Bình luận (2)
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\)
\(\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{-1}{z}\)
\(\Rightarrow\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^3=\left(\dfrac{-1}{z}\right)^3\)
\(\Leftrightarrow\dfrac{1}{x^3}+3\dfrac{1}{x^2}\dfrac{1}{y}+3\dfrac{1}{x}\dfrac{1}{y^2}+\dfrac{1}{y^3}=\dfrac{-1}{z^3}\)
\(\Leftrightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=-3.\dfrac{1}{x}\dfrac{1}{y}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\)
\(\Leftrightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=-3\dfrac{1}{x}\dfrac{1}{y}\dfrac{-1}{z}\)
\(\Leftrightarrow\left(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}\right)xyz=3\dfrac{1}{x}\dfrac{1}{y}\dfrac{1}{z}.xyz\)
\(\Leftrightarrow\dfrac{yz}{x^2}+\dfrac{xz}{y^2}+\dfrac{xy}{z^2}=3\)
Đúng 7
Bình luận (1)
Vì 1/x + 1/y + 1/z = 0 nên lần lượt nhân vs x; y; z ta có:
1 + x/y + x/z = 0 (1)
1 + y/z + y/x = 0 (2)
1 + z/x + z/y = 0 (3)
Từ (1); (2); (3) suy ra : x/y + y/z + z/x + x/z + y/x + z/y = - 3 (*)
Mặt khác : 1/x + 1/y + 1/z = 0 nên quy đồng lên ta có:
(xy + yz + zx)/xyz = 0 hay xy + yz + zx = 0
Hay : (1/x^2 + 1/y^2 + 1/z^2).(xy + yz + zx) = 0
khai triển ra :
yz/x^2 + zx/y^2 + xy/z^2 + x/y + y/z + z/x + x/z + y/x + z/y = 0
Vậy : yz/x^2 + zx/y^2 + xy/z^2 = - (x/y + y/z + z/x + x/z + y/x + z/y) = 3 (theo (*))
Đúng 0
Bình luận (0)
Cho 1/x + 1/y + 1/z = 0. Tính N = yz/x2 + zx/y2 + xy/z2
Ta có : \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0< =>\frac{xyz}{x}+\frac{xyz}{y}+\frac{xyz}{z}=0< =>xy+yz+zx=0\)
Suy ra \(\left(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}\right)\left(xy+yz+zx\right)=0< =>\frac{y}{x}+\frac{yz}{x^2}+\frac{z}{x}+\frac{x}{y}+\frac{z}{y}+\frac{zx}{y^2}+\frac{xy}{z}+\frac{y}{z}+\frac{x}{z}=0\)
\(< =>N+\frac{z}{x}+\frac{z}{y}+\frac{y}{x}+\frac{y}{z}+\frac{x}{y}+\frac{x}{z}=0< =>N+z\left(-\frac{1}{z}\right)+y\left(-\frac{1}{y}\right)+x\left(-\frac{1}{x}\right)=0\)
\(< =>N-1-1-1=0< =>N-3=0< =>N=3\)
Vậy \(N=\frac{xy}{z^2}+\frac{yz}{x^2}+\frac{zx}{y^2}=3\)
x,y,z >o ; x2+y2+z2 = 3 ( x mũ hai , y mũ hai , z mũ hai nha )
C/m xy/z + yz/x+ zx/y lớn hơn hoặc bằng 3
Đặt \(\left(\frac{yz}{x};\frac{zx}{y};\frac{xy}{z}\right)=\left(a;b;c\right)\Rightarrow ab+bc+ca=x^2+y^2+z^2=3\)
Ta có:
\(a+b+c\ge\sqrt{3\left(ab+bc+ca\right)}=\sqrt{9}=3\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\) hay \(x=y=z=1\)
Đúng 0
Bình luận (0)
Với x; y; z là các số thực thỏa mãn x + y + z + xy + yz + zx 6. Tìm giá trị nhỏ nhất của biểu thức:
P
4
+
x
4
+
4
+
y
2
+
4
+
z
2
A.
P
min
5...
Đọc tiếp
Với x; y; z là các số thực thỏa mãn x + y + z + xy + yz + zx = 6. Tìm giá trị nhỏ nhất của biểu thức: P = 4 + x 4 + 4 + y 2 + 4 + z 2
A. P min = 5
B. P min = 3 5
C. P min = 5 3
D. P min = 3
cho x y z là các số thực dương thỏa mãn x + y + z = 3.Tìm GTLN của A= xy/căn(z2+3) + yz/căn(x2+3) + zx/căn(y2+3)
Chứng minh các bất đẳng thức sau với x, y, z 0a) x2 + y2 ≥ (x + y)2/2b) x3 + y3 ≥ (x + y)3/4c) x4 + y4 ≥ (x + y)4/8d) x2 + y2 + z2 ≥ xy + yz + zxe) x2 + y2 + z2 ≥ (x + y + z)2/3f) x3 + y3 + z3 ≥ 3xyz
Đọc tiếp
Chứng minh các bất đẳng thức sau với x, y, z > 0
a) x2 + y2 ≥ (x + y)2/2
b) x3 + y3 ≥ (x + y)3/4
c) x4 + y4 ≥ (x + y)4/8
d) x2 + y2 + z2 ≥ xy + yz + zx
e) x2 + y2 + z2 ≥ (x + y + z)2/3
f) x3 + y3 + z3 ≥ 3xyz
a: Ta có: \(\left(x+y\right)^2\)
\(=x^2+2xy+y^2\)
\(\Leftrightarrow x^2+y^2=\dfrac{\left(x+y\right)^2}{2xy}\ge\dfrac{\left(x+y\right)^2}{2}\forall x,y>0\)
Đúng 1
Bình luận (0)
1). x2y2(y-x)+y2z2(z-y)-z2x2(z-x)
2)xyz-(xy+yz+xz)+(x+y+z)-1
3)yz(y+z)+xz(z-x)-xy(x+y)
4)2a2b+4ab2-a2c+ac2-4b2c+2bc2-4abc
5)y(x-2z)2+8xyz+x(y-2z)2-2z(x+y)2
6)8x3(y+z)-y3(z+2x)-z3(2x-y)
7) (x2+y2)3+(z2-x2)3-(y2+z2)3