a2+2ab+b2-2a-2b+1

Những câu hỏi liên quan
Địa chỉ ô được viết như sau?
A. A2+B2 B. 2A + 2B C. 2,A + 2,B D. 2AB + 2 BA
Xem thêm câu trả lời
Tìm giá trị nhỏ nhất của:
N=a2+b2+2a-b-\(\dfrac{1}{4}\)
P=a2+2a-4ab+5b2-2b-10
a) Ta có: \(N=a^2+b^2+2a-b-\dfrac{1}{4}\)
\(=a^2+2a+1+b^2-b+\dfrac{1}{4}-\dfrac{3}{2}\)
\(=\left(a+1\right)^2+\left(b-\dfrac{1}{2}\right)^2-\dfrac{3}{2}\ge-\dfrac{3}{2}\forall a,b\)
Dấu '=' xảy ra khi a=-1 và \(b=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của:
N=a2+b2+2a-b\(-\dfrac{1}{4}\)
P=a2+2a-4ab+5b2-2b-10
a) Ta có: \(N=a^2+b^2+2a-b-\dfrac{1}{4}\)
\(=a^2+2a+1+b^2-b+\dfrac{1}{4}-\dfrac{3}{2}\)
\(=\left(a+1\right)^2+\left(b-\dfrac{1}{2}\right)^2-\dfrac{3}{2}\ge-\dfrac{3}{2}\forall a,b\)
Dấu '=' xảy ra khi a=-1 và \(b=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức (a+b/b-2b/b-a).b-a/a2+b2+(a2+1/2a-1-a/2):a+2/1-2a
a, cho a=+b+c =1; a,b,c dương
tìm GTNN: A= a/b2+1 + b/c2+1 + c/a2+1
b, cho a,b,c dương có tổng =2
tìm GTNN; B= a/ab+2c + b/bc+2a + c/ca+2b
c, cho a,b,c dương và a+b+c<1
tìm GTNN: C= 1/a2+2bc + 1/ b2+2ac + 1/c2+2ab
Phân tích các đa thức sau thành nhân tử: a) x2 - 9 - x2 (x2 - 9) d) x2 + 5x + 6 h) a2 + b2 + 2a – 2b – 2ab b) x2(x-y) + y2(y-x) e) 3x2 – 4x – 4 i) (x + 1)2 – 2(x + 1)(y – 3) + (y – 3)2c) x3+27+(x+3)(x-9) g) x4 + 64y4 k) x2(x + 1) – 2x(x + 1) + x + 1Mình đang cần gấp ạ
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
a) x2 - 9 - x2 (x2 - 9) d) x2 + 5x + 6 h) a2 + b2 + 2a – 2b – 2ab
b) x2(x-y) + y2(y-x) e) 3x2 – 4x – 4 i) (x + 1)2 – 2(x + 1)(y – 3) + (y – 3)2
c) x3+27+(x+3)(x-9) g) x4 + 64y4 k) x2(x + 1) – 2x(x + 1) + x + 1
Mình đang cần gấp ạ
a: \(x^2-9-x^2\left(x^2-9\right)\)
\(=\left(x^2-9\right)-x^2\left(x^2-9\right)\)
\(=\left(x^2-9\right)\left(1-x^2\right)\)
\(=\left(1-x\right)\left(1+x\right)\left(x-3\right)\left(x+3\right)\)
b: \(x^2\left(x-y\right)+y^2\left(y-x\right)\)
\(=x^2\left(x-y\right)-y^2\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2-y^2\right)\)
\(=\left(x-y\right)\left(x-y\right)\left(x+y\right)=\left(x-y\right)^2\cdot\left(x+y\right)\)
c: \(x^3+27+\left(x+3\right)\left(x-9\right)\)
\(=\left(x+3\right)\left(x^2-3x+9\right)+\left(x+3\right)\left(x-9\right)\)
\(=\left(x+3\right)\left(x^2-3x+9+x-9\right)\)
\(=\left(x+3\right)\left(x^2-2x\right)=x\left(x-2\right)\left(x+3\right)\)
d: \(x^2+5x+6\)
\(=x^2+2x+3x+6\)
\(=x\left(x+2\right)+3\left(x+2\right)=\left(x+2\right)\left(x+3\right)\)
e: \(3x^2-4x-4\)
\(=3x^2-6x+2x-4\)
\(=3x\left(x-2\right)+2\left(x-2\right)\)
\(=\left(x-2\right)\left(3x+2\right)\)
g: \(x^4+64y^4\)
\(=x^4+16x^2y^2+64y^4-16x^2y^2\)
\(=\left(x^2+8y^2\right)^2-\left(4xy\right)^2\)
\(=\left(x^2+8y^2-4xy\right)\left(x^2+8y^2+4xy\right)\)
Đúng 1
Bình luận (0)
h: \(a^2+b^2+2a-2b-2ab\)
\(=a^2-2ab+b^2+2a-2b\)
\(=\left(a-b\right)^2+2\left(a-b\right)=\left(a-b\right)\left(a-b+2\right)\)
i: \(\left(x+1\right)^2-2\left(x+1\right)\left(y-3\right)+\left(y-3\right)^2\)
\(=\left(x+1-y+3\right)^2\)
\(=\left(x-y+4\right)^2\)
k: \(x^2\left(x+1\right)-2x\left(x+1\right)+\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-2x+1\right)\)
\(=\left(x+1\right)\left(x-1\right)^2\)
Đúng 1
Bình luận (0)
Tính giá trị biểu thức:a) M (a - 2b)(
a
2
+ 2ab + 4
b
2
) +
(
2
b
-
a
)
3
tại a -1; b 2;b) N (2xy - 2)(2xy + 3) -
(
1
-
...
Đọc tiếp
Tính giá trị biểu thức:
a) M = (a - 2b)( a 2 + 2ab + 4 b 2 ) + ( 2 b - a ) 3 tại a = -1; b = 2;
b) N = (2xy - 2)(2xy + 3) - ( 1 - 2 xy ) 2 tại x = 1 2 ; y = -1.
a) Rút gọn M = -6ab(-2b + a). Tính được M = 60.
b) Rút gọn M = 6xy – 7. Tính được N = -10.
Đúng 0
Bình luận (0)
11,18y2 - 12xy + 2x2 12,(x2+x)2 + 3(x2+x) + 213,5x2 - 10xy + 5y2 - 20z2 14,x3 - 9x + 2x2 - 1815,x2 - 2x - 4y2 - 4y16,a2 + 2ab + b2 - 2a - 2b + 117,x3 - x + 3x2 y + 3xy2 + y3 - y 18,x3 + y3 + z3 - 3xyz19,x2 + 4x - 520,2x2 - 6x - 821,x2 - 10xy + 9y222,5xz - 5xy - x2 + 2xy - y223,(x2 + x + 1) ( x2 + x + 2) - 1224,(x+1) (x+2) (x+3) (x+4) - 2425,x3 + 2x2 - 2x - 12
Đọc tiếp
11,18y2 - 12xy + 2x2
12,(x2+x)2 + 3(x2+x) + 2
13,5x2 - 10xy + 5y2 - 20z2
14,x3 - 9x + 2x2 - 18
15,x2 - 2x - 4y2 - 4y
16,a2 + 2ab + b2 - 2a - 2b + 1
17,x3 - x + 3x2 y + 3xy2 + y3 - y
18,x3 + y3 + z3 - 3xyz
19,x2 + 4x - 5
20,2x2 - 6x - 8
21,x2 - 10xy + 9y2
22,5xz - 5xy - x2 + 2xy - y2
23,(x2 + x + 1) ( x2 + x + 2) - 12
24,(x+1) (x+2) (x+3) (x+4) - 24
25,x3 + 2x2 - 2x - 12
11: \(2x^2-12xy+18y^2\)
\(=2\left(x^2-6xy+9y^2\right)\)
\(=2\left(x-3y\right)^2\)
12: \(\left(x^2+x\right)^2+3\left(x^2+x\right)+2\)
\(=\left(x^2+x+2\right)\left(x^2+x+1\right)\)
Đúng 1
Bình luận (0)
Thực hiện nhanh các phép chia:a)
(
a
4
-
2
a
2
b
2
+
b
4
)
:
(
a
2
+
2
ab
+
b
2
)...
Đọc tiếp
Thực hiện nhanh các phép chia:
a) ( a 4 - 2 a 2 b 2 + b 4 ) : ( a 2 + 2 ab + b 2 ) ;
b) ( - 8 a 3 + 48 a 2 b - 96 ab 2 + 64 b 3 ) : (a - 2b).
a) Kết quả ( a – b ) 2 .
Gợi ý a 4 – 2 a 2 b 2 + b 4 = ( a 2 – b 2 ) 2 = ( a – b ) 2 ( a + b ) 2 .
b) Kết quả - 8 ( a – 2 b ) 2 .
Đúng 0
Bình luận (0)
Biết các số thực a,b thỏa mãn:
0
b
a
≤
2
và
2
a
b
≤
2
b
+
a
Tìm giá trị lớn nhất của F
a
2
+
b
2
Đọc tiếp
Biết các số thực a,b thỏa mãn: 0 < b < a ≤ 2 và 2 a b ≤ 2 b + a Tìm giá trị lớn nhất của F= a 2 + b 2
![]()
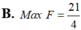
![]()
![]()





















