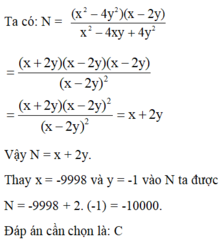64-x2+4xy-4y2

Những câu hỏi liên quan
Ai biết phần nào thì giải giúp mink nhé! cảm ơn!
Phân tích đa thức thành nhân tử:
a, x4 + 2x2 + 1 - x2
b,x4 + x2 + 1
c,y4 + 64
d,4xy +3z - 12y - xz
e,x2 - 4xy + 4y2 - z2 + 6z - 9
g, x2 - 4xy + 5x + 4y2 - 10y
h, x2 - 7x + 6
i, x3 + 5x2 + 6x + 2
a, \(x^4+2x^2+1-x^2\)
= \(\left(x^2+1\right)^2-x^2\)
= \(\left(x^2+x+1\right)\left(x^2-x+1\right)\)
b, \(x^4+x^2+1\)
= \(x^4+2x^2+1-x^2\)
= .. ( như phần a )
c, \(y^4+64\)
= \(\left(y^2+8\right)\left(y^2-8\right)\)
d, \(4xy+3z-12y-xz\)
\(=4y\left(x-3\right)-z\left(x-3\right)\)
\(=\left(x-3\right)\left(4y-z\right)\)
e, \(x^2-4xy+4y^2-z^2+6z-9\)
\(=\left(x-2y\right)^2-\left(z-3\right)^2\)
g, \(x^2-4xy+5x+4y^2-10y\)
\(=\left(x^2-4xy+4y^2\right)+\left(5x-10y\right)\)
\(=\left(x-2y\right)^2+5\left(x-2y\right)\)
\(=\left(x-2y\right)\left(x-2y+5\right)\)
h, \(x^2-7x+6\)
\(=x^2-6x-x+6\)
\(=x\left(x-6\right)-\left(x-6\right)\)
\(=\left(x-6\right)\left(x-1\right)\)
i, \(x^3+5x^2+6x+2\)
\(=x^3+x^2+4x^2+4x+2x+2\)
\(=x^2\left(x+1\right)+4x\left(x+1\right)+2\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+4x+2\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Biểu thức nào dưới đây là bình phương của hiệu x - 2y:
A. x2 + 2xy + 4y2.
B. x2 – 2xy + 4y2 .
C. x2 – 4xy + 4y2 .
D. x2 + 4xy + 4y2
Tính giá trị biểu thức N
(x
2
−
4y
2
)(x
−
2y)
x
2
−
4xy
+
4y
2
tại x -9998 và y -1. A. N -9996 B. N 10000 C. N -1...
Đọc tiếp
Tính giá trị biểu thức N = (x 2 − 4y 2 )(x − 2y) x 2 − 4xy + 4y 2 tại x = -9998 và y = -1.
A. N = -9996
B. N = 10000
C. N = -10000
D. N = -19997
x2+4xy-9+4y2
\(x^2+4xy-9+4y^2\)
\(=\left(x^2+4xy+4y^2\right)-9\)
\(=\left(x+2y\right)^2-3^2\)
\(=\left(x+2y+3\right)\left(x+2y-3\right)\)
Đúng 1
Bình luận (0)
\(=\left(x+2y\right)^2-9=\left(x+2y-3\right)\left(x+2y+3\right)\)
Đúng 0
Bình luận (0)
x2+4xy-4z2+4y2
= x^2+4xy+4y^2 -4z^2
= (x+2y)^2 -4z^2
=(x+2y-2z)(x+2y+2z)
Đúng 1
Bình luận (0)
\(=\left(x+2y-2z\right)\left(x+2y+2z\right)\)
Đúng 1
Bình luận (0)
=x2+4xy+4y2-4z2
=(x+2y)2-4z2
=(x+2y-4z)(x+2y+4z)
chắc chắn đúng
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
x2 + 4xy + 4y2 - 9
Đề bài yêu cầu gì thế em?
Đúng 0
Bình luận (0)
`x^2 +4xy+ 4y^2 -9`
`= (x^2 + 2x.2y + 4y^2) -9`
`= (x+2y)^2 - 3^2`
`= (x+2y -3)(x+2y +3)`
Đúng 2
Bình luận (0)
x2 + 4xy + 4y2 - 9
= (x2 + 4xy + 4y2)-32
= (x+2y)2 - 32
= (x+2y-3).(x+2y+3)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
x2 + 4y2 - 4xy - 4
\(x^2+4y^2-4xy-4\)
\(=\left(x^2-4xy+4y^2\right)-4\)
\(=\left(x-2y\right)^2-2^2\)
\(=\left(x-2y-2\right)\left(x-2y+2\right)\)
Đúng 2
Bình luận (0)
a, x2 + 4xy - 4z2 + 4y2 b,x2 + 2x - 15
\(x^2+4xy-4z^2+4y^2\)
\(=x^2+4xy+4y^2-4z^2\)
\(=\left(x+2y\right)^2-4z^2\)
\(=\left(x+2y-2z\right)\left(x+2y+2z\right)\)
\(x^2+2x-15\)
\(=x^2+2x+1-16\)
\(=\left(x+1\right)^2-16\)
\(=\left(x+1-4\right)\left(x+1+4\right)\)
\(=\left(x-3\right)\left(x+5\right)\)
Đúng 0
Bình luận (0)
a, 2x2 - 4xy + 2y2
b, x2 + 4xy + 4y2 - 9
c, x4 - x3y + x - y
\(2x^2-4xy+2y^2\\ =2\left(x^2-2xy+y^2\right)\\ =2\left(x-y\right)^2\)
Đúng 0
Bình luận (0)
a) 2x2-4xy+2y2
= 2x2-2xy-2xy+2y2
= 2x(x-y)-2y(x-y)
= (2x-2y)(x-y)
b) x2+4xy+4y2-9
= (x+2y)2-32
= (x+2y-3)(x+2y+3)
c) x4-x3y+x-y
= x3(x-y)+(x-y)
= (x3+1)(x-y)
Đúng 0
Bình luận (0)
\(a,=2\left(x^2-2xy+y^2\right)=2\left(x-y\right)^2\\ b,=\left(x+2y\right)^2-9=\left(x+2y-3\right)\left(x+2y+3\right)\\ c,=x^3\left(x-y\right)+\left(x-y\right)\\ =\left(x+1\right)\left(x-y\right)\left(x^2-x+1\right)\)
Đúng 0
Bình luận (0)
x2-y2-2x+2y
x2+4y2-25+4xy