Phân tích các đa thức sau thành nhân tử 

Những câu hỏi liên quan
Phân tích các đa thức sau thành nhân tử
d: \(9x^2-25=\left(3x-5\right)\left(3x+5\right)\)
e: \(16x^2-4y^2=4\left(4x^2-y^2\right)=4\left(2x-y\right)\left(2x+y\right)\)
f: \(\left(x+\dfrac{1}{4}\right)^2=x^2+\dfrac{1}{2}x+\dfrac{1}{16}\)
Đúng 2
Bình luận (0)
\(d,9x^2-25=\left(3x-5\right)\left(3x+5\right)\\ e,16x^2-4y^2=\left(4x-2y\right)\left(4x+2y\right)=4\left(2x-y\right)\left(2x+y\right)\)
Đúng 3
Bình luận (0)
d: \(9x^2-25=\left(3x-5\right)\left(3x+5\right)\)
e: \(16x^2-4y^2=4\left(4x^2-y^2\right)=4\left(2x-y\right)\left(2x+y\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Phân tích các đa thức sau thành nhân tử:
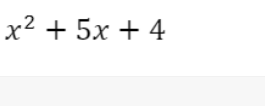
\(=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\)
Đúng 0
Bình luận (3)
Phân tích các đa thức sau thành nhân tử:
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
a: \(=-3xy\left(1-2x\right)\)
c: \(=\left(2x-y-5\right)\left(2x-y+5\right)\)
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tử
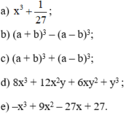
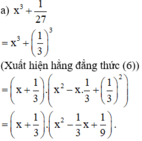
b) (a + b)3 – (a – b)3
(Xuất hiện hằng đẳng thức (7))
= [(a + b) – (a – b)][(a + b)2 + (a + b).(a – b) + (a – b)2]
= (a + b – a + b)(a2 + 2ab + b2 + a2 – b2+ a2 – 2ab + b2)
= 2b.(3a2+ b2)
c) (a + b)3 + (a – b)3
(Xuất hiện hằng đẳng thức (6))
= [(a + b) + (a – b)][(a + b)2 – (a + b)(a –b) + (a – b)2]
= [(a + b) + (a – b)][(a2 + 2ab + b2) – (a2 – b2) + (a2 – 2ab + b2)]
= (a + b + a – b)(a2 + 2ab + b2 – a2 + b2 + a2 – 2ab + b2)
= 2a.(a2 + 3b2)
d) 8x3 + 12x2y + 6xy2 + y3
= (2x)3 + 3.(2x)2.y + 3.2x.y2 + y3
(Xuất hiện hằng đẳng thức (4))
= (2x + y)3
e) –x3 + 9x2 – 27x + 27
= (–x)3 + 3.(–x)2.3 + 3.(–x).32 + 33
(Xuất hiện Hằng đẳng thức (4))
= (–x + 3)3
= (3 – x)3
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:
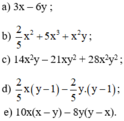
a) 3x – 6y
= 3.x – 3.2y
(Xuất hiện nhân tử chung là 3)
= 3(x – 2y)
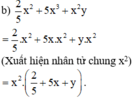
c) 14x2y – 21xy2 + 28x2y2
= 7xy.2x – 7xy.3y + 7xy.4xy
(Xuất hiện nhân tử chung 7xy)
= 7xy(2x – 3y + 4xy)
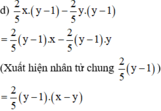
e) 10x(x – y) – 8y(y – x)
(Nhận thấy x – y = –(y – x) nên ta đổi y – x về x – y)
= 10x(x – y) – 8y[–(x – y)]
= 10x(x – y) + 8y(x – y)
= 2(x – y).5x + 2(x – y).4y
(Xuất hiện nhân tử chung 2(x – y))
= 2(x – y)(5x + 4y)
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:
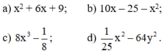
a) x2 + 6x + 9
= x2 + 2.x.3 + 32
(Xuất hiện hằng đẳng thức (1))
= (x + 3)2
b) 10x – 25 – x2
= –(–10x + 25 + x2)
= –(25 – 10x + x2)
= –(52 – 2.5.x + x2)
(Xuất hiện hằng đẳng thức (2) trong ngoặc)
= –(5 – x)2
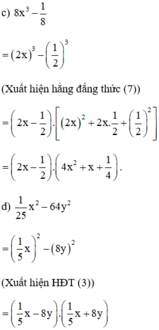
Đúng 0
Bình luận (0)
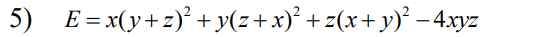 Phân tích các đa thức sau thành nhân tử
Phân tích các đa thức sau thành nhân tử
Lời giải:
$E=x(y^2+z^2+2yz)+y(z^2+x^2+2zx)+z(x^2+y^2+2xy)-4xyz$
$=x^2y+xy^2+yz^2+y^2z+z^2x+zx^2+2xyz$
$=xy(x+y)+yz(y+z)+zx(x+z)+2xyz$
$=xy(x+y+z)+yz(y+z+x)+zx(z+x)$
$=(x+y+z)(xy+yz)+zx(z+x)=(x+y+z).y(x+z)+xz(x+z)$
$=(x+z)[y(x+y+z)+xz]$
$=(x+z)[y(x+y)+(yz+xz)]$
$=(x+z)[y(x+y)+z(y+x)]=(x+z)(x+y)(y+z)$
Đúng 1
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:
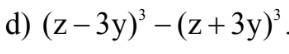
d: \(\left(z-3y\right)^3-\left(z+3y\right)^3\)
\(=\left[\left(z-3y\right)-\left(z+3y\right)\right]\left[\left(z-3y\right)^2+\left(z-3y\right)\left(z+3y\right)+\left(z+3y\right)^2\right]\)
\(=\left(z-3y-z-3y\right)\left(z^2-6zy+9y^2+z^2-9y^2+z^2+6zy+9y^2\right)\)
\(=\left(-6y\right)\cdot\left(3z^2+9y^2\right)\)
\(=-18y\cdot\left(z^2+3y^2\right)\)
Đúng 1
Bình luận (0)
Bài 1 : Phân tích các đa thức sau thành nhân tử :1) 15x + 15y 2) 8x - 12y3) xy - x 4) 4x^2- 6xBài 2 : Phân tích các đa thức sau thành nhân tử :1) 2(x + y) - 5a(x + y) 2) a^2(x - 5) - 3(x - 5)3) 4x(a - b) + 6xy(a - b) 4) 3x(x - 1) + 5(x -1)Bài 3 : Tính giá trị của biểu thức :1) A 13.87 + 13.12 + 132) B (x - 3).2x + (x - 3).y tại x 13 và y 4Bài 4 : Tìm x :1) x(x - 5) - 2(x - 5) 0 2) 3x(x - 4) - x + 4 03) x(x - 7) -...
Đọc tiếp
Bài 1 : Phân tích các đa thức sau thành nhân tử :
1) 15x + 15y 2) 8x - 12y
3) xy - x 4) 4x^2- 6x
Bài 2 : Phân tích các đa thức sau thành nhân tử :
1) 2(x + y) - 5a(x + y) 2) a^2(x - 5) - 3(x - 5)
3) 4x(a - b) + 6xy(a - b) 4) 3x(x - 1) + 5(x -1)
Bài 3 : Tính giá trị của biểu thức :
1) A = 13.87 + 13.12 + 13
2) B = (x - 3).2x + (x - 3).y tại x = 13 và y = 4
Bài 4 : Tìm x :
1) x(x - 5) - 2(x - 5) = 0 2) 3x(x - 4) - x + 4 = 0
3) x(x - 7) - 2(7 - x) = 0 4) 2x(2x + 3) - 2x - 3 = 0
\(1,\\ 1,=15\left(x+y\right)\\ 2,=4\left(2x-3y\right)\\ 3,=x\left(y-1\right)\\ 4,=2x\left(2x-3\right)\\ 2,\\ 1,=\left(x+y\right)\left(2-5a\right)\\ 2,=\left(x-5\right)\left(a^2-3\right)\\ 3,=\left(a-b\right)\left(4x+6xy\right)=2x\left(2+3y\right)\left(a-b\right)\\ 4,=\left(x-1\right)\left(3x+5\right)\\ 3,\\ A=13\left(87+12+1\right)=13\cdot100=1300\\ B=\left(x-3\right)\left(2x+y\right)=\left(13-3\right)\left(26+4\right)=10\cdot30=300\\ 4,\\ 1,\Rightarrow\left(x-5\right)\left(x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\\ 2,\Rightarrow\left(x-7\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ 3,\Rightarrow\left(3x-1\right)\left(x-4\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=4\end{matrix}\right.\\ 4,\Rightarrow\left(2x+3\right)\left(2x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Đúng 4
Bình luận (0)















