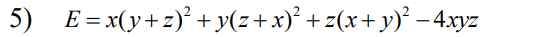Question

Phân tích các đa thức sau thành nhân tử 

Answer 1

Lời giải:
$E=x(y^2+z^2+2yz)+y(z^2+x^2+2zx)+z(x^2+y^2+2xy)-4xyz$

$=x^2y+xy^2+yz^2+y^2z+z^2x+zx^2+2xyz$

$=xy(x+y)+yz(y+z)+zx(x+z)+2xyz$

$=xy(x+y+z)+yz(y+z+x)+zx(z+x)$

$=(x+y+z)(xy+yz)+zx(z+x)=(x+y+z).y(x+z)+xz(x+z)$

$=(x+z)[y(x+y+z)+xz]$
$=(x+z)[y(x+y)+(yz+xz)]$

$=(x+z)[y(x+y)+z(y+x)]=(x+z)(x+y)(y+z)$