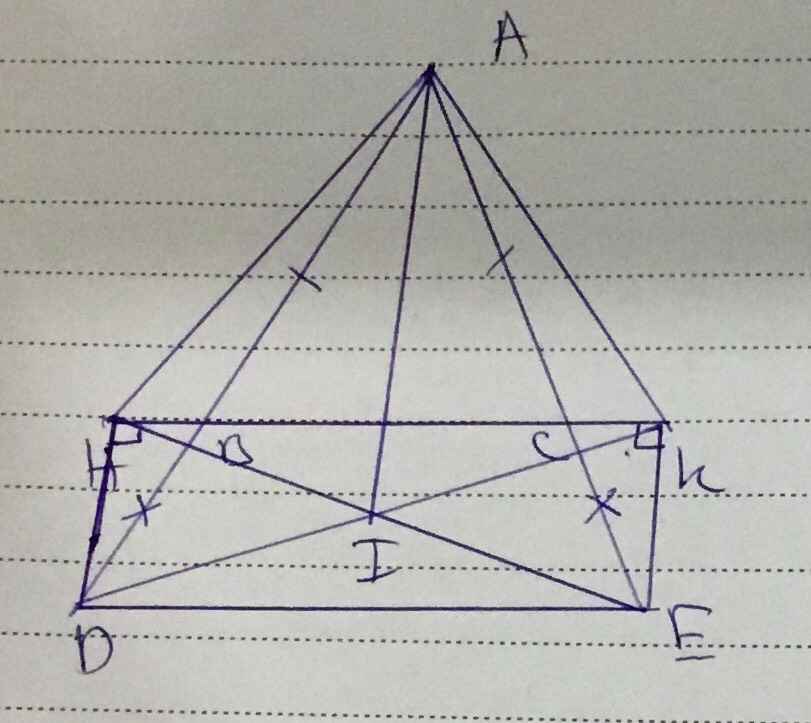
cho tam giác ABC nhọn vẽ phía ngoài tam giác ABC các đoạn thẳng BD=BA và CE=CA kẻ DH,EK vuông góc với đường thẳng BC chứng minh rằng DH+EK=BC

Những câu hỏi liên quan
Cho tam giác ABC có 3 góc nhọn . Vẽ về phía ngoài của tam giác ABC các đoạn thẳng BD BA BD BA = ⊥ , và CE CA CE CA = ⊥ , . Kẻ DH EK , vuông góc với đường thẳng BC (H và K thuộc đường thẳng BC). Chứng minh rằng : DH EK BC
Cho tam giác ABC có 3 góc nhọn . Vẽ về phía ngoài của tam giác ABC các đoạn thẳng BD=BA BD ⊥BA và CE=CA CE⊥ CA Kẻ DH EK , vuông góc với đường thẳng BC (H và K thuộc đường thẳng BC). Chứng minh rằng :DH+EK=BC
Từ A dựng đường thẳng vuông góc với BC căt BC tại M
Xét tg vuông ABM và tg vuông BDH có
\(BD\perp BA;HB\perp AM\Rightarrow\widehat{HBD}=\widehat{MAB}\) (góc có cạnh tương ứng vuông góc)
\(BD=BA\left(gt\right)\)
\(\Rightarrow\Delta BDH=\Delta ABM\) (hai tg vuông có cạnh huyền và 1 góc nhọn tương ứng bằng nhau)
\(\Rightarrow DH=BM\)
Chứng minh tương tự ta cũng có \(EK=CM\)
\(\Rightarrow DH+EK=BM+CM=BC\left(đpcm\right)\)
Cho tam giác ABC có ba góc nhọn. Vẽ về phía ngoài tam giác ABC các đoạn thẳng BD = BA, BD vuông góc với BA và CE = CA, CE vuông góc với CA. Kẻ DH, EK vuông góc với đường thẳng BC (K, H thuộc BC). Chứng minh DH + EK = BC
Kẻ đường cao AF.
Vì BD \(\perp\) BA nên \(\widehat{DBA}\) = 90o
Ta có: \(\widehat{DBH}\) + \(\widehat{DBA}\) + \(\widehat{ABF}\) = 180o
=> \(\widehat{DBH}\) + \(\widehat{ABF}\) = 90o (1)
Áp dụng tính chất tam giác vuông ta có:
\(\widehat{ABF}\) + \(\widehat{BAF}\) = 90o (2)
Từ (1) và (2) suy ra:
\(\widehat{DBH}\) + \(\widehat{ABF}\) = \(\widehat{ABF}\) + \(\widehat{BAF}\)
=> \(\widehat{DBH}\) = \(\widehat{BAF}\)
Xét \(\Delta\)BHD vuông tại H và \(\Delta\)AFB vuông tại F có:
BD = AB (gt)
\(\widehat{DBH}\) = \(\widehat{BAF}\) (c/m trên)
=> \(\Delta\)BHD = \(\Delta\)AFB (ch - gn)
=> DH = BF (2 cạnh t/ư) (3)
Chứng minh tương tự:
\(\Delta\)EKC = \(\Delta\)CFA (ch - gn)
=> EK = CF (2 cạnh t/ư) (4)
Ta có: BF + CF = BC (5)
Thay (3); (4) vào (5) ta được:
DH + EK = BC \(\rightarrow\) đpcm
Đúng 0
Bình luận (1)
Cho tam giác ABC có góc B và góc C nhọn, AB AC, đường cao AH. Vẽ đường thẳng BD BA, BD vuông góc với BA sao cho C và D khác phía đối với AB. Vẽ đoạn thẳng CE CA , CE vuông góc với CA sao cho B và E khác phía đối với AC. Kẻ DI vuông góc với BC tại I và EK vuông góc với BC tại K. Chứng minh : 1) góc ABH phụ với góc DBI 2) góc ABH góc BDI và góc BAH góc DBI 3) tam giác ABH tam giác DBI 4) tam giác ACH tam giác CEK 5) BI CK vẽ hình jum mx vs nha
Đọc tiếp
Cho tam giác ABC có góc B và góc C nhọn, AB < AC, đường cao AH. Vẽ đường thẳng BD = BA, BD vuông góc với BA sao cho C và D khác phía đối với AB. Vẽ đoạn thẳng CE = CA , CE vuông góc với CA sao cho B và E khác phía đối với AC. Kẻ DI vuông góc với BC tại I và EK vuông góc với BC tại K. Chứng minh : 1) góc ABH phụ với góc DBI 2) góc ABH = góc BDI và góc BAH = góc DBI 3) tam giác ABH = tam giác DBI 4) tam giác ACH = tam giác CEK 5) BI = CK vẽ hình jum mx vs nha
Cho tam giác ABC có góc B và góc C nhọn, AB AC, đường cao AH. Vẽ đường thẳng BD BA, BD vuông góc với BA sao cho C và D khác phía đối với AB. Vẽ đoạn thẳng CE CA , CE vuông góc với CA sao cho B và E khác phía đối với AC. Kẻ DI vuông góc với BC tại I và EK vuông góc với BC tại K. Chứng minh : 1) góc ABH phụ với góc DBI 2) góc ABH góc BDI và góc BAH góc DBI 3) tam giác ABH tam giác DBI 4) tam giác ACH tam giác CEK 5) BI CK vẽ hình jum mx vs nha
Đọc tiếp
Cho tam giác ABC có góc B và góc C nhọn, AB < AC, đường cao AH. Vẽ đường thẳng BD = BA, BD vuông góc với BA sao cho C và D khác phía đối với AB. Vẽ đoạn thẳng CE = CA , CE vuông góc với CA sao cho B và E khác phía đối với AC. Kẻ DI vuông góc với BC tại I và EK vuông góc với BC tại K. Chứng minh : 1) góc ABH phụ với góc DBI 2) góc ABH = góc BDI và góc BAH = góc DBI 3) tam giác ABH = tam giác DBI 4) tam giác ACH = tam giác CEK 5) BI = CK vẽ hình jum mx vs nha
Cho tam giác ABC có góc B và góc C nhọn, AB < AC, đường cao AH. Vẽ đường thẳng BD = BA, BD vuông góc với BA sao cho C và D khác phía đối với AB. Vẽ đoạn thẳng CE = CA , CE vuông góc với CA sao cho B và E khác phía đối với AC. Kẻ DI vuông góc với BC tại I và EK vuông góc với BC tại K. Chứng minh : 1) góc ABH phụ với góc DBI 2) góc ABH = góc BDI và góc BAH = góc DBI 3) tam giác ABH = tam giác DBI 4) tam giác ACH = tam giác CEK 5) BI = CK
trình bày bài này lâu lém
tự vận dụng kiến thức mà làm
suy nghĩ đi
động não đi
Đúng 0
Bình luận (0)
thế tớ hỏi làm gì bạn hay quá nhờ =)))
Đúng 0
Bình luận (0)
cho tam giác ABC (AB=AC) kẻ tia phân giác BD,CE
a) chứng minh BD=CE
b) kẻ DH vuông góc với BC , EK vuông góc với BC, chứng minh DH song song với EK, DH=EK
c BD cắt CE tại i chứng minh AI vuông góc với BC
a) Xét tam giác ABC ta có AB = AC
=> Tam giác ABC cân tại A
=> \(\widehat{ABC}\)= \(\widehat{ACB}\)
=> \(\frac{1}{2}\widehat{ABC}=\frac{1}{2}\widehat{ACB}\)
=> \(\widehat{ABD}=\widehat{DBC}=\widehat{ACE}=\widehat{ECB}\)
Xét tam giác ACE và tam giác ABD, ta có:
\(\widehat{A}\) chung
AC = AB (gt)
\(\widehat{ACE}=\widehat{ABD}\)
=> Tam giác ACE = tam giác ABD (g.c.g)
=> BD = CE
b) Ta có: \(\hept{\begin{cases}DH⊥BC\\EK⊥BC\end{cases}}\)
=> DH // EK
Xét tam giác DHB vuông tại H và
tam giác EKC vuông tại K, ta có:
BD = CE (cmt)
\(\widehat{DBH}\)(hay \(\widehat{DBC}\)) = \(\widehat{ECK}\)(hay \(\widehat{ECB}\)) (cmt)
=> Tam giác DHB = tam giác EKC (ch.gn)
=> DH = EK
Còn câu c mình không biết
Đúng 0
Bình luận (0)
a)Tam giác ABC có AB=AC suy ra tam giác ABC cân tại A suy ra góc B = C
Mà BD là tia phân giác của góc B ; CE là tia phân giác của góc C
suy ra góc ABD = CBD =BCE =ACE
Xét tam giác ABD và ACE có :
góc ABD =góc ACE (cmt )
AB = AC (gt)
Chung gócA
suy ra tam giác ABD = ACE (g.c.g )
suy ra BD = CE ( 2 cạnh tương ứng )
b) Ta có DH vuông góc với BC ; EK vuông góc với BC
suy ra DH song song với EK
Xét tam giác CEK và BDH có :
BD= CE ( cm ở ý a)
góc CKE = góc BHD ( = 90 độ )
góc CBD = BCE ( cm ở ý a )
suy ra tam giác CEK= BDH (ch-gn)
suy ra DH = EK ( 2 cạnh tương ứng )
c) Xét tam giác BIC có góc CBD =BCE ( cm ở ý a ) suy ra tam giác BIC cân tại I
suy ra BI = CI ( t/c tam giác cân )
Xét tam giác AIC và AIB có :
AB =AC ( gt )
góc ACE = ABD ( cm ở ý a )
CI = BI ( cmt)
suy ra tam giác AIC = AIB ( c.g.c)
suy ra góc IAC = IAB (2 góc tương ứng )
suy ra AI là tia phân giác của góc BAC (1)
Mà tam giác ABC cân tại A ( 2)
Từ ( 1 ) và ( 2 ) suy ra AI vuông góc với BC
( nếu đúng nhớ kết bạn với tớ nhé ^-^)
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a trên tia đối của tia ba lấy điểm d trên tia đối của tia ca lấy điểm e sao cho bd=ce vẽ dh và ek cùng vuông góc với đường thẳng bc chứng minh
Hình vẽ đây em nhé. Sửa lại câu hỏi không có nói chứng minh gì nên a không giải được đâu nhé
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A,kẻ phân giác BD của góc B,kẻ phân giác CE của góc C
1) Chứng minh BD=CE
2) Kẻ Dh vuông góc với BC,EK vuông góc với BC.Chứng minh
a)DH//EK
b)DH=EK
1) Ta có: \(\widehat{ABD}=\widehat{CBD}=\dfrac{\widehat{ABC}}{2}\)(BD là tia phân giác của \(\widehat{ABC}\))
\(\widehat{ACE}=\widehat{BCE}=\dfrac{\widehat{ACB}}{2}\)(CE là tia phân giác của \(\widehat{ACB}\))
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{CBD}=\widehat{ACE}=\widehat{BCE}\)
Xét ΔABD và ΔACE có
\(\widehat{BAD}\) chung
AB=AC(ΔABC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
Do đó: ΔABD=ΔACE(g-c-g)
Suy ra: BD=CE(hai cạnh tương ứng)
2) Ta có: EK⊥BC(gt)
DH⊥BC(gt)
Do đó: EK//DH(Định lí 1 từ vuông góc tới song song)
Ta có: ΔABD=ΔACE(cmt)
nên AD=AE(hai cạnh tương ứng)
Ta có: AE+EB=AB(E nằm giữa A và B)
AD+DC=AC(D nằm giữa A và C)
mà AB=AC(ΔABC cân tại A)
và AE=AD(cmt)
nên EB=DC
Xét ΔEKB vuông tại K và ΔDHC vuông tại H có
EB=DC(cmt)
\(\widehat{EBK}=\widehat{DCH}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔEKB=ΔDHC(cạnh huyền-góc nhọn)
Suy ra: EK=DH(hai cạnh tương ứng)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A lấy D trên AB, lấy E trên AC sao cho BD=CE . Kẻ các đường vuông góc DH vuông góc BC . EK vuông góc BC a) Chứng mình DH song song EK b) Chứng minh tam giác BDH=CEK
a: DH vuông góc BC
EK vuông góc BC
=>DH//EK
b: góc BDH+góc B=90 độ
góc CEK+góc C=90 độ
góc B=góc C
=>góc BDH=góc CEK
Đúng 0
Bình luận (0)


















