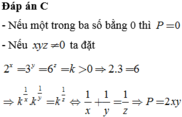Tìm các số x , y, z thỏa mãn đồng thời 2x=3y=4z và xy+yz+zx = 6

Những câu hỏi liên quan
cho các số thực x,y,z thỏa mãn 2x+3y-z=4. Tìm min max của A =xy+yz+zx
Cho x, y, z là các số thực thỏa mãn 2 x = 3 y = 6 z . Rút gọn P = x y + y z + z x .
A. P=0
B.P=xy
C. P=2xy
D. p=3xy
Đáp án C
- Nếu một trong ba số bằng 0 thì P=0
- Nếu x y z ≠ 0 ta đặt
2 x = 3 y = 6 z = k > 0 ⇒ 2.3 = 6
⇒ k 1 x . k 1 y = k 1 z ⇔ 1 x + 1 y = 1 z ⇒ P = 2 x y
Đúng 0
Bình luận (0)
Cho x, y, z là các số thực thỏa mãn 2 x = 3 y = 6 z . Rút gọn P = x y + y z + z x
A. 0
B. xy
C. 2xy
D. 3xy
Tìm các số nguyên dương x;y;z thỏa mãn: xy(x+y)=6;yz(y+z)=12;zx(z+x)=30
Tìm x, y, z thỏa mãn:
xy/2y+4x=yz/4z+6y=zx/6x+2x=xyz/x+y+z (x,y,z khác 0)
Nếu biết cách thì làm theo cách lớp 7 thui nhé!
Cho x,y,z là các số thỏa mãn điều kiện xy+2(yz+zx)=5. Tìm GTNN của biểu thức S=3(x2+y2)+4z2
Bài này có nhiều cách, xin phép làm 2 cách đơn giản. Tuy nhiên ở cách 2 tính sai chỗ nào thì tự check:) (chắc ko sai đâu:v đừng lo quá mức)
Cách 1: \(x^2+y^2\ge2xy\)
\(2x^2+2z^2\ge4xz\)
\(2y^2+2z^2\ge4yz\)
Cộng theo vế 3 bđt trên kết hợp giả thiết suy ra \(S\ge10\)
Cách 2:
Xét \(S-2\left[xy+2yz+2zx\right]\)
\(=\left(x-y\right)^2+2\left(y-z\right)^2+2\left(z-x\right)^2\ge0\)
Do đó...
Đúng 0
Bình luận (0)
Tuy nhiên, sau đây mới là cách phân tích ngắn nhất chỉ với 2 bình phương không âm!
Ta có:\(S-2\left[xy+2\left(yz+zx\right)\right]\)\(=2\left(x-y\right)^2+\left(x+y-2z\right)^2\ge0\)
Vậy \(S\ge10\). It's verry beautiful!
Cho các số thực x, y, z thỏa mãn đồng thời các điều kiện sau x + y + z = 2, x^2 + y^2 z^2 = 18 và xyz = -1. Tính giá trị của S = 1/(xy + z - 1) + 1/(yz + x -1) + 1/(zx + y -1)
Cho x,y,z là các số thực dương thỏa mãn đẳng thức xy+yz+zx=5. Tìm giá trị nhỏ nhất của biểu thức
\(P=\frac{3x+3y+3z}{\sqrt{6\left(x^2+5\right)}+\sqrt{6\left(y^2+5\right)}+\sqrt{6\left(z^2+5\right)}}\)
Mình nghĩ phần phân thức là $3x+3y+2z$ thay vì $3x+3y+3z$. Nếu là vậy thì bạn tham khảo lời giải tại link sau:
Cho x, y, z là các số thực dương thỏa mãn đẳng thức xy yz zx=5. Tìm GTNN của biểu thức \(P=\frac{3x 3y 2z}{\sqrt{6\left(... - Hoc24
Đúng 1
Bình luận (2)
Tìm số thực z,y,z thoả mãn
xy / 2y+4x = yz / 4z+6x = zx/ 6x+2z = x^2+y^2+z^2 / 2^2+4^2+6^2