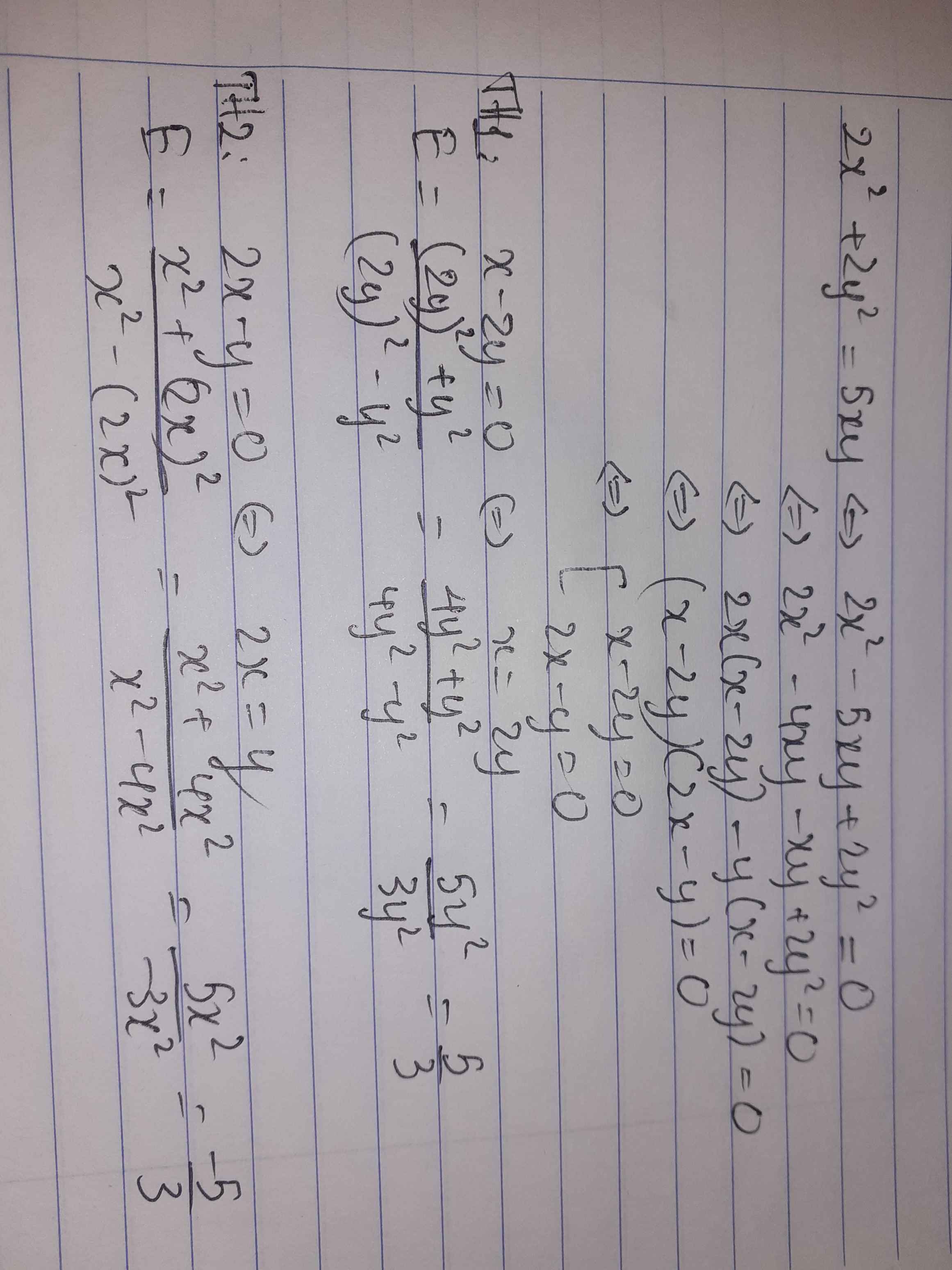Cho x>y>0 và 2x2+2y2=5xy. Tính : \(E=\frac{x+y}{x-y}\).

Những câu hỏi liên quan
Cho 2x2+2y2=5xy và 0<x<y .Tính giá trị cưa E =x+y/x-y
2x2 + 2y2 = 5xy
=> 2x2 + 2y2 - 5xy = 0
=> (x - 2y)(2x - y) = 0
x = 2y (loại)
y = 2x
E = \(\dfrac{x+2x}{x-2x}\)=-3
Đúng 2
Bình luận (0)
1, Phân tích đa thức thành nhân tử:
a,f(x;y)=2x2+5xy+2y2-5x-4y+2
b, Cho x + y = 5.Tính GTBT: N=x3+y3–2x2–2y2+3xy(x+y)–4xy+3(x+y)+10
\(x^3+y^3-2x^2-2y^2+3xy\left(x+y\right)-4xy+3\left(x+y\right)+10=\left[x^3+y^3+3xy\left(x+y\right)\right]-2\left(x^2+2xy+y^2\right)+3\left(x+y\right)+10=\left(x+y\right)^3-2\left(x+y\right)^2+3\left(x+y\right)+10=5^3-2.5^2+3.5+10=100\)
Đúng 0
Bình luận (0)
Cho \(2x^2+2y^2=5xy\)và 0<x<y
Tính giá trị của \(E=\frac{x+y}{x-y}\)
ta có\(2x^2+2y^2=5xy\)
\(\Leftrightarrow2x^2-5xy+2y^2=0\)\(\Leftrightarrow\left(x-4y\right)\left(2x-y\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=4y\\2x=y\end{cases}}\)
Vì\(0< x< y\)\(\Rightarrow x=4y\)là vô lý
\(\Rightarrow2x=y^{\left(1\right)}\)
Thế (1)vào biểu thức E ta được:
\(E=\frac{x+y}{x-y}=\frac{x+2x}{x-2x}=\frac{3x}{-x}=-3\)
Vậy biểu thức E có giá trị là 3
Xong rồi đấy nhớ k cho mình nhé!
Đúng 0
Bình luận (0)
Cho \(0< x< y\) và \(2x^2+2y^2=5xy\)
Tính \(E=\dfrac{x^2+y^2}{x^2-y^2}\)
cho các số dương x,y,z thỏa mãn x+y+z=1 tìm min của biểu thức
P=√(2x2+xy+2y2) +√(2y2+yz+2z2)+ √(2z2+xz+2x2)
Ta có: \(2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x^2+2xy+y^2\right)=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\)
Theo BĐT Bunhacopxky: \(\left(x^2+y^2\right)\left(1+1\right)\ge\left(x+y\right)^2\Rightarrow\dfrac{3}{2}\left(x^2+y^2\right)\ge\dfrac{3}{4}\left(x+y\right)^2\\ \Rightarrow2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\ge\dfrac{5}{4}\left(x+y\right)^2\\ \Rightarrow\sqrt{2x^2+xy+2y^2}\ge\dfrac{\sqrt{5}}{2}\left(x+y\right)\)
Chứng minh tương tự:
\(\sqrt{2y^2+yz+2z^2}\ge\dfrac{\sqrt{5}}{2}\left(y+z\right)\\ \sqrt{2z^2+xz+2x^2}\ge\dfrac{\sqrt{5}}{2}\left(x+z\right)\)
Cộng vế theo vế, ta được: \(P\ge\sqrt{5}\left(x+y+z\right)=\sqrt{5}\cdot1=\sqrt{5}\)
Dấu "=" \(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
Đúng 2
Bình luận (0)
Bạn tham khảo nhé
https://hoc24.vn/cau-hoi/cho-cac-so-duong-xyz-thoa-man-xyz1cmrcan2x2xy2y2can2y2yz2z2can2z2zx2x2can5.182722154737
Đúng 1
Bình luận (0)
Cho 2x2+2y2=5xy và 0<x<y. Tính E = x+y/x-y
Cho 2x2+2y2=5xy và 0<x<y. Tính E = x+y/x-y
Giải:
Cho 2x2+2y2=5xy và 0<x<y. => \(\frac{x}{y}< 1\)
Chia cả hai vế cho y^2 ta có: \(2\left(\frac{x}{y}\right)^2-5\frac{x}{y}+2=0\) (1)
Đặt: t = x/y ta có: 0 < t < 1
(1) trở thành: \(2t^2-5t+2=0\)
<=> \(\left(2t^2-4t\right)+\left(-t+2\right)=0\)
<=> \(2t\left(t-2\right)-\left(t-2\right)=0\)
<=> \(\left(2t-1\right)\left(t-2\right)=0\)
<=> t = 1/2 ( tm)
Hoặc t = 2 loại
Với t = 1/2 ta có: x/y = 1/2
<=> y = 2x
\(E=\frac{x+y}{x-y}=\frac{x+2x}{x-2x}=\frac{3x}{-x}=-3\)
Cho : \(2x^2+2y^2=5xy\) .Tính \(E=\frac{x+y}{x-y}\left(0< x< y\right)\)
GT=>(2x-y)(x-2y)=0
Do 0<x<y nên x-2y<0
Do đó 2x-y=0 hay 2x=y
Thay y=2x vào E đượcE=-3
Đúng 0
Bình luận (0)
Ta có: \(2\left(x^2+y^2\right)=5xy\)
\(x^2+y^2=\frac{5}{2}xy\)
\(E^2=\left(\frac{x+y}{x-y}\right)^2=\frac{\left(x+y\right)^2}{\left(x-y\right)^2}=\frac{x^2+2xy+y^2}{x^2-2xy+y^2}\)
Hay: \(\frac{\frac{5}{2}xy+2xy}{\frac{5}{2}xy+2xy}=\frac{4,5xy}{0,5xy}=9\)
\(\Rightarrow E=\sqrt{9}=\pm3\)
vì 0<x<y
=>E=3
Đúng 0
Bình luận (0)
Ta có:\(2x^2+2y^2=5xy\Leftrightarrow2x^2+2y^2+4xy=9xy\Leftrightarrow2\left(x+y\right)^2=9xy\Leftrightarrow\left(x+y\right)^2=\frac{9xy}{2}\) (1)
Mặt khác \(2x^2+2y^2=5xy\Leftrightarrow2x^2+2y^2-4xy=xy\Leftrightarrow2\left(x-y\right)^2=xy\Leftrightarrow\left(x-y\right)^2=\frac{xy}{2}\) (2)
Từ (1) và (2) => \(\frac{\left(x+y\right)^2}{\left(x-y\right)^2}=\frac{\frac{9xy}{2}}{\frac{xy}{2}}\Leftrightarrow\left(\frac{x+y}{x-y}\right)^2=9\Leftrightarrow\frac{x+y}{x-y}=\pm3\)
Mà \(0< x< y\Rightarrow E=\frac{x+y}{x-y}=-3\)
Vậy E=-3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho x, y ,z là các số thực không âm thoả mãn x + y + z = 1. Tính giá trị biểu thức P= √2x2+x+1 + √2y2+y+1 + √2z2+z+1
Biểu thức này không có giá trị cụ thể. Bạn xem lại đề.
Đúng 0
Bình luận (0)