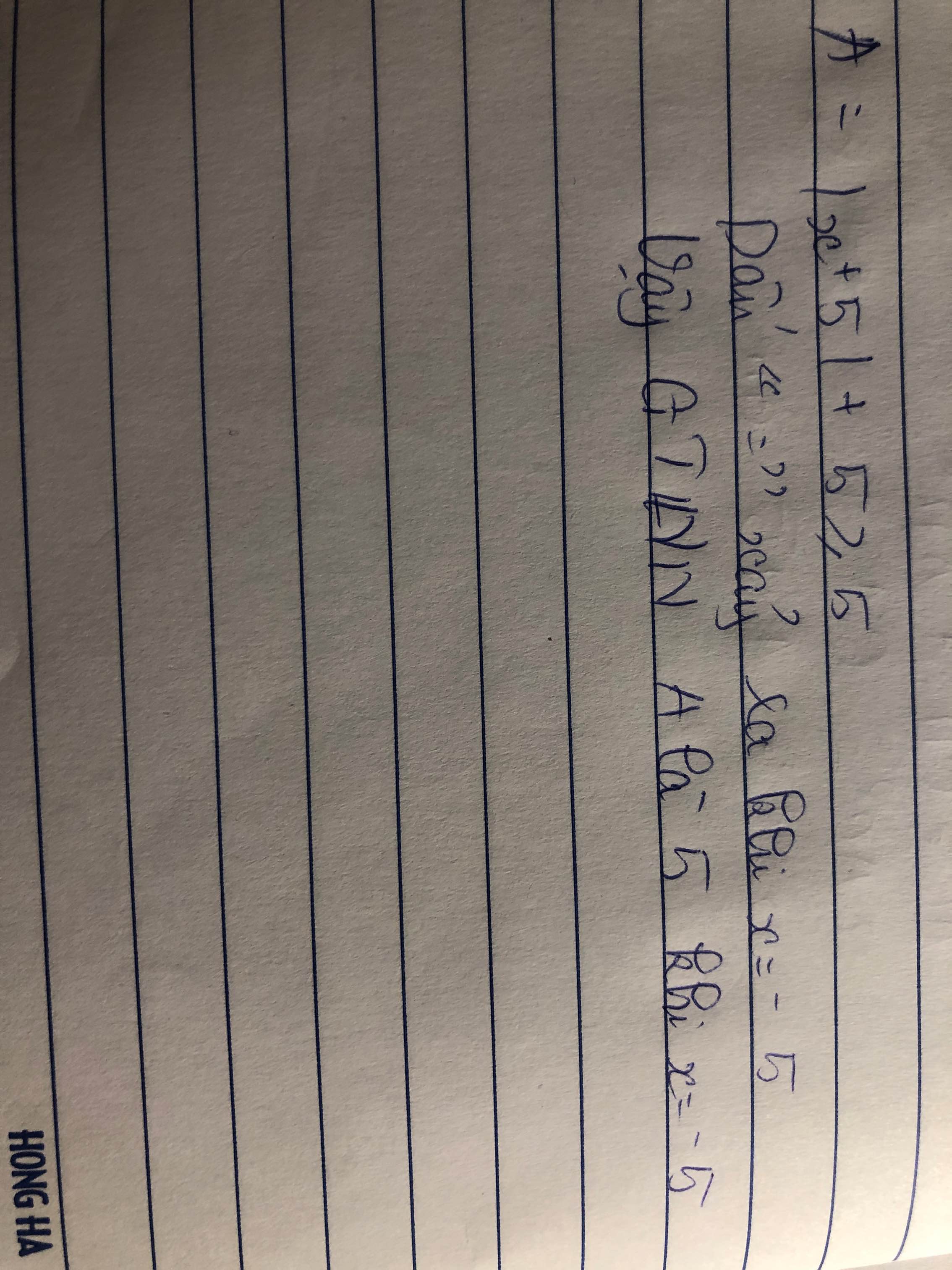Tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức sau: B=|6-2x|-5

Những câu hỏi liên quan
Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức sau:
a) S= 3/2x²+2x+3
b) T= 5/3x²+4x+15
c) V= 1/-x²+2x-2
d) X= 2/-4x²+8x+5
c: \(-x^2+2x-2=-\left(x-1\right)^2-1\le-1\forall x\)
\(\Leftrightarrow V\ge-1\forall x\)
Dấu '=' xảy ra khi x=1
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức
A=10-|x|-(y+4)4
B=|2x+6|+(x-y)2-5
tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức sau
B=|6-2X|-5
C=3-|X+1|
D=-100-|7-X|
E=5-|2X+6|-|7-Y|
GIÚP MK NHA MK TC CHO NHÌU
Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức sau:
a) S= \(\dfrac{3}{2x^2+2x+3}\)
b) T= \(\dfrac{5}{3x^2+4x+15}\)
c) V= \(\dfrac{1}{-x^2+2x-2}\)
d) X= \(\dfrac{2}{-4x^2+8x-5}\)
a. Tìm giá trị lớn nhất của biểu thức: B = 10\(-5-\left(2x-5\right)^2\)
b. Tìm giá trị nhỏ nhất của biểu thức :C = |2x -4|- |2x- 6|
a. ta có (2x-5)2 >= 0 với mọi x thuộc R
vậy 5 -(2x-5)2 <= 5
dấu = xảy ra khi (2x-5)2=0
vậy 2x-5=0
2x =5
x= 5/2=2,5
Vậy để B lớn nhất thì x=2,5
b. ta có | 2x-4| >= 0 với mọi x thuộc R
| 2x-6| >= 0 với mọi x thuộc R
vậy | 2x-4 |- |2x-6| >= 0
dấu = xảy ra khi |2x-4| và |2x-6| đều bằng 0
=> 2x-4=0 => 2x - 6=0
2x =4 2x =6
x=4/2=2 x= 6/2=3
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức sau :
A =l x + 5 l + 5
Với mọi x ta có :
\(\left|x+5\right|\ge0\)
\(\Leftrightarrow\left|x+5\right|+5\ge0\)
\(\Leftrightarrow A\ge5\)
Dấu "=" xảy ra \(\Leftrightarrow x=-5\)
Vậy..
Đúng 3
Bình luận (1)
Với mọi giá trị của x, ta có:
|x+5|≥0
⇔|x+5|+5≥0
⇔|x+5|+5≥5
Hay A≥5 Với mọi giá trị của x
Để A=5 thì:
|x+5|+5=5
⇔|x+5| =0
⇔x+5 =0
⇔x =\(-5\)
Vậy Amax=5⇔x=-5
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của biểu thức:
a) D= 5-( 2x- 1)4
Ta có :
\(\left(2x-1\right)^4\ge0\forall x\)
\(\Rightarrow5-\left(2x-1\right)^4\le5\forall x\)
Dấu " = " xảy ra
\(\Leftrightarrow\left(2x-1\right)^4=0\)
\(\Leftrightarrow2x-1=0\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\frac{1}{2}\)
Vậy \(GTLN\)của D là 5 \(\Leftrightarrow x=\frac{1}{2}\)
Tham khảo nha !!!
Đúng 0
Bình luận (0)
Có :D=(2x-1)^4 > hoặc = 0
=> 5-(2x-1)^4< hoặc = 5
Dấu = xảy ra <=>(2x-1)^4 = 0
=>2x-1 = 0
2x=1
x=1/2
Vậy gtln của D=5 khi và chỉ khi x=1/2
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của biểu thức sau
a,(2x-3)^4-2
b,(x^2-9)^2+/y-3/-1
c,-/x+5/+2
d,2-x^2
Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của các biểu thức sau:
Đọc tiếp
Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của các biểu thức sau:
\(A=\left(x-4\right)^2+1\)
Ta có: \(\left(x-4\right)^2\ge0\Rightarrow\left(x-4\right)^2+1\ge1\Rightarrow A\ge1\)
\(A_{min}=1\Leftrightarrow x=4\)
\(B=\left|3x-2\right|-5\)
Ta có: \(\left|3x-2\right|\ge0\Rightarrow\left|3x-2\right|-5\ge-5\Rightarrow B\ge-5\)
\(B_{min}=-5\Leftrightarrow x=\dfrac{2}{3}\)
\(C=5-\left(2x-1\right)^4\)
Ta có: \(\left(2x-1\right)^4\ge0\forall x\Rightarrow-\left(2x-1\right)^4\le0\forall x\Rightarrow5-\left(2x-1\right)^4\le5\Rightarrow C\le5\)
\(C_{max}=5\Leftrightarrow x=\dfrac{1}{2}\)
\(D=-3\left(x-3\right)^2-\left(y-1\right)^2-2021\)
Ta có: \(\left\{{}\begin{matrix}-3\left(x-3\right)^2\le0\forall x\\-\left(y-1\right)^2\le0\forall y\end{matrix}\right.\Rightarrow-3\left(x-3\right)^2-\left(y-1\right)^2\le0\forall x,y\Rightarrow-3\left(x-3\right)^2-\left(y-1\right)^2-2021\le-2021\Rightarrow D\le-2021\)
\(D_{max}=-2021\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
\(E=-\left|x^2-1\right|-\left(x-1\right)^2-y^2-2020\)
\(=-\left|\left(x-1\right)\left(x+1\right)\right|-\left(x-1\right)^2-y^2-2020\)
Ta có: \(\left\{{}\begin{matrix}\left|\left(x-1\right)\left(x+1\right)\right|\ge0\forall x\Rightarrow-\left|\left(x-1\right)\left(x+1\right)\right|\le0\\\left(x-1\right)^2\ge0\forall x\Rightarrow-\left(x-1\right)^2\le0\\y^2\ge0\Rightarrow-y^2\le0\end{matrix}\right.\Rightarrow E\le-2020\)
\(E_{max}=-2020\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)