Trong mặt phẳng tọa độ cho hai điểm A(0;-1) và B(1;2)
a) Viết phương trình đường thẳng đi qua A và B.
b) Điểm C (-1;-4) có nằm trên đường thẳng đó không?
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy cho hai điểm A(1,0) và B(0,-2). Tọa độ trung điểm của đoạn thẳng AB là
Gọi M là trung điểm AB
\(\Rightarrow\left\{{}\begin{matrix}x_M=\frac{x_A+x_B}{2}=\frac{1+0}{2}=\frac{1}{2}\\y_M=\frac{y_A+y_B}{2}=\frac{0-2}{2}=-1\end{matrix}\right.\)
\(\Rightarrow M\left(\frac{1}{2};-1\right)\)
Đúng 0
Bình luận (0)
Gọi I là TĐ AB
\(\Rightarrow\left\{{}\begin{matrix}x_I=\frac{x_A+x_B}{2}\\y_I=\frac{y_A+y_B}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_I=\frac{1+0}{2}\\y_I=\frac{0-2}{2}\end{matrix}\right.\Rightarrow I\left(\frac{1}{2};-1\right)\)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;1;1) và hai mặt phẳng (P):2x-y+3z-10, (Q): y0. Viết phương trình mặt phẳng chứa A, vuông góc với cả hai mặt phẳng và ? A. 3x+y-2z-20 B. 3x-2z0 C. 3x-2z-10 D. 3x-y+2z-40
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;1;1) và hai mặt phẳng (P):2x-y+3z-1=0, (Q): y=0. Viết phương trình mặt phẳng chứa A, vuông góc với cả hai mặt phẳng và ?
A. 3x+y-2z-2=0
B. 3x-2z=0
C. 3x-2z-1=0
D. 3x-y+2z-4=0
Đáp án C
Phương pháp
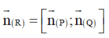
Cách giải: Ta có:
là 1 VTPT của mặt phẳng (R).
Vậy phương trình mặt phẳng (R):
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
−
1
;
2
;
3
và hai mặt phẳng
P
:
x
−
2
0
và
Q
:
y
−
z
−
1
0
. Viết phương trình mặt phẳng đi qua A và vuông góc với hai mặt phẳng ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A − 1 ; 2 ; 3 và hai mặt phẳng P : x − 2 = 0 và Q : y − z − 1 = 0 . Viết phương trình mặt phẳng đi qua A và vuông góc với hai mặt phẳng P , Q
A. x + y + z − 5 = 0
B. x + z = 0
C. y + z − 5 = 0
D. x + y + 5 = 0
Đáp án C
Ta có n P → 1 ; 0 ; 0 ; n Q → 0 ; 1 ; − 1 suy ra n → = n P → ; n Q → = 0 ; 1 ; 1
Suy ra phương trình mặt phẳng cần tìm là: y + z − 5 = 0
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A và B phân biệt. Biết AB song song với mặt phẳng (zOx) và không song song với hai mặt phẳng (xOy), (yOz). Tọa độ của
A
B
⇀
có thể là (với a,b#0) A. (0;a;b) B. (a;b;0) C. (a;0;0) D. (a;0;b).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A và B phân biệt. Biết AB song song với mặt phẳng (zOx) và không song song với hai mặt phẳng (xOy), (yOz). Tọa độ của A B ⇀ có thể là (với a,b#0)
A. (0;a;b)
B. (a;b;0)
C. (a;0;0)
D. (a;0;b).
Trong không gian tọa độ Oxyz cho điểm
A
1
;
2
;
3
và hai mặt phẳng
P
:
x
−
y
0
,
Q
:
2
x
+
4
z
+
1
0
. Phương trình mặt phẳng (R) đi qua A và chứa giao tuyến của hai mặt phẳng (P),(Q) là A....
Đọc tiếp
Trong không gian tọa độ Oxyz cho điểm A 1 ; 2 ; 3 và hai mặt phẳng P : x − y = 0 , Q : 2 x + 4 z + 1 = 0 . Phương trình mặt phẳng (R) đi qua A và chứa giao tuyến của hai mặt phẳng (P),(Q) là
A. R : − 2 x + 2 y − z + 3 = 0.
B. R : 2 x − 2 y − z + 3 = 0.
C. R : 2 x + 2 y + 3 z − 17 = 0.
D. R : x - y + 1 = 0.
Đáp án D
Gọi d = P ∩ Q ,d có VTCP là u → .
Khi đó u → = 1 ; − 1 ; 0 , 2 ; 0 ; 4 = − 4 ; − 4 ; 2 = − 2 2 ; 2 ; − 1 .
Mặt phẳng (R) qua A 1 ; 2 ; 3 , có VTCP là 2 ; 2 ; − 1 và đi qua điểm B ( − 1 2 ; − 1 2 ; 0 ) thuộc giao tuyến, (R) có phương trình là R : x − y + 1 = 0.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;4;1), B(-1;1;3) và mặt phẳng (P):x - 3y + 2z - 5 0. Viết phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P). A.
Q
:
2
y
+
3
z
-
1
0
B.
Q
:
2
x
+
3
z
-
12
0
C.
Q
:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;4;1), B(-1;1;3) và mặt phẳng (P):x - 3y + 2z - 5 = 0. Viết phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P).
A. Q : 2 y + 3 z - 1 = 0
B. Q : 2 x + 3 z - 12 = 0
C. Q : 2 x + 3 z - 11 = 0
D. Q : 2 y + 3 z - 11 = 0
Đáp án D
Ta có B A → = 3 ; 3 ; - 2 và (P) có véc tơ pháp tuyến n → = 1 ; - 3 ; 2 .
Gọi n ' → là véc tơ pháp tuyến của mặt phẳng (Q), để (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) thì: n → ⊥ n ' → ⊥ B A → ⇒ n ' = n → , B A → = 0 ; - 8 ; - 12 ⇒ Q : 0 x - 2 - 8 y - 4 - 12 z - 1 = 0 ⇔ 2 y + 3 z - 11 = 0
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;0;1), B(2;1;2) và mặt phẳng (P):x+2y+3z+30. Phương trình mặt phẳng
(
α
)
đi qua hai điểm A, B và vuông góc với mặt phẳng là: A. x + 2y -z +6 0 B.x + 2y -3z +6 0 C. x -2y + z-2 0 D. x + 2y -3z +6 0
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;0;1), B(2;1;2) và mặt phẳng (P):x+2y+3z+3=0. Phương trình mặt phẳng ( α ) đi qua hai điểm A, B và vuông góc với mặt phẳng là:
A. x + 2y -z +6 =0
B.x + 2y -3z +6 =0
C. x -2y + z-2 =0
D. x + 2y -3z +6 =0
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A
1
;
0
;
1
;
B
2
;
1
;
2
và mặt phẳng
P
:
x
+
2
y
+
3
z
+
3
0
. Phương trình mặt...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 1 ; 0 ; 1 ; B 2 ; 1 ; 2 và mặt phẳng P : x + 2 y + 3 z + 3 = 0 . Phương trình mặt phẳng α đi qua hai điểm A, B và vuông góc với mặt phẳng (P) là:
A. x + 2y - z + 6 = 0
B. x + 2y - 3z + 6 = 0
C. x - 2y + z - 2 = 0
D. x + 2y - 3z + 6 = 0
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1; 0; 0), B (0; 0; 2) và mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
2
y
+
1
0
Số mặt phẳng chứa hai điểm A, B và tiếp xúc với mặt cầu (S) là: A. mặt phẳng. B. mặt phẳng C. mặt phẳng D. Vô số mặt phẳng.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1; 0; 0), B (0; 0; 2) và mặt cầu S : x 2 + y 2 + z 2 - 2 x - 2 y + 1 = 0 Số mặt phẳng chứa hai điểm A, B và tiếp xúc với mặt cầu (S) là:
A. mặt phẳng.
B. mặt phẳng
C. mặt phẳng
D. Vô số mặt phẳng.
Chọn A
Gọi phương trình mặt phẳng là
Theo đề bài, mặt phẳng qua A, B nên ta có:
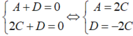
Vậy mặt phẳng (P) có dạng: 2Cx + 2By + Cz - 2C = 0. (S) có tâm I (1; 1; 0) và R = 1
Vì (P) tiếp xúc với (S) nên d(I, (P)) = R
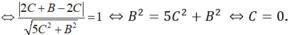
Suy ra A = D = 0. Vậy phương trình mặt phẳng (P): y = 0
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (-1; -2; 0), B (0; -4; 0), C (0; 0; -3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
A
.
P
:
2
x
-
y
+
3
z
0
B
.
P
:
6
x
-
3
y
+
5
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (-1; -2; 0), B (0; -4; 0), C (0; 0; -3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
A . P : 2 x - y + 3 z = 0
B . P : 6 x - 3 y + 5 z = 0
C . P : 2 x - y - 3 z = 0
D . P : - 6 x + 3 y + 4 z = 0
