trong mặt phẳng toạ độ oxy
a)vẽ tam giác abc,biết A(2;4);B(2;-1);C(-4:-1)
b)tam giác abc là tam giác gì?tính diện tích của tam giác.
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy
a) Vẽ tam giác ABC, biết A(2;4) ; B(2;-1) ; C(-4;-1)
b) Tam giác ABC là tam giác gì ? Tính diện tích của tam giác đó.
b) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(2-2\right)^2+\left(4+1\right)^2}=5\)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(2+4\right)^2+\left(4+1\right)^2}=\sqrt{61}\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(2+4\right)^2+\left(-1+1\right)^2}=6\)
Ta có: \(BA^2+BC^2=5^2+6^2=25+36=61\)
\(AC^2=\left(\sqrt{61}\right)^2=61\)
Do đó: \(AC^2=BA^2+BC^2\)(=61)
Xét ΔABC có \(AC^2=BA^2+BC^2\)(cmt)
nên ΔABC vuông tại B(Định lí Pytago đảo)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{BA\cdot BC}{2}=\dfrac{5\cdot6}{2}=\dfrac{30}{2}=15\left(cm^2\right)\)
Đúng 0
Bình luận (0)
29 tháng 11 2021 lúc 13:45
Trong mặt phẳng toạ độ vẽ tam giác ABC với các đỉnh A(3; 5); B(3; -1); C(-5; -1). Tam giác ABC là tam giác gì?
Trong mặt phẳng toạ độ vẽ tam giác ABC với các đỉnh A(3; 5); B(3; -1); C(-5; -1). Tam giác ABC là tam giác gì?
Trong mặt phẳng toạ độ Oxy cho tam giác ABC nội tiếp đường tròn tâm I và D là chân đường phân giác trong đỉnh A của tam giác ABC biết toạ độ các đieemr A(2;6) I(-1/2;1) D(2;-3/2) biết phương trình tổng quát của đường thẳng BC
Trong mặt phẳng toạ độ vẽ tam giác ABC với các đỉnh A(-3;4); B(-3;1); C(1;-1)
Ta có hình vẽ tam giác ABC
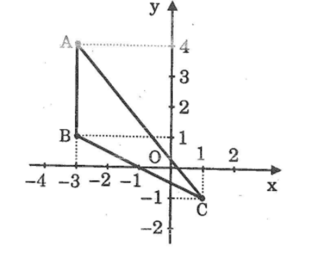
A(-3;4); B(-3;1); C(1;-1)
Đúng 0
Bình luận (0)
Vẽ tam giác ABC trên mặt phẳng toạ độ, biết A(0;3) ; B(4;0) ; C(1;1)
Tính diện tích tam giác ABC
SABC = SOAB - SOAC -SOBC
= 3.4 /2 - 3.1/2 - 4.1/2
= 6 - 1,5 - 2
= 2,5
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho 2 điểm A(1,2) và B(-3,1). Tìm toạ độ điểm C thuộc trục tung sao cho tam giác ABC vuông tại A. Tính diện tích tam giác ABC
Do C thuộc trục tung nên tọa độ có dạng \(C\left(0;c\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;-1\right)\\\overrightarrow{AC}=\left(-1;c-2\right)\end{matrix}\right.\)
Do tam giác ABC vuông tại A \(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\)
\(\Rightarrow4-\left(c-2\right)=0\Rightarrow c=6\)
\(\Rightarrow C\left(0;6\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(-1;4\right)\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{\left(-4\right)^2+\left(-1\right)^2}=\sqrt{17}\\AC=\sqrt{\left(-1\right)^2+4^2}=\sqrt{17}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{17}{2}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(-3,0); B(3,0); và C(2,6). Tìm toạ độ trục tâm H của tam giác ABC
Gọi \(H\left(x;y\right)\) là trực tâm tam giác
\(\Rightarrow\overrightarrow{AH}=\left(x+3;y\right)\) ; \(\overrightarrow{BH}=\left(x-3;y\right)\); \(\overrightarrow{BC}=\left(-1;6\right)\) ; \(\overrightarrow{AC}=\left(5;6\right)\)
Do H là trực tâm tam giác \(\Rightarrow\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-\left(x+3\right)+6y=0\\5\left(x-3\right)+6y=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-x+6y=3\\5x+6y=15\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{5}{6}\\\end{matrix}\right.\) \(\Rightarrow H\left(2;\dfrac{5}{6}\right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy cho tam giác ABC có : A(3,1) B(5,3) C(-1,1)
a) chứng tỏ tam giác ABC vuông cân
b) Tìm toạ độ của điểm M biết vecto MA - 2 vecto MB + 4 vecto MC = vector 0
c) tính diện tích tam giác ABC
d) Tìm N thuộc Oy để NB + NC nhỏ nhất