vào câu hỏi tương tự đi có lời giải r đó

thank you

Ta có \(\frac{AB}{AC}=\frac{7}{24}\Rightarrow\frac{AB}{7}=\frac{AC}{24}\)

\(\Rightarrow\frac{AB^2}{49}=\frac{AC^2}{576}=\frac{AB^2+AC^2}{49+576}=\frac{BC^2}{625}\)

\(\Rightarrow\frac{AB}{7}=\frac{AC}{24}=\frac{BC}{25}=\frac{112}{56}=2\)

\(\Rightarrow\) AB = 14 cm; AC = 48 cm; BC = 50 cm

1: AB/AC=5/7

=>HB/HC=(AB/AC)^2=25/49

=>HB/25=HC/49=k

=>HB=25k; HC=49k

ΔABC vuông tại A có AH là đường cao

nên AH^2=HB*HC

=>1225k^2=15^2=225

=>k^2=9/49

=>k=3/7

=>HB=75/7cm; HC=21(cm)

\(\dfrac{AB}{AC}=\dfrac{20}{21}\Rightarrow AB=\dfrac{20AC}{21}\)

Áp dụng hệ thức lượng:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{841}{400AC^2}\)

\(\Rightarrow AC=609\) \(\Rightarrow AB=\dfrac{20}{21}AC=580\)

\(BC=\sqrt{AB^2+AC^2}=841\)

Chu vị: \(609+580+841=2030\)

Ta có: \(\dfrac{AB}{AC}=\dfrac{20}{21}\)

nên \(AB=\dfrac{20}{21}\cdot AC\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\dfrac{1}{\dfrac{400}{441}AC^2}+\dfrac{\dfrac{400}{441}}{\dfrac{400}{441}AC^2}=\dfrac{1}{176400}\)

\(\Leftrightarrow\dfrac{400}{441}AC^2=336400\)

\(\Leftrightarrow AC^2=370881\)

hay AC=609(cm)

\(\Leftrightarrow AB=\dfrac{20}{21}\cdot AC=\dfrac{20}{21}\cdot609=580\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=580^2+609^2=371461\)

hay BC=841(cm)

Chu vi tam giác ABC là:

AB+AC+BC=580+609+841=2030(cm)

Chiều cao HI = 24cm nha mình nhầm

Xét tam giác ABC vuông tại A:

\(BC^2=AB^2+AC^2\left(Pytago\right)\)

\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{20^2+15^2}=25\left(cm\right)\)

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A:

\(AH.BC=AB.AC\)

\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{20.15}{25}=12\left(cm\right)\)

Ta có: \(P_{ABC}=AB+AC+BC=20+15+25=60\left(cm\right)\)

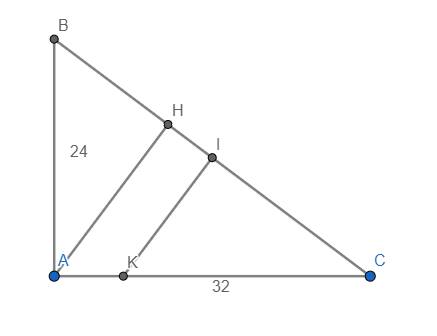
Ta có \(\widehat{HAC}=\widehat{B}\) (cùng phụ với \(\widehat{C}\)) 

Mà \(\widehat{B}=\tan^{-1}\left(\dfrac{AC}{AB}\right)=\tan^{-1}\left(\dfrac{32}{24}\right)=\tan^{-1}\left(\dfrac{4}{3}\right)\approx53,13^o\)

Nên \(\widehat{HAC}\approx53,13^o\)

Ta có \(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40\) cm

\(\Rightarrow IB=IC=20cm\)

Ta có \(CH=\dfrac{AC^2}{BC}=\dfrac{32^2}{40}=25,6cm\) 

\(AH=\dfrac{AB.AC}{BC}=\dfrac{24.32}{40}=19,2cm\)

Do vậy \(\dfrac{CI}{CH}=\dfrac{IK}{AH}\Rightarrow IK=\dfrac{CI.AH}{CH}=\dfrac{20.19,2}{25,6}=15cm\)

Mặt khác \(\dfrac{CI}{CH}=\dfrac{CK}{CA}\Rightarrow CK=\dfrac{CI.CA}{CH}=\dfrac{20.32}{25,6}=25cm\)

\(\Rightarrow C_{CIK}=CI+CK+IK\) \(=20+15+25=60cm\)

Mặt khác, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.24.32=384cm^2\)

Lại có \(\Delta CIK~\Delta CAB\left(g.g\right)\) \(\Rightarrow\dfrac{S_{CIK}}{S_{CAB}}=\left(\dfrac{IK}{AB}\right)^2=\left(\dfrac{15}{24}\right)^2=\dfrac{25}{64}\)

\(\Rightarrow S_{CIK}=\dfrac{25}{64}S_{CAB}=\dfrac{25}{64}.384=150cm^2\)