Cho (O) và điểm A nằm ngoài (O). Kẻ tiếp tuyến AC và AB tới đường tròn, AO cắt (O) tại I. Từ B vẽ đường song song với AO, đường này cắt (O) tại M. Tính số đo cung CM

Những câu hỏi liên quan
cho (O;R) từ A nằm ngoài đường tròn kẻ 2 tiếp tuyến AB và AC .Qua B kẻ đường thẳng song song với AO cắt (O) tại M .AM cắt (O) tại N. BN cắt AO tại I ,AO cắt BC tại K a) ABOC nội tiếp b)IA^2 = IN . IB
a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔIAN và ΔIBA có
góc IAN=góc IBA
góc AIN chung
=>ΔIAN đồng dạng với ΔIBA
=>IA^2=IN*IB
Đúng 0
Bình luận (1)
cho (O;R) từ A nằm ngoài đường tròn kẻ 2 tiếp tuyến AB và AC .Qua B kẻ đường thẳng song song với AO cắt (O) tại M .AM cắt (O) tại N. BN cắt AO tại I ,AO cắt BC tại K a) ABOC nội tiếp b)IA^2 = IN . IB
Cho đường tròn (O;R). Từ điểm A ngoài đường tròn kẻ các tiếp tuyến AB,AC với đường tròn (B,C là tiếp điểm). Gọi H là giao điểm của AO và BC
a) Cm: AO vuông góc với BC tại H
b) Vẽ đường kính BD của (O), cm: DC song song AO
c) AD cắt (O) tại E (E khác D). CM AE.AD=AH.AO
d) Qua vẽ đường thẳng vuông góc với AB. Đường thẳng này cắt OC tại F. CM: OA^2 = 2OC.OF
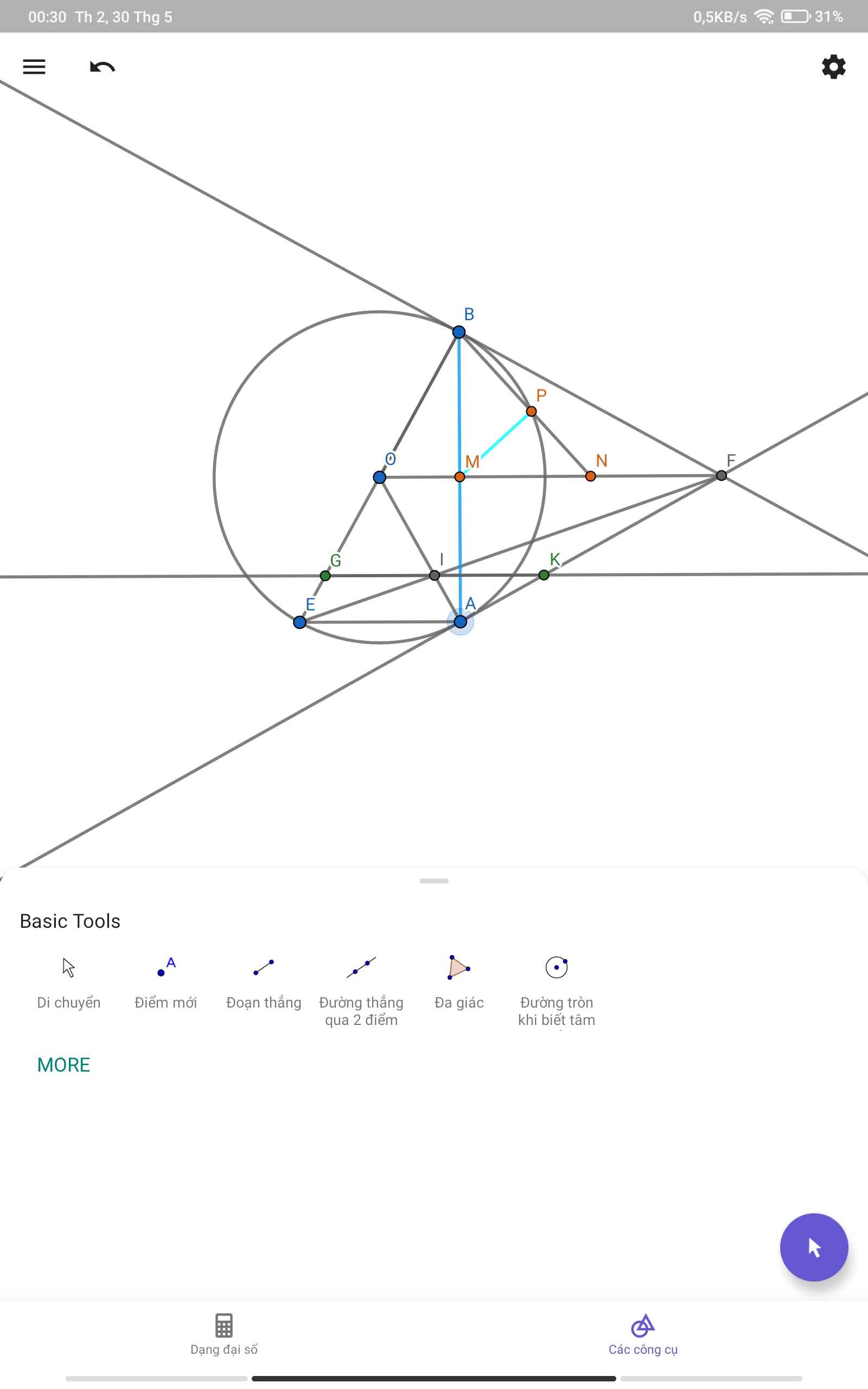
Đề:Câu 4 (3,0 điểm) Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA và FB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE tại G.a) Chứng minh tứ giác AOBF nội tiếp b) Chứng minh I là trung điểm của KGCâu 4 (3,0 điểm)Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA vàFB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE c...
Đọc tiếp
Đề:Câu 4 (3,0 điểm) Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA và FB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE tại G.
a) Chứng minh tứ giác AOBF nội tiếp
b) Chứng minh I là trung điểm của KGCâu 4 (3,0 điểm)
Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA và
FB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE
cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE tại G.
a) Chứng minh tứ giác AOBF nội tiếp
b) Chứng minh I là trung điểm của KG
c) Gọi M là giao của AB và OF, N là trung điểm của FM, NB cắt đường tròn (O) tại
P ( P khác B). Chứng minh PM vuông góc với NBc) Gọi M là giao của AB và OF, N là trung điểm của FM, NB cắt đường tròn (O) tại P ( P khác B). Chứng minh PM vuông góc với NB —->Giải câu b và c thôi nha

Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA và FB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE tại G.
a) Chứng minh tứ giác AOBF nội tiếp
b) Chứng minh I là trung điểm của KG
c) Gọi M là giao của AB và OF, N là trung điểm của FM, NB cắt đường tròn (O) tại P ( P khác B). Chứng minh PM vuông góc với NB
Đọc tiếp
Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA và FB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE tại G.
a) Chứng minh tứ giác AOBF nội tiếp
b) Chứng minh I là trung điểm của KG
c) Gọi M là giao của AB và OF, N là trung điểm của FM, NB cắt đường tròn (O) tại P ( P khác B). Chứng minh PM vuông góc với NB
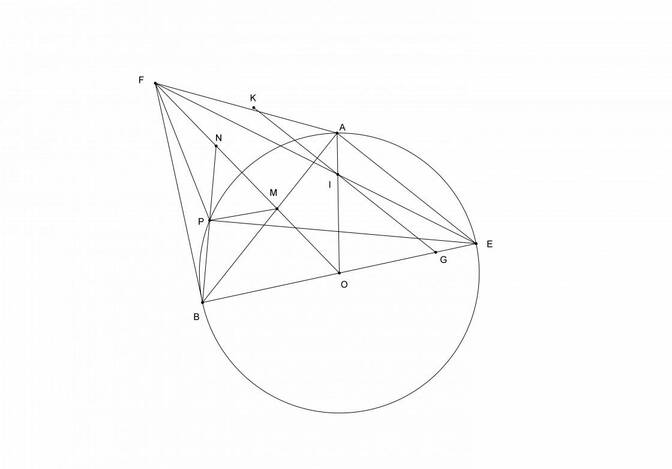
a. Tứ giác AOBF nội tiếp vì có $\angle OAF=\angle OBF=90^o$
b. Chú ý rằng $OF\perp AB$ nên $OF\parallel AE$, ta biến đổi tỉ số bằng định lý Thales:
\(\dfrac{IK}{OF}=\dfrac{AK}{AF}=\dfrac{EG}{EO}=\dfrac{IG}{OF}\), vậy $IK=IG$
c. Nếu mình không nhầm thì PM không vuông NB, vì khi đó $M,P,E$ thẳng hàng, bạn có thể kiểm tra hình vẽ của mình :c
Đúng 0
Bình luận (0)
Từ điểm A nằm ở bên ngoài đường tròn vẽ hai tiếp tuyến AB và AC .H là giao điểm của AO và BC .Kẻ dây BD song song với AO. đường thẳng AD cắt đường tròn O tại điểm thứ hai là E.kẻ BE cắt AO tại K Cm a)tứ giác ABOC nôi tiếp b)AK^2=KE.KB
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Câu 4
Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA và
FB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE
cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE tại G.
a) Chứng minh tứ giác AOBF nội tiếp
b) Chứng minh I là trung điểm của KG
c) Gọi M là giao của AB và OF, N là trung điểm của FM, NB cắt đường tròn (O) tại
P ( P khác B). Chứng minh PM vuông góc với NB
(Giải câu b và c thôi nha ) UwU
Đọc tiếp
Câu 4
Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Từ F kẻ các tiếp tuyến FA và
FB với đường tròn (O) ( A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE
cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE tại G.
a) Chứng minh tứ giác AOBF nội tiếp
b) Chứng minh I là trung điểm của KG
c) Gọi M là giao của AB và OF, N là trung điểm của FM, NB cắt đường tròn (O) tại
P ( P khác B). Chứng minh PM vuông góc với NB
(Giải câu b và c thôi nha ) UwU
ho đường tròn (O;R) . từ điểm A bên ngoài đường tròn lẻ các tiếp tuyến AB,AC với (O) (B , C là 2 tiếp điểm) . Gợi H là giao điểm của AO và BC. a, CM: AO vuông với Bc tại H b, kẻ đường lính BD của (O) . CM : DC song song với AO c, AD cắt (O) tại K ( K khác D). CM IH . AJ = AI.HJ
Xem chi tiết
Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Tử F kẻ các tiếp tuyến FA,
FB với đường tròn (O) (A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE
tại G.
a) Chứng minh tứ giác AOBF nội tiếp
b) Chứng minh I là trung điểm của KG
c) Gọi M là giao điểm của AB và OF, N là trung điểm của FM, NB cắt (O) tại P(P khác B). CÚng minh rằng PMperp NE
Đọc tiếp
Cho đường tròn (O) và điểm F nằm ngoài đường tròn. Tử F kẻ các tiếp tuyến FA,
FB với đường tròn (O) (A, B là các tiếp điểm). Vẽ đường kính BE của đường tròn (O), FE cắt AO tại I. Qua I vẽ đường thẳng song song với AE cắt AF tại K, cắt BE
tại G.
a) Chứng minh tứ giác AOBF nội tiếp
b) Chứng minh I là trung điểm của KG
c) Gọi M là giao điểm của AB và OF, N là trung điểm của FM, NB cắt (O) tại P(P khác B). CÚng minh rằng \(PM\perp NE\)
a/
Ta có A và B cùng nhìn FO dưới 1 góc vuông => A và B thuộc đường tròn đường kính FO
=> AOBF là tứ giác nội tiếp
b/
Ta có
\(\widehat{BAE}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow AE\perp AB\) (1)
\(FO\perp AB\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm đường tròn vuông góc và chia đôi dây cung nối 2 tiếp điểm) (2)
Từ (1) và (2) => AE//FO mà KG//AE (gt) => AE//KG//FO
\(\Rightarrow\dfrac{FK}{FA}=\dfrac{OG}{OE}\) (Talet) (1)
Xét tg AFE có
\(\dfrac{FK}{FA}=\dfrac{IK}{AE}\) (Talet trong tam giác) (2)
Xét tg OAE có
\(\dfrac{OG}{OE}=\dfrac{IG}{AE}\) (Talet trong tam giác) (3)
Từ (1) (2) (3) \(\Rightarrow\dfrac{IK}{AE}=\dfrac{IG}{AE}\Rightarrow IK=IG\)
c/ Câu này mình nghĩ bạn nên kiểm tra lại đề bài
Đúng 4
Bình luận (0)