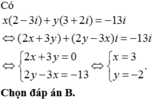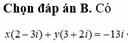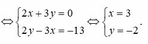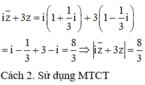giá trị lớn nhất của biểu thức B: \(\frac{3}{5}-3.I2x-13I\)
Tìm giá trị lớn nhất của biểu thức :B=-Ix-7I-Iy+13I+1945
b) B=-|x-7| - |y+13|+1945
Ta thấy: -|x-7| và -|y-5| ≤ 0 (với ∀ x,y) ⇒ -|x-7| - |y+13|+1945 ≤ 1945
Dấu "=" xảy ra khi x= 7 và y= 5
Vậy GTLN của B là 1945 tại x= 7 và y= 5
học tốt
Tìm các số thực x, y thoả mãn x(2-3i)+y(3+2i)=-13i, với i là đơn vị ảo.
A.x=-2,y=3
B.x=3,y=-2
C.x=3,y=2
D.x=-2,y=-3
Tính giá trị của biểu thức sau:
a) 2763 + 152
b) (-7) + (-14)
c) (-35) + 35
d) (-5) + (-248)
e) (-23) + 105
f) 78 + (-123)
g) 23 + (-13)
h) (-23) + 13
i) 26 + (-6)
j) 12 – 34
k) -23 – 47
l) 31 – (-23)
m) -9 – (-5)
n) 6 – (8 – 17)
o) 19 + (23 – 33)
p) (-12 – 44) + (-3)
q) 4 – (-15) –(-25)
r) -7 -14 – 26 –(-28)
a) 2763 + 152=2915
b) (-7) + (-14)=-21
c) (-35) + 35=0
d) (-5) + (-248)=-253
e) (-23) + 105=82
f) 78 + (-123)=-45
g) 23 + (-13)=10
h) (-23) + 13=-10
i) 26 + (-6)=20
j) 12 – 34=-22
k) -23 – 47=-70
l) 31 – (-23)=54
m) -9 – (-5)=-4
n) 6 – (8 – 17)=15
o) 19 + (23 – 33)=9
p) (-12 – 44) + (-3)=-59
q) 4 – (-15) –(-25)=44
r) -7 -14 – 26 –(-28)=-19
Đúng 0
Bình luận (0)
Tìm các số thực x, y thoả mãn
x
2
-
3
i
+
y
3
+
2
i
-
13
i
với i là đơn vị ảo.
Đọc tiếp
Tìm các số thực x, y thoả mãn x 2 - 3 i + y 3 + 2 i = - 13 i với i là đơn vị ảo.
GTNN của biểu thức M= Ix+3I + Ix-5I
GTNN của A= Ix+13I + 64
Giá trị của x thỏa mãn: 5x + 5x+2 = 3250
15 tháng 5 2022 lúc 14:08
Cho hai số phức z_1,z_2 thỏa mãn left|z_1+3+2iright|1 và left|z_2+2-iright|1. Xét các số phức za+bi, (a,bin R) thỏa mãn 2a-b0. Khi biểu thức Tleft|z-z_1right|+left|z-2z_2right| đạt giá trị nhỏ nhất thì giá trị biểu thức Pa^2+b^2 bằng?
Đọc tiếp
Cho hai số phức \(z_1,z_2\) thỏa mãn \(\left|z_1+3+2i\right|=1\) và \(\left|z_2+2-i\right|=1\). Xét các số phức \(z=a+bi\), (\(a,b\in R\)) thỏa mãn \(2a-b=0\). Khi biểu thức \(T=\left|z-z_1\right|+\left|z-2z_2\right|\) đạt giá trị nhỏ nhất thì giá trị biểu thức \(P=a^2+b^2\) bằng?
Cho số phức
z
1
-
1
3
i
. Tính
i
→
z
+
3
z
A.
i
→
z
+
3
z
8
3
B....
Đọc tiếp
Cho số phức z = 1 - 1 3 i . Tính i → z + 3 z
A. i → z + 3 z = 8 3
B. i → z + 3 z = 64 9
A. i → z + 3 z = 8 3
D. i → z + 3 z = 10 3
Cho số phức z thỏa mãn
z
2
−
i
+
13
i
1.
Tính môđun của số phức z A.
z
34
B.
z
5
34
3
C.
z...
Đọc tiếp
Cho số phức z thỏa mãn z 2 − i + 13 i = 1. Tính môđun của số phức z
A. z = 34
B. z = 5 34 3
C. z = 34 3
D. z = 34
Đáp án D
Phương pháp giải:
Tìm số phức z bằng phép chia số phức, sau đó tính môđun hoặc bấm máy tính
Lời giải:
Ta có
z 2 − i = 1 − 13 i ⇔ z = 1 − 13 i 2 − i = 3 + 5 i ⇒ z = 34
Đúng 0
Bình luận (0)
SGK Cánh Diều
13 tháng 8 2023 lúc 20:57
Luyện tập – Vận dụng 1
Tính giá trị của biểu thức: \(M = {\left( {\frac{1}{3}} \right)^{12}}.{\left( {\frac{1}{{27}}} \right)^{ - 5}} + {\left( {0,4} \right)^{ - 4}}{.25^{ - 2}}.{\left( {\frac{1}{{32}}} \right)^{ - 1}}\)
\(M=\left(\dfrac{1}{3}\right)^{12}\cdot\left(\dfrac{1}{3}\right)^{-15}+\left(\dfrac{2}{5}\right)^{-4}\cdot5^{-4}\cdot32\)
\(=\left(\dfrac{1}{3}\right)^{-3}+2^{-4}\cdot32\)
\(=27+\dfrac{32}{16}=27+2=29\)
Đúng 0
Bình luận (0)