cho tam giác DEF cân tại D. Gọi I là thung điểm của EF.
a/ cm tg DIE = tg DIF
b/ Kẻ IM vuông góc DE, IN vuông góc với DF
c/ cm MN song song EF
d/ cm 2xIN^2 = DF^2 - DN^2 - NF^2
( giờ mình chỉ cần câu d thôi, mấy bn giúp mình với )
Cho tam giác DEF cân tại D. Gọi I là trung điểm của EF. Kẻ IM vuông góc DE(M thuộc DE), IN vuông góc DF(N thuộc DF). a/ Chứng minh:Tam giác DIE=tam giác DIF, b/Tam giác IMN là tam giác cân, c/C/m:MN//EF, d/2*IN^2=DF^2-DN^2-NF^2
Cho tam giác ABC cân tại A. D là trung điểm của BC. Kẻ DE vuông góc với AB tại E; DF vuông góc với AC tại F
Chứng minh
a)TG DEB= Tg DFC
b) Tg AED=Tg AFD
c)Ad là phân giác của BAC^
d) AD là trung trực của EF
e) EF song song với BC
Cho tam giác DEF có DI là phân giác của góc D; I thuộc EF, ED=10 cm , DF=6 cm , FI= 4,8 cm. a) Tính EI b) Qua I kẻ đường thẳng song song với DF cắt DE tại M. Tính ME;MD;IM c) Chứng minh: DE/DF = ME/MD d) Gọi N là trung điểm của DF; DI cắt MN tại K; FM cắt IN tại H.Chứng minh: KH//MI
a: Xét ΔDEF có DI là phân giác
nên \(\dfrac{DE}{DF}=\dfrac{EI}{IF}\)
=>\(\dfrac{EI}{4,8}=\dfrac{10}{6}=\dfrac{5}{3}\)
=>EI=8(cm)
b: Ta có: EI+IF=EF
=>EF=6+8=14(cm)
Xét ΔEDF có MI//DF
nên \(\dfrac{MI}{DF}=\dfrac{EI}{EF}=\dfrac{EM}{ED}\)
=>\(\dfrac{MI}{6}=\dfrac{EM}{10}=\dfrac{6}{14}=\dfrac{3}{7}\)
=>\(MI=\dfrac{18}{7}\left(cm\right);EM=\dfrac{30}{7}\left(cm\right)\)
MD+ME=DE
=>MD+30/7=10
=>MD=40/7(cm)
c: Xét ΔDEF có DI là phân giác
nên \(\dfrac{EI}{IF}=\dfrac{ED}{DF}\left(1\right)\)
Xét ΔEDF có MI//DF
nên \(\dfrac{EI}{IF}=\dfrac{ME}{MD}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{ED}{DF}=\dfrac{ME}{MD}\)
cho tam giác ABC cân tại A . gọi D là trong điểm cạnh BC kẻ DE vuông góc với AB.
(EϵAB) DF vuông góc với AC (FϵAC)
a)CM: BE=CF
b)CM: tam giác DEF là tam giác cân
c)CM: EF song songBC
ét o ét giúp tui vs, ai làm đúng tui tick nha
`@` `\text {dnammv}`
`a,`
Xét \(\Delta BED\) và \(\Delta CFD\) có:
\(\left\{{}\begin{matrix}\text{BD = CD (D là trung điểm của BC}\\\widehat{\text{B}}=\widehat{\text{C}}\left(\text{ }\Delta\text{ABC cân tại A}\right)\\\widehat{BED}=\widehat{CFD}\left(=90^0\right)\end{matrix}\right.\)
`=> \Delta BED = \Delta CFD (ch-gn)`
`-> \text {BE = CF (2 cạnh tương ứng)}`
`b,`
Vì `\Delta BED = \Delta CFD (a)`
`-> \text {DE = DF (2 cạnh tương ứng)}`
`\text {Xét}` `\Delta DEF:`
`\text {DE = DF}`
`-> \Delta DEF` là `\Delta` cân
`c,`
Vì \(\left\{{}\begin{matrix}\text{AB = AC (tam giác ABC cân tại A)}\\\text{BE = CF (a)}\end{matrix}\right.\)
`-> \text {AE = AF}`
\(\text{Xét }\Delta\text{ AEF}: \)
`\text {AE = AF}`
`-> \Delta AEF` là `\Delta` cân (tại A).
`->`\(\widehat {AEF}= \widehat {AFE}\)\(=\dfrac{180-\widehat{A}}{2}\text{ }\left(1\right)\)
`\Delta ABC` cân tại `A`
`->`\(\widehat {ABC}= \widehat {ACB}=\)\(\dfrac{180-\widehat{A}}{2}\text{ }\left(2\right)\)
Từ `(1)` và `(2)`
`->`\(\widehat {AEF}= \widehat {ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {EF // BC (tính chất 2 đường thẳng //).}`
Cho tam giác DEF cân tại D. Gọi I là trung điểm của EF
a, Chứng minh: Tam giác DIE = Tam giác DIF
b, Kẻ ID vuông góc DE ( M thuộc DE), IN vuông góc DF ( N thuộc DF). Chứng minh Tam giác IMN là tam giác đều
c, Chứng minh MN//EF
d, Chứng minh: 2.IN^2 = DF^2 - DN^2 - NF^2
Giúp mk với!
cho tam giác DEF cân tại D. Đường cao DH(H thuộc EF). Trên tia đối EF, lấy điểm M sao cho EM=ED. Kẻ EI vuông góc MD(I thuộc MD).
a)CM tg HDM đồng dạng tg IEM
b)Tia IH cắt tia DF tại N. CM FH=FN
d)ĐK của tg DEF để H là trung điểm của IN
Cho tam giác DEF vuông tại D. Trên tia đối của DF lấy điểm M sao cho DM = DF a, cho DE= 9cm, DF = 12 cm, tính EF b, CM ∆DEM= ∆DEF c, kẻ DH vuông góc với ME, DK vuông góc với EF, cm ∆HEK cân d, CM HD // EF
a) Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:
\(EF^2=DE^2+DF^2\)
\(\Leftrightarrow EF^2=9^2+12^2=225\)
hay EF=15(cm)
Vậy: EF=15cm
a) Xét tam giác EDF có: EF2 = DE2 + DF2 (đ/lí py-ta-go)
=> EF2 = 92 + 122
=> EF2 = 81 + 144 = 225
=> EF = 112,5 cm
b) Xét tam giác DEM và tam giác DEF có :
EDM = EDF = 1v
ED chung
DM = DF (gt)
=> tam giác DEM = tam giác DEF (c.g.c) hay (c/huyền+c/góc vuông)
Bài 1 : Cho tam giác ABC cân tại A vẽ AD ^ BC ( D thuộc BC)
a) Chứng minh BD = CD
b) Vẽ DH cắt AB tại H và DK cắt AC tại K . Chứng minh DH = Dk
c) Chứng minh HK // BC
d) Cho AB = 10 cm ; BC = 12 cm. Tính AD
Bài 2: Cho tam giác DEF có DE = DF = 5cm, EF= 6 cm . Gọi I là trung điểm của EF
a) Chứng minh tam giác DEI = tam giác DFI
b) Tính độ dài đoạn DI
c) Kẻ IH vuông góc với DE ( H thuộc DE) . Kẻ IJ vuông góc với DF ( J thuộc DF). Chứng minh : tam giác IHJ là tam giác cân
d) Chứng minh HJ song song EF
Mọi người ơi giúp em với ạ !
tu ve hinh :
cau b la vuong goc phai k
a, tamgiac ABC can tai A(gt) => AB = AC va goc ABC = goc ACB (dn)
goc ADB = goc ADC do AD | BC (GT)
=> tamgiac ADB = tamgiac ADC (ch - gn)
=> BD = DC (dn)
b, xet tamgiac BHD va tamgiac CKD co : BD = DC (Cau a)
goc ABC = goc ACB (cau a)
goc BHD = goc DKC = 90 do HD | AB va HK | AC (gt)
=> tamgiac BHD = tamgiac CKD (ch - gn)
=> HD = DK (dn)
c, xet tamgiac AHD va tamgiac AKD co : AD chung
HD = DK (cau b)
goc AHD = goc AKD = 90 do HD | AB va HK | AC (gt)
=> tamgiac AHD = tamgiac AKD (ch - cgv)
=> tamgiac AHK can tai A (dn)
=> goc AHK = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc AHK = goc ABC 2 goc nay dong vi
=> HK // BC (tc)
d, tu ap dung py-ta-go
a, tamgiac ABC can tai A(gt) => AB = AC va goc ABC = goc ACB (dn)
goc ADB = goc ADC do AD | BC (GT)
=> tamgiac ADB = tamgiac ADC (ch - gn)
=> BD = DC (dn)
b, xet tamgiac BHD va tamgiac CKD co : BD = DC (Cau a)
goc ABC = goc ACB (cau a)
goc BHD = goc DKC = 90 do HD | AB va HK | AC (gt)
=> tamgiac BHD = tamgiac CKD (ch - gn)
=> HD = DK (dn)
c, xet tamgiac AHD va tamgiac AKD co : AD chung
HD = DK (cau b)
goc AHD = goc AKD = 90 do HD | AB va HK | AC (gt)
=> tamgiac AHD = tamgiac AKD (ch - cgv)
=> tamgiac AHK can tai A (dn)
=> goc AHK = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc AHK = goc ABC 2 goc nay dong vi
=> HK // BC (tc)
d, tu ap dung py-ta-go
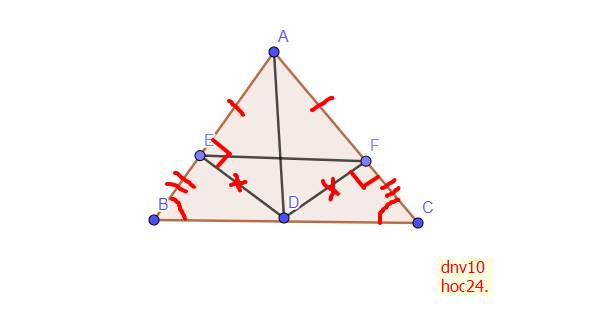
Cho tam giác ABC cân tại A. Gọi I là trung điểm cạnh BC, kẻ ID vuông góc với AB tại D, kẻ IE vuông góc với AC tại E.
a) CM: tam giác ABI = tam giác ACI.
b) CM: tam giác BDI = tam giac CEI
c) CM: DE song song với BC
d) CM: AB^2 = AD^2 + BD^2 + 2DI^2
Mình làm phần d) thôi nhé!
Theo phần a) ta có được: \(\widehat{AIB}=\widehat{AIC}\)(2 góc tương ứng:
Tam giác ABI = Tam giác ACI)
mà \(\widehat{AIB}+\widehat{AIC}=180\)(2 góc kề bù)
=>\(\widehat{AIB}=\widehat{AIC}=90\)
Xét tam giác ABI vuông tại I, áp dụng định lí py-ta-go ta có:
\(AB^2=AI^2+BI^2\)(1)
Xét tam giác ADI vuông tại D, áp dụng định lí py-ta-go ta có:
\(AI^2=AD^2+DI^2\)(2)
Xét tam giác BDI vuông tại D, áp dụng định lí py-ta-go ta có:
\(BI^2=DI^2+BD^2\)(3)
Thay (2),(3) vào (1) ta có được:
\(AB^2=AD^2+DI^2+DI^2+BD^2\)
(hay) \(AB^2=AD^2+BD^2+2DI^2\)(ĐPCM)