1. Cho tứ diện ABCD có các cặp cạnh đối bằng nhau từng đôi một \(AB=CD,AC=BD,BC=AD\) Chứng minh với mọi điểm M trong không gian ta đều có \(MA^2+MB^2+MC^2\ge MD^2\)

Những câu hỏi liên quan
Cho tứ giác ABCD và một điểm M thuộc miền trong của tứ giác . Chứng minh BĐT :
a) MA + MB + MC + MD >= 1/2 *(AB+BC+CD+DA)
b) MA+MB+MC+MD >= AC+BD. Dấu "=" xảy ra khi nào?
a/ Áp dụng BĐT ba điểm :
\(AM+MB\ge AB\) ; \(BM+MC\ge BC\); \(CM+MD\ge CD\) ; \(DM+MA\ge DA\)
Cộng theo vế : \(2\left(MA+MB+MC+MD\right)\ge AB+BC+CD+DA\)
\(\Leftrightarrow MA+MB+MC+MD\ge\frac{AB+BC+CD+DA}{2}\)
Đẳng thức xảy ra khi M là giao điểm của AC và BD
b/ Ta cũng áp dụng BĐT ba điểm :
\(AM+MC\ge AC\) ; \(BM+MD\ge BD\)
Cộng theo vế : \(MA+MB+MC+MD\ge AC+BD\)
Đẳng thức xảy ra khi M là giao điểm của AC và BD
Đúng 0
Bình luận (0)
cho tứ giác ABCD và điểm M thuộc đường trong của tứ giác
Chứng minh : a) MA+MB+MC+MD > AB+CD
b) MA+MB+MC+MD \(\ge\dfrac{AB+BC+CD+DA}{2}\)
Hình bạn tự vẽ nhé.
a) Theo bất đẳng thức tam giác:
MA+MB> AB (1)
MC+MD>CD (2)
=> MA +MB +MC +MD >AB +CD
b) Theo BĐT tam giác:
MA+MD > AD (3)
MB +MC >BC (4)
(1)(2)(3)(4) => 2(MA +MB+MC+MD)>AB +BC +CD +AD
MA +MB +MC +MD>AB +BC +CD +AD /2
Mình không nghĩ là dấu≥ vì bất đẳng thức tam giác đâu có dấu bằng đâu nhỉ?
Đúng 1
Bình luận (2)
Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh MN ⊥ AB và MN ⊥ CD. Mặt phẳng (CDM) có vuông góc với mặt phẳng (ABN) không? Vì sao?
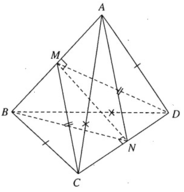
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó MN ⊥ CD vì N là trung điểm của CD. Tương tự ta chứng minh được NA = NB và suy ra MN ⊥ AB. Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.
Đúng 0
Bình luận (0)
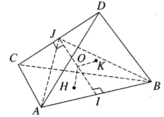
Cho tứ diện ABCD có AD = BC = a, BD = CA = b, CD = AB = c. Chứng minh rằng các đường vuông góc chung của các cặp cạnh đối diện đồng quy và đôi một vuông góc với nhau
Gọi I và J lần lượt là trung điểm của AB và CD. Vì ΔACD = ΔBDC nên các tiếp tuyến tương ứng của chúng bằng nhau, do đó AJ = BJ. Từ đó suy ra IJ ⊥ AB. Tương tự, IJ ⊥ CD. Vậy IJ là đường vuông góc chung của AB và CD.
Làm tương tự đối với các cặp cạnh đối diện khác ta chứng minh được rằng đường nối trung điểm của các cặp cạnh đối diện là đường vuông góc chung của cặp cạnh đó. Do đó các đường đó đồng quy tại O là trung điểm của mỗi đường.
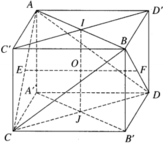
Gọi (P) là mặt phẳng qua AB và song song với CD, (Q) là mặt phẳng qua CD và song song với AB; A', B' lần lượt là hình chiếu vuông góc của A, B lên (Q); C', D' lần lượt là hình chiếu vuông góc của C, D lên (P). Dễ thấy AC'BD'.A'CB'D là hình hộp chữ nhật. Đường nối hai tâm của mỗi cặp mặt đối diện của hình hộp chữ nhật đó chính là đường vuông góc chung của các cặp cạnh đối diện của tứ diện ABCD. Do đó chúng đôi một vuông góc với nhau.
Đúng 1
Bình luận (0)
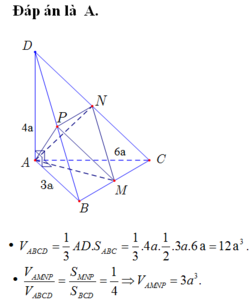
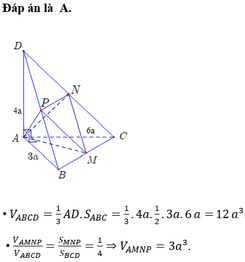
Cho tứ diện ABCD có các cạnh AB,AC, AD vuông góc với nhau từng đôi một và AB3a, AC6a, AD4a. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, BD. Tính thể tích khối đa diện AMNP.
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB,AC, AD vuông góc với nhau từng đôi một và AB=3a, AC=6a, AD=4a. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, BD. Tính thể tích khối đa diện AMNP.
![]()
![]()
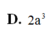
Cho tứ diện ABCD có các cạnh AB,AC,AD vuông góc với nhau từng đôi một và AB3a,AC6a,AD4a. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CD,BD . Tính thể tích khối đa diện AMNP A. 3
a
3
B. 12
a
3
C.
a
3
D. 2
a
3
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB,AC,AD vuông góc với nhau từng đôi một và AB=3a,AC=6a,AD=4a. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CD,BD . Tính thể tích khối đa diện AMNP
A. 3 a 3
B. 12 a 3
C. a 3
D. 2 a 3
Cho tứ diện ABCD có AB=CD=a, AC=BD=b, AD=BC=c
a, chứng minh: các đoạn nối trung điểm các cặp cạnh đối diện thì vuông góc với 2 cạnh đó
b, Tính cos góc giữa 2 đường thẳng AC và BD
Cho tứ diện ABCD có AB=CD=a, AC=BD=b, AD=BC=c
a, chứng minh: các đoạn nối trung điểm các cặp cạnh đối diện thì vuông góc với 2 cạnh đó
b, Tính cos góc giữa 2 đường thẳng AC và BD
Cho tứ diện ABCD có AB=CD=a, AC=BD=b, AD=BC=c
a, chứng minh: các đoạn nối trung điểm các cặp cạnh đối diện thì vuông góc với 2 cạnh đó
b, Tính cos góc giữa 2 đường thẳng AC và BD