Chöùng minh các ñöôøng thaúng sau, luoân ñi qua moät ñieåm coá ñònh khi m thay ñoåi
(d) : mx – y = 3m + 2 (d) : 2 mx + y = (3m – 2) – 2x
(d) : y = 3mx + m + 2 (d) : (m – 3)x – 3y = m + 2010
Chứng minh các đường thẳng sau luôn đi qua một điểm cố định khi m thay đổi:
(d) : mx – y = 3m + 2 (d) : 2 mx + y = (3m – 2) – 2x
(d) : y = 3mx + m + 2 (d) : (m – 3)x – 3y = m + 2010
Bài 1 : viết PT đường thẳng (d) đi qua 2 điểm
a, (2; 1) và (-1; -5)
b, (4; -1) và (3; 2)
Bài 2: cho 3 điểm A (2; 1), B (-1; 2), C (0; -1)
a, viết PT đường thẳng AB
b, chứng minh 3 điểm A, B, C thẳng hàng
c, tìm a, b để (d) : y = (2a - b) x +3a - 1 đi qua điểm B và C
Bài 3: chứng minh đường thẳng sau luôn đi qua 1 điểm cố định khi m thay đổi
a, mx - y = 3m + 2
b, 2 mx + y = (3m - 2) - 2x
Bài 4: tìm các giá trị của m để 3 đường thẳng sau đồng quy tại 1 điểm trong mặt phẳng tọa độ
a, 3x + 2y = 5; 2x - y = 4 và mx + 7y = 11
b, y = 2x + 3; y = x + 4; y = (3 - 5m) x - 5m
Tìm 3 đường thẳng sau đồng quy :
a, 2x - y=m ( d1)
x - y = 2m ( d2)
mx - ( m - 1)y = 2m - 1 ( d3)
b, mx + y = m2 + 1 ( d1)
( m + 2 )x - ( 3m + 5 )y = m - 5 ( d2)
( 2 - m )x - 2y = -m2 + 2m - 2 ( d3)
Help me !!!!
Giải và biện luận các hệ phương trình sau:
a) \(\left\{{}\begin{matrix}mx+y=3m-1\\x+my=m+1\end{matrix}\right.\) b) \(\left\{{}\begin{matrix}x+my=3m\\mx-y=m^2-2\end{matrix}\right.\)
c)\(\left\{{}\begin{matrix}x-my=1+m^2\\mx+y=1+m^2\end{matrix}\right.\) d) \(\left\{{}\begin{matrix}2x-y=3+2m\\mx+y=\left(m+1\right)^2\end{matrix}\right.\)
mk lm câu khó nhất trong các câu này , rồi bn làm tương tự với các câu còn lại nha .
d) ta có : \(\left\{{}\begin{matrix}2x-y=3+2m\\mx+y=\left(m+1\right)^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=2x-3-2m\\mx+2x-3-2m=m^2+2m+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2x-3-2m\\mx+2x=m^2+4m+4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=2x-3-2m\\\left(m+2\right)x=\left(m+2\right)^2\end{matrix}\right.\).....(1)
th1: \(m+2=0\Leftrightarrow m=-2\)
khi đó ta có : (1) \(\Leftrightarrow\left\{{}\begin{matrix}y=2x-3-2m\\0x=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\in R\\y=2x+1\end{matrix}\right.\)
\(\Rightarrow\) phương trình có vô số nghiệm
th2: \(m+2\ne0\Leftrightarrow m\ne-2\)
khi đó ta có : (1) \(\Leftrightarrow\left\{{}\begin{matrix}y=2x-3-2m\\x=m+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=m+2\\y=1\end{matrix}\right.\)
\(\Rightarrow\) phương trình có nghiệm duy nhất \(\left\{{}\begin{matrix}x=m+2\\y=1\end{matrix}\right.\)
vậy khi +) \(m=-2\) phương trình có vô số nghiệm
+) khi \(m\ne-2\) phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=m+2\\y=1\end{matrix}\right.\)
Cho hàm số y=-mx+4-3m(d)
a. Vẽ d với m=-1
b.Tìm m để d đi qua gốc toạ độ
c.Tìm m để d cắt trục tung tại điểm -4
d.Tìm m để d cắt trục tung tại điểm -2
e.Tìm m để d song song với đường thẳng y=2x+3
f.Tìm m để d đi qua điểm A(1;2)
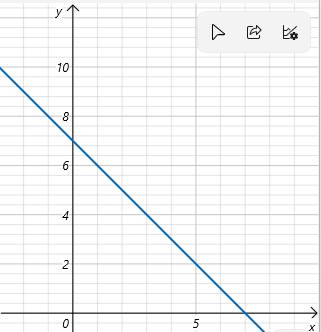
a, với d = -1
Ta có hàm số y = - \(x\) + 4 + 3 ⇒ y = -\(x\) + 7
+ Giao của đồ thị với trục o\(x\) là điểm có hoành độ thỏa mãn:
- \(x\) + 7 = 0 ⇒ \(x\) = 7
Giao đồ thì với trục o\(x\) là A(7; 0)
+ Giao của đồ thị với trục oy là điểm có tung độ thỏa mãn:
y = 0 + 7 ⇒ y = 7
Giao đồ thị với trục oy là điểm B(7; 0)
Ta có đồ thị
b, Đồ thị hàm số y = - m\(x\) + 4 - 3m (d)
(d) đi qua gốc tọa độ khi và chỉ tọa độ O(0; 0) thỏa mãn phương trình đường thẳng d
Thay tọa độ điểm O vào đường thẳng d ta có:
-m.0 + 4 - 3m = 0
4 - 3m = 0
m = \(\dfrac{4}{3}\)
c, để d cắt trục tung tại điểm - 4 khi và chỉ m thỏa mãn phương trình:
-m.0 + 4 - 3m = - 4
4 - 3m = - 4
3m = 8
m = \(\dfrac{8}{3}\)
d, d cắt trục tung tại điểm - 2 khi và chỉ khi m thỏa mãn phương trình
-m.0 + 4 - 3m = -2
4 - 3m = -2
3m = 6
m = 2
e, d song song với đường thẳng y = 2\(x\) + 3 khi và chỉ khi
- m = 2 và 4 - 3m ≠ 3 ⇒ m ≠ \(\dfrac{1}{3}\)
⇒m = -2
f, d đi qua A (1;2) khi và chỉ m thỏa mãn phương trình:
-m.(1) + 4 - 3m = 2
-m - 3m = 2 - 4
- 4m = -2
m = \(\dfrac{1}{2}\)
Giải và biện luận các phương trình sau a) {mx+(m+1)y=m+1
{2x+my=2
b) {mx+(m-2)y=5
{(m+2)x+(m+1)y=2
c){(m-1)x+2y=3m-1
{(m+2)x-y=1-m
a: \(\Leftrightarrow\left\{{}\begin{matrix}mx+\left(m+1\right)y=m+1\\my=2-2x\end{matrix}\right.\)
Nếu m=0 thì hệ sẽ là y=0+1=1 và 2-2x=0
=>y=1 và x=1
Nếu m<>0 thì \(\left\{{}\begin{matrix}y=\dfrac{-2x+2}{m}\\x\cdot m+\left(m+1\right)\cdot\dfrac{-2x+2}{m}=m+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\cdot m+x\cdot\dfrac{-2\left(m+1\right)}{m}+\dfrac{2m+2}{m}=m+1\\y=\dfrac{-2x+2}{m}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\cdot\left(m+\dfrac{-2m-2}{m}\right)=m+1-\dfrac{2m+2}{m}=\dfrac{m^2+m-2m-2}{m}=\dfrac{m^2-m-2}{m}\\y=\dfrac{-2x+2}{m}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\cdot\dfrac{m^2-2m-2}{m}=\dfrac{m^2-m-2}{m}\\y=\dfrac{-2x+2}{m}\end{matrix}\right.\)
Nếu m^2-2m-2=0 thì hệ vô nghiệm
Nếu m^2-2m-2<>0 thì hệ sẽ có nghiệm duy nhất là:
\(\left\{{}\begin{matrix}x=\dfrac{m^2-m-2}{m^2-2m-2}\\y=-\dfrac{2}{m}\cdot\dfrac{m^2-m-2}{m^2-2m-2}+\dfrac{2}{m}=\dfrac{-2m^2+2m+4+2m^2-4m-4}{m\left(m^2-2m-2\right)}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m-2}{m^2-2m-2}\\y=-\dfrac{2}{m^2-2m-2}\end{matrix}\right.\)
c: =>(m-1)x+2y=3m-1 và (2m+2)x-2y=2-2m
=>(3m+1)x=m+1 và y=(m+2)x+m-1
Nếu m=-1/3 thì hệ vô nghiệm
Nếu m<>-1/3 thì hệ sẽ có nghiệm duy nhất là:
\(\left\{{}\begin{matrix}x=\dfrac{m+1}{3m+1}\\y=\dfrac{m^2+3m+2}{3m+1}+m-1=\dfrac{m^2+3m+2+3m^2-3m+m-1}{3m+1}=\dfrac{4m^2+m+1}{3m+1}\end{matrix}\right.\)
Cho hàm số y=-x^3+m^2x^2+mx+3m+5. Tìm m để y'>0 trên đoạn có độ dài bằng 2 căn 2
Bài 1: Giải và biện luận các phương trình sau:
a) m(m-x)= 3(x+3)-6m
b) mx-3m=2x-3
c) (m^2 -9)x=m^2 +3m
Bài 2: Giải và biện luận các phương trình sau:
a) m(m-1)=2(2x+1)
b) (m^2 - 9)x=m^2 +3m
c) m(m-1)= 2(4-x)
d) (m^2 -3m+2)x= m-2
Các cậu giúp tớ với ạ, không cần làm hết đâu ạ, mng biết câu nào thì làm hộ tớ với nhé, plss!
Vì hai bài giống nhau nên anh sẽ làm mẫu bài 1 nhé.

Cho (P) y=2.\(x^2\) và (d) y=mx+1
Tìm m để (d) cắt (P) tại 2 điểm phân biệt A,B sao cho \(^{^SAOB}\) = \(\dfrac{3m}{2}\)
Lời giải:
PT hoành độ giao điểm:
$2x^2-mx-1=0(*)$
$\Delta=m^2+8>0$ với mọi $m$ đồng nghĩa $(P)$ và $(d)$ luôn cắt nhau tại 2 điểm $A,B$ phân biệt với mọi $m$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_A+x_B=\frac{m}{2}\\ x_Ax_B=-\frac{1}{2}\end{matrix}\right.\)
Khoảng cách từ $O$ đến $AB$ là:
$\frac{|m.0+1-0|}{\sqrt{m^2+1}}=\frac{1}{\sqrt{m^2+1}}$
$AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}$
$=\sqrt{(x_A-x_B)^2+(mx_A+1-mx_B-1)^2}$
$=\sqrt{(x_A-x_B)^2(m^2+1)}$
$=\sqrt{(x_A+x_B)^2-4x_Ax_B}.\sqrt{m^2+1}$
$=\sqrt{\frac{m^2}{4}+2}.\sqrt{m^2+1}$
$S_{OAB}=\frac{1}{2}\sqrt{\frac{m^2}{4}+2}.\sqrt{m^2+1}.\frac{1}{\sqrt{m^2+1}}=\frac{3m}{2}$
$m=\pm \sqrt{\frac{8}{35}}$