a) 22+x=52

x=52-22

x=30

b) 2x-3=45

2x=45+3

2x=48

x=48:2

x=24

c)4^x = 64

4x=4³

\(\Rightarrow x=3\)

a) 22+x=52

          x=52-22

          x=30

b) 2x-3=45

        2x=45+3

        2x=48

          x=48 : 2

          x=24

c) \(4^x=64\)

    \(4^x=4^3\)

=> x=3

\(a,22+x=52\)                                                               \(c,4^x=64\)

\(\Rightarrow x=52-22\)                                                            \(\Rightarrow4^x=4^3\)

\(\Rightarrow x=30\)                                                                        \(\Rightarrow x=3\)

\(b,2x-3=45\)

\(\Rightarrow2x=45+3\)

\(\Rightarrow2x=48\)

\(\Rightarrow x=\frac{48}{2}=24\)

a: Ta có: \(\left(x^2+x-1\right)^2-\left(x^2+2x+3\right)^2\)

\(=\left(x^2+x-1-x^2-2x-3\right)\left(x^2+x-1+x^2+2x+3\right)\)

\(=\left(-x-4\right)\left(2x^2+3x+2\right)\)

b: Ta có: \(\left(x-3\right)^2-16\)

\(=\left(x-3-4\right)\left(x-3+4\right)\)

\(=\left(x+1\right)\left(x-7\right)\)

c: \(y^2+16y+64=\left(y+8\right)^2\)

a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2

(Khi đó: x2 – 4 = (x + 2)(x – 2) ≠ 0)

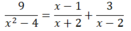
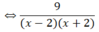
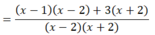
Vậy tập nghiệm của pt là: S = {-1; 1}

b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0

Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x

⇔ x = -5 hoặc x = 5/3

Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}

c) x – 2)2 + 2(x – 1) ≤ x2 + 4

⇔ x2 – 4x + 4 + 2x – 2 ≤ x2 + 4

⇔ -2x ≤ 2

⇔ x ≥ -1

Tập nghiệm S = {x | x ≥ -1}

\(\left|x\right|=2\Rightarrow\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)

Thay x=-2 vào B ta có:
\(B=4x^3+x-2022=4.\left(-2\right)^3+\left(-2\right)-2022=-32-2-2022=-2056\)

Thay x=2 vào B ta có:

\(B=4x^3+x-2022=4.2^3+2-2022=32+2-2022=-1988\)

-1988

b: Ta có: \(x^3-9x^2+27x-27\)

\(=\left(x-3\right)^3\)

\(=\left(-7\right)^3=-343\)

c: Ta có: \(\dfrac{x^3-1}{x^2+1}\)

\(=\dfrac{6^3-1}{6^2+1}=\dfrac{215}{37}\)

a)\(\left(2x+1\right)^3=5^3\)

\(\Rightarrow2x+1=5\)

\(2x=5-1\)

\(2x=4\)

\(x=4:2\)

\(x=2\)

\(b,\left(2x-1\right)^3=125\)

\(\Rightarrow2x-1=5\)

\(2x=5+1\)

\(2x=6\)

\(x=6:2=3\)

b) \(\left(2x-1\right)^3=125\)

\(\left(2x-1\right)^3=5^3\)

\(2x-1=5\)

\(2x=5+1\)

\(2x=6\)

\(x=6:2\)

\(x=3\)

c) \(4x^3+15=19\)

\(4x^3=19+15\)

\(4x^3=34\)

\(x^3=\frac{34}{4}=\frac{17}{2}\)

Chỗ này có vẻ hơi sai sai ạ :33

2:

a: Sửa đề: \(\dfrac{a^2+3}{\sqrt{a^2+2}}>2\)

\(A=\dfrac{a^2+3}{\sqrt{a^2+2}}=\dfrac{a^2+2+1}{\sqrt{a^2+2}}=\sqrt{a^2+2}+\dfrac{1}{\sqrt{a^2+2}}\)

=>\(A>=2\cdot\sqrt{\sqrt{a^2+2}\cdot\dfrac{1}{\sqrt{a^2+2}}}=2\)

A=2 thì a^2+2=1

=>a^2=-1(loại)

=>A>2 với mọi a

b: \(\Leftrightarrow\sqrt{a}+\sqrt{b}< =\dfrac{a\sqrt{a}+b\sqrt{b}}{\sqrt{ab}}\)

=>\(a\sqrt{a}+b\sqrt{b}>=a\sqrt{b}+b\sqrt{a}\)

=>\(\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)-\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)>=0\)

=>(căn a+căn b)(a-2*căn ab+b)>=0

=>(căn a+căn b)(căn a-căn b)^2>=0(luôn đúng)

1

ĐK: `x>1`

PT trở thành:

\(\sqrt{\dfrac{2x-3}{x-1}}=2\\ \Leftrightarrow\dfrac{2x-3}{x-1}=2^2=4\\ \Leftrightarrow4x-4-2x+3=0\\ \Leftrightarrow2x-1=0\\ \Leftrightarrow x=\dfrac{1}{2}\left(KTM\right)\)

Vậy PT vô nghiệm.

b

ĐK: \(x\ge2\)

Đặt \(t=\sqrt{x-2}\) (\(t\ge0\))

=> \(x=t^2+2\)

PT trở thành: \(t^2+2-5t+2=0\)

\(\Leftrightarrow t^2-5t+4=0\)

nhẩm nghiệm: `a+b+c=0` (`1+(-5)+4=0`)

\(\Rightarrow\left\{{}\begin{matrix}t=1\left(nhận\right)\\t=4\left(nhận\right)\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-2}=1\\\sqrt{x-2}=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3\left(TM\right)\\x=18\left(TM\right)\end{matrix}\right.\)

\(a=0;1;2;3\) ở câu a

\(a=0;1;2;3;4;5;6;7\) ở câu b

\(a=0;1;2;3;4;5;6\) ở câu c

a) a = 3

b) b = 8

c) x = 1

d) ab = 23

a: =>2x^3-4x^2-3x^2+6x+4x-8+a+8 chia hết cho x-2

=>a+8=0

=>a=-8

b: =>2x^3+x^2-x^2-0,5x-0,5x+0,25+m-0,25 chia hết cho 2x+1

=>m-0,25=0

=>m=0,25