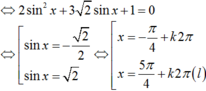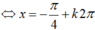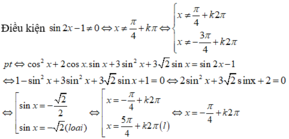3sinx= sinx

Những câu hỏi liên quan
(2sinx+cosx)(sinx+cosx) =3sinx +2cosx
Nếu sinx + cosx = 1/2 thì 3sinx + 2cosx bằng
![]()
![]()
![]()
![]()
Chọn A.
Ta có:
sinx + cosx = ½ nên ( sinx + cosx)2 = ¼
Do đó sinx. cosx = -3/8
Khi đó sinx; cosx là nghiệm của phương trình
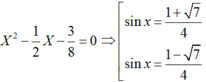
Ta có sinx + cos x = ½ nên 2( sinx + cosx) = 1
+) Với 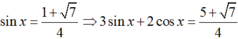
+) Với 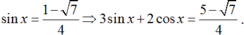
Đúng 0
Bình luận (0)
Nếu sinx + cosx 1/2 thì 3sinx + 2cosx bằng
Đọc tiếp
Nếu sinx + cosx= 1/2 thì 3sinx + 2cosx bằng
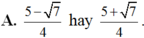
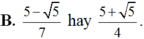
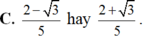
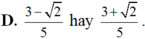
Chọn A.
Từ giả thiết ta suy ra: (sinx+ cosx) 2 = ¼
Suy ra: 2sinx.cosx = -3/4 hay sinx.cosx = -3/8
Khi đó sinx; cosx là nghiệm của phương trình
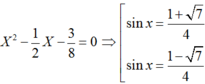
Do sinx + cosx = ½ nên 2(sinx + cosx) = 1
+) Với 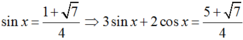
+) Với 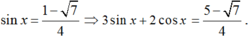
Đúng 0
Bình luận (0)
Nghiệm phương trình
cos
x
(
cos
x
)
+
3
sin
x
(
sin
x
+
2
)
sin
2
x
-
1...
Đọc tiếp
Nghiệm phương trình cos x ( cos x ) + 3 sin x ( sin x + 2 ) sin 2 x - 1 = 1
![]()
![]()
![]()
![]()
Tính các giới hạn
lim
x
→
π
3
2
sin
2
x
+
sin
x
-
1
2...
Đọc tiếp
Tính các giới hạn lim x → π 3 2 sin 2 x + sin x - 1 2 sin 2 x - 3 sin x + 1
lim x → π 3 2 sin 2 x + sin x - 1 2 sin 2 x - 3 sin x + 1 = 1 + 3 5 - 3 3
Đúng 0
Bình luận (0)
giải phương trình
1. sin2x+3sinx-cos2x=-2
2. sin2x+sinx-cos2x=0
`1)sin^2 x+3sin x-cos^2 x=-2`
`<=>sin^2 x+3sin x-1+sin^2 x+2=0`
`<=>2sin^2 x+3sin x+1=0`
`<=>[(sin x=-1),(sin x=-1/2):}`
`<=>[(x=-\pi/2 +k2\pi),(x=-\pi/6 +k2\pi),(x=[7\pi]/6+k2\pi):}` `(k in ZZ)`
`2)sin^2 x+sin x-cos^2 x=0`
`<=>sin^2 x+sin x-1+sin^2 x=0`
`<=>2sin^2 x+sin x-1=0`
`<=>[(sin x=-1),(sin x=1/2):}`
`<=>[(x=-\pi/2 +k2\pi),(x=\pi/6 +k2\pi),(x=[5\pi]/6 +k2\pi):}` `(k in ZZ)`
Đúng 2
Bình luận (0)
Nghiệm phương trình:
cosx
(
cosx
+
2
sinx
)
+
3
sinx
(
sinx
+
2
)
sin
2
x
-
1
1...
Đọc tiếp
Nghiệm phương trình: cosx ( cosx + 2 sinx ) + 3 sinx ( sinx + 2 ) sin 2 x - 1 = 1
A. x = ± π 4 + k2π, k ∈ Z
B. x = - π 4 + kπ, k ∈ Z
C. x = - π 4 + k2π, x = - 3 π 4 + k2π, k ∈ Z
D. x = - π 4 + k2π, k ∈ Z
Giải pt
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(sin2x-cos2x+3sinx-cosx-1=0\)
1.
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)
\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)
Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)
\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)
Đúng 0
Bình luận (0)
2.
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)
\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (0)
sin2x(tanx+1)=3sinx(cox-sinx)+3
Giải phương trình sau:
cosx
(
cosx
+
2
sinx
)
+
3
sinx
(
sinx
+
2
)
sin
2
x
-
1...
Đọc tiếp
Giải phương trình sau: cosx ( cosx + 2 sinx ) + 3 sinx ( sinx + 2 ) sin 2 x - 1 = 1
A. x = - π 4 + k2π
B. x = - 3 π 4 + k2π
C. x = ± π 4 + kπ
D. Cả A và B đúng