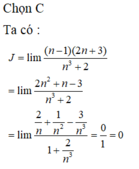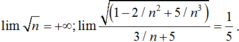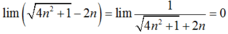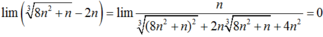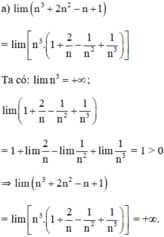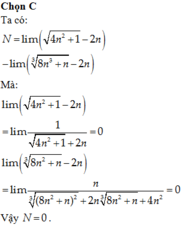Lim(12/n3+32/n3+...+(2n-1)2/n3)

Những câu hỏi liên quan
Tính giới hạn
J
l
i
m
(
n
-
1
)
(
2
n
+
3
n
)
n
3
+
2
? A. J 3 B. J 1 C. J 0 D. J 2
Đọc tiếp
Tính giới hạn J = l i m ( n - 1 ) ( 2 n + 3 n ) n 3 + 2 ?
A. J = 3
B. J = 1
C. J = 0
D. J = 2
Chọn kết quả đúng của
l
i
m
n
3
-
2
n
+
5
3
+
5
n
A. 5. B. 2/5. C. -∞. D. +∞.
Đọc tiếp
Chọn kết quả đúng của l i m n 3 - 2 n + 5 3 + 5 n
A. 5.
B. 2/5.
C. -∞.
D. +∞.
Giá trị của
D
l
i
m
(
n
2
+
2
n
-
n
3
+
2
n
2
3
)
bằng: A. +∞ B. -∞ C. 1/3 D. 1
Đọc tiếp
Giá trị của D = l i m ( n 2 + 2 n - n 3 + 2 n 2 3 ) bằng:
A. +∞
B. -∞
C. 1/3
D. 1
Tính giới hạn
L
l
i
m
n
3
-
2
n
3
n
2
+
n
-
2
. A. L
+
∞
B. L 0 C. L
1...
Đọc tiếp
Tính giới hạn L = l i m n 3 - 2 n 3 n 2 + n - 2 .
A. L = + ∞
B. L = 0
C. L = 1 3
D. L = - ∞
Tính các giới hạn sau: l i m ( − n 3 − 3 n 2 − 2 )
Giá trị của
N
l
i
m
(
4
n
2
+
1
-
8
n
3
+
n
3
)
bằng: A. +∞ B. -∞ C. 0 D. 1
Đọc tiếp
Giá trị của N = l i m ( 4 n 2 + 1 - 8 n 3 + n 3 ) bằng:
A. +∞
B. -∞
C. 0
D. 1
Tính các giới hạn sau: l i m n 3 + 2 n 2 - n + 1
Giá trị của. Nlim
4
n
2
+
1
-
8
n
3
+
n
3
bằng: A.
+
∞
. B.
-...
Đọc tiếp
Giá trị của.
N=lim 4 n 2 + 1 - 8 n 3 + n 3 bằng:
A. + ∞ .
B. - ∞ .
C. 0.
D. 1.
lim 3x3+2x2+x/n3+4
Sao biểu thức lại vừa x vừa n vậy bạn?
Ý bạn là: \(\lim\limits\dfrac{3n^3+2n^2+n}{n^3+4}\) ?
Đúng 0
Bình luận (0)
chứng minh n3+3n2+2n chia hết cho 6 (mình ko nhớ n3 hay n3)
Có: \(n^3+3n^2+2n=n^3+n^2+2n^2+2n\)
\(=n^2\left(n+1\right)+2n\left(n+1\right)=\left(2n+n^2\right)\left(n+1\right)\)
\(=n\left(n+2\right)\left(n+1\right)=n\left(n+1\right)\left(n+2\right)\)
Có \(n;n+1;n+2\)là 3 số nguyên liên tiếp
\(\Rightarrow\)trong đó có một số chia hết cho 3; có ít nhất một số chia hết cho 2
\(\Rightarrow\)\(n\left(n+1\right)\left(n+2\right)\)chia hết cho \(2\times3\)
\(\Rightarrow\)\(n\left(n+1\right)\left(n+2\right)\)chia hết cho 6
\(\Rightarrow\)\(n^3+3n^2+2n\)chia hết cho 6
Đúng 0
Bình luận (0)
Bạn Phạm Trần Minh Ngọc làm thiếu rồi, mình phải có thêm dữ kiện 2 và 3 là 2 số nguyên tố cùng nhau nữa mới đủ ~~
Đúng 0
Bình luận (0)
Có:
n^ 3 + 3n^ 2 + 2n
= n ^3 + n^ 2 + 2n ^2 + 2n
= n ^2( n + 1 )+ 2n (n + 1)
= (2n + n ^2 )(n + 1 )
= n( n + 2)( n + 1)
= n( n + 1)(n + 2)Có n;n + 1;n + 2là 3 số nguyên liên tiếp
⇒ trong đó có một số chia hết cho 3; có ít nhất một số chia hết cho 2
⇒n (n + 1)( n + 2) chia hết cho 2 × 3
⇒n (n + 1)( n + 2) chia hết cho 6
⇒n^ 3 + 3n^ 2 + 2n chia hết cho 6
Đúng 0
Bình luận (0)