Cho tam giác abc nhọn AH vuông BC (H thuộc BC). Biết AC=20cm,AH=12cm,BH=5cm
A) tính chu vi tam giác abc
B) tính diện tích tam giác abc
cho tam giác ABC nhọn đường cao AH (H thuộc BC)tính chu vi tam giác ABC,biết AC=20cm, AH=12cm và BH=5cm
\(HC=\sqrt{AC^2-AH^2}=16\left(cm\right)\)
BC=BH+HC=21(cm)
\(AB=\sqrt{AH^2+HB^2}=13\left(cm\right)\)
C=AB+BC+AC=13+20+21=54(cm)
Xét tam giác vuông AHB có
AH ^2 + BH ^2 = AB ^2 ( Pytago)
=> AB ^2 = 12^2 + 5^2
=> Ab = 13
Xét tam giác vuông AHC có
AH^2 + HC^2 = AC ^2 ( Pytago)
=> HC^2 = AC^2 - AH^2 = 20^2 -12^2
=> HC =16
BC = HC + BH = 16 + 5 = 21
Chu vi tam giác ABC là AB + AC + BC = 13 + 20 + 21= 54 cm
cho tam giác ABC nhọn, AH vuông BC biết AC=20cm ; AH=12cm ; BH=5cm. Tính chu vi tam giác ABC
\(AB^2=AH^2+BH^2\)
\(AB=12^2+5^2=169\)
\(AB=\sqrt{169}=13\left(cm\right)\)
▲AHC vuông tại H ta có:
HC\(^2\)=\(AC^2-AH^2\)=\(20^2-12^2\)=256
\(\)Chu vi ▲ABC là:
AB+BC+AC=AB+BH+HC+AC=\(13+5+16+20=54\left(cm\right)\)
Tham khảo:
Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = 122 + HC2
=> HC2 = 202 - 122
HC2 = 400 - 144 = 256 = 162
=> HC = 16 cm
Ta có : BC = HC + HB = 16 + 5 = 21 cm
Tam giác ABH vuông tại H nên :
AB2 = AH2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169 = 132
=> AB = 13 cm
Vậy chu vi tam giác ABC là :
AB + AC + BC = 13 + 20 + 21 = 54 (cm)
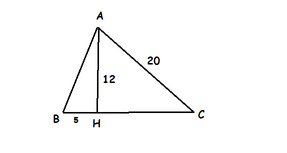
Ta có : \(\Delta ABH\) vuông tại H
Theo đl pytago ta có : \(AH^2+BH^2=AB^2\)
-> \(AB=\sqrt{12^2+5^2}=13\left(cm\right)\)
\(\Delta ACH\) vuông tại H
Theo đl pytago ta có : \(AC^2-AH^2=CH^2\)
-. \(CH=\sqrt{20^2-12^2}=16\left(cm\right)\)
Chu vi \(\Delta ABC=AB+AC+BC=13+20+16+5=54\left(cm\right)\)
cho tam giác nhọn abc kẻ ah vuông góc với bc biết ac=20cm ah=12cm bh=16cm tính chu vi tam giác abc
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=12^2+16^2=400\)
hay AB=20(cm)
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow HC^2=AC^2-AH^2=20^2-12^2=256\)
hay HC=16(cm)
Ta có: BH+HC=BC(H nằm giữa B và C)
nên BC=16+16=32(cm)
Chu vi của tam giác ABC là:
\(C_{ABC}=AB+BC+AC=20+32+20=72\left(cm\right)\)
Lời giải:
Áp dụng định lý Pitago cho tam giác $AHC$ vuông tại $H$:
$HC=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm)
Áp dụng định lý Pitago cho tam giác $AHB$ vuông tại $H$:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20$ (cm)
Chu vi tam giác $ABC$:
$AB+BC+AC=AB+BH+CH+AC=20+16+16+20=72$ (cm)
Giúp mình với !!! vẽ hình giúp mình với nha !! ![]()
Bài 1: Cho tam giác ABC vuông tại A. Biết BC = 41cm; AC = 40cm. Tính
a) Độ dài cạnh AB
b) Chu vi tam giác ABC
Bài 2: Cho tam giác ABC nhọn. Kẻ AH vuông góc với BC. Biết AC = 20cm; AH =
12cm; HB = 5cm
a) Tính độ dài cạnh AB
b) Tính chu vi tam giác ABC
Bài 3: Cho tam giác ABC có BC = 10cm , AB = 6cm và AC = 8cm . Tam giác ABC là
tam giác gì ? Vì sao ?
Bài 4: Cho tam giác ABC vuông tại A, có B 60 0 và AB = 5cm. Tia phân giác của góc
B cắt AC tại D. Kẻ DE vuông góc với BC (EBC) . Chứng minh:
a) ABD = EBD.
b) ABE là tam giác đều.
c) AEC cân.
d) Tính độ dài cạnh AC.
Bài 5: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC ( HBC )
a) Chứng minh: AHB = AHC
b) Giả sử AB = AC = 5cm, BC = 8cm. Tính độ dài AH
c) Trên tia đối của tia HA lấy điểm M sao cho HM = HA. Chứng minh ABM
cân
d) Chứng minh BM // AC
Bài 6: Cho tam giác ABC vuông tại A, phân giác BE. Kẻ EK vuông góc với BC tại K.
Gọi M là giao điểm của BA và KE. Chứng minh :
a) ΔABE = ΔKBE
b) EM = EC
c) AK // MC
d) So sánh AE và EC
e) Gọi N là trung điểm của MC. Chứng minh 3 điểm B, E, N thẳng hàng
Bài 7: Cho ABC có AB = AC =10cm, BC = 12cm. Vẽ AH vuông góc BC tại H.
a) Chứng minh: ABC cân.
b) Chứng minh AHB AHC, từ đó chứng minh AH là tia phân giác của góc
A.
c) Từ H vẽ HM AB ( ) M AB và kẻ HN AC ( ) N AC . C/m: BHM = HCN
d) Tính độ dài AH.
e) Từ B kẻ Bx AB, từ C kẻ Cy AC chúng cắt nhau tại O. Tam giác OBC là
tam giác gì? Vì sao?
bạn đăng tách ra nhé
Bài 1 :
Theo định lí Pytago tam giác ABC vuông tại A
\(AB=\sqrt{BC^2-AC^2}=9cm\)
Chu vi tam giác ABC là 41 + 40 + 9 = 90 cm
Cho tam giác ABC nhọn .kẻ AH vuông góc với BC .Tính chu vi tam giác ABC biết AC=20cm,AH=12cm,BH=5cm
Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = 122 + HC2
=> HC2 = 202 - 122
HC2 = 400 - 144 = 256 = 162
=> HC = 16 cm
Ta có : BC = HC + HB = 16 + 5 = 21 cm
Tam giác ABH vuông tại H nên :
AB2 = AH2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169 = 132
=> AB = 13 cm
Vậy chu vi tam giác ABC là :
AB + AC + BC = 13 + 20 + 21 = 54 (cm)
chu vi là 54 cm
\(\Delta ABH\)vuông tại H \(\Rightarrow AH^2+BH^2=AB^2\)( định lý Pytago )
mà \(AH=12cm\), \(BH=5cm\)
\(\Rightarrow12^2+5^2=AB^2\)\(\Rightarrow AB^2=144+25\)
\(\Rightarrow AB^2=169\)\(\Rightarrow AB=13\)( cm )
\(\Delta AHC\)vuông tại H \(\Rightarrow AH^2+HC^2=AC^2\)( định lý Pytago )
\(\Rightarrow HC^2=AC^2-AH^2\)
mà \(AC=20cm\); \(AH=12cm\)
\(\Rightarrow HC^2=20^2-12^2\)\(\Rightarrow HC^2=400-144\)
\(\Rightarrow HC^2=256\)\(\Rightarrow HC=16\)( cm )
mà \(BC=HB+HC\)\(\Rightarrow BC=5+16=21\)( cm )
\(\Rightarrow P_{ABC}=AB+AC+BC=13+20+21=54\)( cm )
Vậy chu vi của \(\Delta ABC\)là 54 cm
cho tam giác nhọn ABC kẻ AH vuông góc với BC . tính chu vi của tam giác ABC biết AC=20cm AH=12cm BH=5cm
cho tam giác nhọn ABC . Kẻ AH vuông góc vớiBC tại H , biết AB = 13 cm AH=12cm , CH = 5cm
a) ghi giả thiết và kết luận
b) Tính BH , AC,BC?
c) tính cho vi hình tam giác
b: \(BH=\sqrt{AB^2-AH^2}=5\left(cm\right)\)
BC=BH+CH=5+5=10(cm)
\(AC=\sqrt{12^2+5^2}=13\left(cm\right)\)
b: C=AB+BC+AC=10+13+13=36(cm)
bài 1 :tam giác ABC có AD=20cm dựng AH vuông góc vs BC tại H,AH =12cm BH=5cm . hãy tính chu vi tam giác ABC
bài 2 :
tam giác ABC có AC=20cm dựng AH vuông góc vs BC tại H,HC=16cm BH=9cm . hãy tính chu vi tam giác ABC
tam giác AHB vuông tại H ,THEO ĐỊNH LÝ PYTA GO TA CÓ
AB^2=AH^2+BH^2=>AB^2=169=>AB=13 CM
TAM GIÁC AHC VUÔNG TẠI H,THEO ĐỊNH LÝ PYTA GO TA CÓ
HC^2+AH^2=AC^2=>HC^2=AC^2-AH^2=>HC^2=256=>HC=16CM
VÌ H NẰM GIỮA BC => BC=BH+HC=21 CM
=>CHU VI TAM GIÁC ABC LÀ
AB+AC+BC=13+21+20=54 CM
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AC= 20cm, AH = 12 cm và BH = 5cm
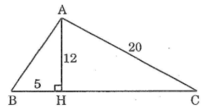
∆AHB có ∠(AHB) =90°
Theo định lý pitago, ta có:
AB2=AH2+HB2
= 122+52=169
Vậy AB = 13 cm
∆AHC có ∠(AHC) =90o
Theo định lý pitago, ta có:
AC2=AH2+HC2
HC2=AC2-AH2=202-122=400-144=256
Vậy HC = 16cm
Ta có: BC = BH + HC = 5 +16 = 21cm
Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm