a: Xét tứ giác OBAC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)

nên OBAC là tứ giác nội tiếp

=>O,B,A,C cùng thuộc một đường tròn

Xét (O) có

AB,AC là tiếp tuyến

Do đó: AB=AC

=>A nằm trên đường trung trực của BC(1)

OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra OA là đường trung trực của BC

=>OA\(\perp\)BC (3)

b: Xét (O) có

ΔBCD nội tiếp

CD là đường kính

Do đó: ΔDBC vuông tại B

=>DB\(\perp\)BC(4)

Từ (3) và (4) suy ra DB//OA

c: Đề sai rồi bạn

a: Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\)

nên ABOC là tứ giác nội tiếp

=>A,B,O,C cùng thuộc một đường tròn

b: Xét (O) có

AB,AC là các tiếp tuyến

Do đó: AB=AC

=>A nằm trên đường trung trực của BC(1)

Ta có: OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra AO là đường trung trực của BC

=>AO\(\perp\)BC tại trung điểm H của BC

Gọi K là giao điểm của OS và ED

Xét (O) có

SE,SD là các tiếp tuyến

Do đó: SE=SD

=>S nằm trên đường trung trực của ED(3)

Ta có: OE=OD

=>O nằm trên đường trung trực của ED(4)

Từ (3) và (4) suy ra SO là đường trung trực của ED

=>SO\(\perp\)ED tại trung điểm K của ED

Xét ΔOBA vuông tại B có BH là đường cao

nên \(OH\cdot OA=OB^2=R^2\left(5\right)\)

Xét ΔODS vuông tại D có DK là đường cao

nên \(OK\cdot OS=OD^2=R^2\left(6\right)\)

Từ (5) và (6) suy ra \(OH\cdot OA=OK\cdot OS\)

=>\(\dfrac{OH}{OK}=\dfrac{OS}{OA}\)

Xét ΔOHS và ΔOKA có

\(\dfrac{OH}{OK}=\dfrac{OS}{OA}\)

góc HOS chung

Do đó: ΔOHS đồng dạng với ΔOKA

=>\(\widehat{OHS}=\widehat{OKA}\)

=>\(\widehat{OHS}=90^0\)

=>HO\(\perp\)SH tại H

mà HO\(\perp\)BH tại H

và SH,BH có điểm chung là H

nên S,H,B thẳng hàng

mà H,B,C thẳng hàng

nên S,B,H,C thẳng hàng

=>S,B,C thẳng hàng

a: góc ABO+góc ACO=90+90=180 độ

=>ABOC nội tiếp

b: Xét ΔABM và ΔANB có

góc ABM=góc ANB

góc BAM chung

=>ΔABM đồng dạng với ΔANB

=>AB/AN=AM/AB

=>AB^2=AN*AM

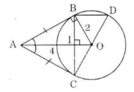
 Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.

Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)

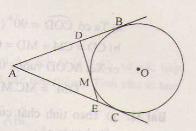
Chứng minh AB=AC; DB=DM và EC=EM.

Chu vi

= AD + DM + ME + AE

= AD + DB + EC + AE

= AB + AC

 = 2AB.

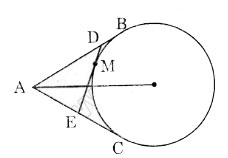
Ta có AB = AC; DB = DM;
EC = EM.
Chu vi Δ ADE:
AD +AE +DE = AD +DM + AE + EM
=AD + DB + AE + EC = AB + AC = 2AB

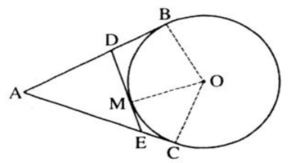
Theo tính chất hai tiếp tuyến cắt nhau ta có:

    DM = DB, EM = EC, AB = AC

Chu vi ΔADE:

    CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)