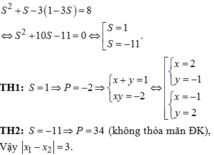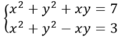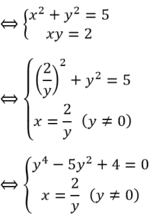Tập nghiệm của hệ phương trình x+xy+y=2,x2+y2+xy=4 là

Những câu hỏi liên quan
Gọi
x
1
;
y
1
,
x
2
;
y
2
là hai nghiệm phân biệt của hệ phương trình ...
Đọc tiếp
Gọi x 1 ; y 1 , x 2 ; y 2 là hai nghiệm phân biệt của hệ phương trình x 2 + y 2 - x y + x + y = 8 x y + 3 x + y = 1 . Tính x 1 - x 2 .
A.3
B.2
C.1
D.0
Tập nghiệm của hệ phương trình
x
+
y
+
x
y
-
13
x
2
+
y
2...
Đọc tiếp
Tập nghiệm của hệ phương trình x + y + x y = - 13 x 2 + y 2 - x - y = 32 là:
A. - 5 ; 2 ; 5 ; - 3
B. - 5 ; 2 ; 5 ; - 3 ; - 3 ; 5
C. - 5 ; 2 ; - 2 ; 5 ; 5 ; - 3 ; - 3 ; 5
D. - 5 ; 2 ; 2 ; - 5 ; 5 ; - 3 ; - 3 ; 5
t 2
Ta có: x + y + x y = - 13 x 2 + y 2 - x - y = 32 ⇔ x + y + x y = - 13 ( x + y ) 2 - 2 x y - ( x + y ) = 32
Đặt S = x+ y; P = xy . Khi đó, hệ phương trình trên trở thành:
S + P = - 13 ( 1 ) S 2 - 2 P - S = 32 ( 2 )
Từ (1) suy ra: P = -S – 13 thay vào (2) ta được:
S 2 – 2(-S – 13) – S = 32
⇔ S 2 + 2 S + 26 - S - 32 = 0 ⇔ S 2 + S - 6 = 0 ⇔ [ S = 2 S = - 3
* Với S = 2 thì P = -15 . Khi đó , x và y là nghiệm phương trình:
t 2 - 2t – 15 = 0 ⇔ [ t = 5 t = - 3
* Với S = -3 thì P = -10. Khi đó, x và y là nghiệm phương trình:
t 2 + 3t – 10 =0 ⇔ [ t = 2 t = - 5
Vậy hệ phương trình đã cho có 4 nghiệm ( 5; -3); (-3; 5); (2; -5); (-5; 2).
Chọn D.
Đúng 0
Bình luận (0)
Hệ phương trình
x
2
+
y
2
4
x
+
y
2
có nghiệm là (x; y) với x y. Khi đó xy bằng: A. 0...
Đọc tiếp
Hệ phương trình x 2 + y 2 = 4 x + y = 2 có nghiệm là (x; y) với x > y. Khi đó xy bằng:
A. 0
B. 1
C. 2
D. 4
Nếu
x
;
y
là nghiệm của hệ phương trình:
x
2
−
4
x
y
+
y
2...
Đọc tiếp
Nếu x ; y là nghiệm của hệ phương trình: x 2 − 4 x y + y 2 = 1 y − 4 x y = 2 thì xy bằng:
A. 4
B. -4
C. 1
D. Không tồn tại giá trị của xy
Trừ vế cho vế phương trình (1) cho (2) ta được:
x 2 + y 2 − y = − 1 ⇔ x 2 + y 2 − y + 1 = 0
Ta có:
x 2 ≥ 0 , ∀ x y 2 − y + 1 = y − 1 2 2 + 3 4 > 0 , ∀ y ⇒ x 2 + y 2 − y + 1 > 0 , ∀ x , y
Do đó phương trình x 2 + y 2 − y + 1 = 0 vô nghiệm
Vậy không tồn tại giá trị của xy
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Hệ phương trình
x
2
+
y
2
4
x
+
y
2
có nghiệm là (x; y) với x y. Khi đó tích xy bằng: A. 0 B. 1 C. 2 D. 4
Đọc tiếp
Hệ phương trình x 2 + y 2 = 4 x + y = 2 có nghiệm là (x; y) với x > y. Khi đó tích xy bằng:
A. 0
B. 1
C. 2
D. 4
Đáp án A
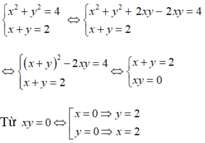
Vậy hệ phương trình có hai nghiệm (x; y) = (0; 2); (x; y) = (2; 0) Từ giả thiết x > y nên x = 2; y = 0 ⇒ xy = 0
Đúng 0
Bình luận (0)
Số nghiệm của hệ phương trình
x
2
+
y
2
+
x
y
7...
Đọc tiếp
Số nghiệm của hệ phương trình x 2 + y 2 + x y = 7 x 2 + y 2 - x y = 3 là:
A. 2
B. 1
C. 3
D. 4
Biết rằng hệ phương trình:
x
2
+
y
2
+
2
x
y
8
2...
Đọc tiếp
Biết rằng hệ phương trình: x 2 + y 2 + 2 x y = 8 2 x + y = 4 có nghiệm duy nhất (x; y). Tính x y
A. 3
B. 1 2
C. 2
D. 1
Điều kiện: xy > 0
2 x 2 + y 2 + 2 x y = 16 x + y + 2 x y = 16 ⇔ 2 x 2 + y 2 = x + y ⇔ ( x – y ) 2 = 0 ⇔ x = y
Thay x = y vào x + y + x y = 16 ta được
2x + 2|x| = 16 ⇔ x + |x| = 8 ⇒ x = 4 ⇒ y = x = 4
Vậy hệ có một cặp nghiệm duy nhất (x; y) = (4; 4)
Khi đó x y = 4 4 = 1
Đáp án:D
Đúng 0
Bình luận (0)
Tập nghiệm của pt: x4-8x ²-90Hệ pt: x2+y2+xy7 x2+y2-xy3có nghiệm là.Cho phương trình(x2-3x+3)2-2x2+6x-50 Nếu đặt tx2-3x+3thì phương trình đã cho trở thành phương trình nào Gọi là tập tất cả các giá trị nguyên của tham số thuộc đoạn −2;6 để phương trình x2+4mx +m2có hai nghiệm dương phân biệt. Tổng các phần tử trong S bằngA. -3.B. 2.C. 18.D. 21.
Đọc tiếp
Tập nghiệm của pt: x4-8x ²-9=0
Hệ pt: x2+y2+xy=7
x2+y2-xy=3
có nghiệm là.
Cho phương trình(x2-3x+3)2-2x2+6x-5=0 Nếu đặt t=x2-3x+3
thì phương trình đã cho trở thành phương trình nào
Gọi là tập tất cả các giá trị nguyên của tham số thuộc đoạn −2;6 để phương trình x2+4mx +m2
có hai nghiệm dương phân biệt. Tổng các phần tử trong S bằng
A. -3.
B. 2.
C. 18.
D. 21.
Cho (x,y) với x,y nguyên là nghiệm của hệ phương trình
x
y
+
y
2
+
x
7
y
(
1
)...
Đọc tiếp
Cho (x,y) với x,y nguyên là nghiệm của hệ phương trình x y + y 2 + x = 7 y ( 1 ) x 2 y + x = 12 ( 2 ) thì tích xy bằng:
A. 1
B. 2
C. 3
D. 4
Điều kiện y ≠ 0
Hệ phương trình tương đương với x + y + x y = 7 ( 1 ) x x y + 1 = 12 ( 2 )
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12

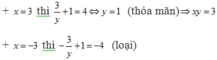

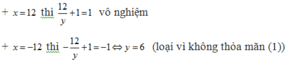
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Cho hệ phương trình:
2
x
2
+
x
y
−
y
2
0
x
2
−...
Đọc tiếp
Cho hệ phương trình: 2 x 2 + x y − y 2 = 0 x 2 − x y − y 2 + 3 x + 7 y + 3 = 0 . Các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là:
A. (2; −2), (3; −3).
B. (−2; 2), (−3; 3).
C. (1; −1), (3; −3).
D. (−1; 1), (−4; 4).
Phương trình 1 ⇔ x + y 2 x - y = 0 ⇔ x = − y 2 x = y
Trường hợp 1: x = - y thay vào (2) ta được x 2 - 4 x + 3 = 0 ⇔ x = 1 x = 3
Suy ra hệ phương trình có hai nghiệm là (1; −1), (3; −3).
Trường hợp 2: 2 x = y thay vào (2) ta được - 5 x 2 + 17 x + 3 = 0 phương trình này không có nghiệm nguyên.
Vậy các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là (1; −1) và (3; −3).
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)