Cho tứ giác ABCD có bốn đỉnh thuộc đường tròn. Gọi M,N,P,Q lần lượt là điểm chính giữa các cung AB,BC,CD,DA. Chứng minh:MP vuông góc với NQ.

Những câu hỏi liên quan
cho tứ giác ABCD có hai cạnh đối AD và BC bằng nhau.Gọi M,N,P,Q lần lượt là trung điểm của AB,AC,CD,BD.
a)Chứng minh:MQ=NP=MN
b)Chứng minh:MP vuông góc với NQ
cho tứ giác ABCD có hai cạnh đối AD và BC bằng nhau.Gọi M,N,P,Q lần lượt là trung điểm của AB,AC,CD,BD.
a)Chứng minh:MQ=NP=MN
b)Chứng minh:MP vuông góc với NQ
\(a,\) Chứng minh đc \(MQ,NP,MN\) lần lượt là đường trung bình \(\Delta ABD,\Delta ADC,\Delta ABC\)
\(\Rightarrow MQ=\dfrac{1}{2}AD;NP=\dfrac{1}{2}AD;MN=\dfrac{1}{2}BC\\\Rightarrow MQ=NP=MN\left(\dfrac{1}{2}AC=\dfrac{1}{2}BC\right)\)
\(b,\) Chứng minh thêm đc \(PQ\) là đtb \(\Delta BDC\)
\(\Rightarrow PQ=\dfrac{1}{2}BC\Rightarrow MQ=QP=PN=NM\left(\dfrac{1}{2}BC=\dfrac{1}{2}AD\right)\)
\(\Rightarrow MNPQ\) là hình thoi
\(\Rightarrow MP\perp NQ\)
Đúng 3
Bình luận (0)
Cho tứ giác ABCD nội tiếp đường tròn đồng thời lại ngoại tiếp một đường tròn khác có các tiếp điểm M,N,P,Q lần lượt với các cạnh AB , BC , CD , DA của tứ giác đã cho . Chứng minh rằng MP vuông góc với NQ
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh M, N, P, Q cùng nằm trên một đường tròn
Ta có MNPQ là hình chữ nhật tâm O => M,N,P,Q cùng thuộc (O;OM)
Đúng 0
Bình luận (0)
cho tứ giác ABCD có 2 đường chéo vuông góc với nhau. Gọi M,N,P,Q lần lượt là trung điểm của AB,BC,CD,DA. Chứng minh 4 điểm trên cùng nằm trên một đường tròn
Trên đường tròn (O) cho các điểm A, B, C, D theo thứ tự đó. Gọi M, N, P, Q lần lượt là điểm chính giữa của các cung AB, BC, CD và DA. Chứng minh các đường thẳng MQ và NP vuông góc với nhau.
có sđ MN + sđ PQ = 1/2 sđ AB + 1/2 sđ BC + 1/2 sđ CD + 1/2 sđ AD = 180 độ
mà MIN = 1/2 ( sđ MN + sđ PQ )
nên MIN = 90 độ => MI vuông góc NI hay MP vuông góc với NQ
Có sđ MN +sđPQ=1/2sđAB+1/2sđBC +1/2sđCD+1/2sđAD=180độ
mà MIN =1/2(sđMN+sđPQ)
Nên MIN=90độ =>MI vuông góc MI
Hay MQ vuông góc NP
Xem thêm câu trả lời
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi E, F, G, H lân lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh bốn điểm E, F, G, H cùng thuộc một đường tròn.
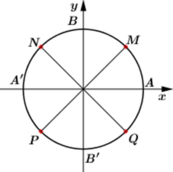
Trên đường tròn đơn vị, gọi các điểm A, B, A’, B’ lần lượt là các điểm (1;0), (0;1), (-1;0), (0;-1). Cho M, N, P, Q lần lượt là các điểm chính giữa các cung AB, BC, CD, DA. Cung có đầu mút là A và mút cuối trùng với một trong bốn điểm M, N, P, Q. Số do của là A. α 300+ k.3600 B. α 600+ k.3600
Đọc tiếp
Trên đường tròn đơn vị, gọi các điểm A, B, A’, B’ lần lượt là các điểm (1;0), (0;1), (-1;0), (0;-1). Cho M, N, P, Q lần lượt là các điểm chính giữa các cung AB, BC, CD, DA. Cung có đầu mút là A và mút cuối trùng với một trong bốn điểm M, N, P, Q. Số do của là
A. α = 300+ k.3600
B. α= 600+ k.3600
![]()
![]()
Chọn D.
+ Ta có số đo cung ![]()
+ Ta có ![]()
+ Để mút cuối cùng trùng với một trong bốn điểm M; N; P; Q thì chu kì của cung α là ![]()
Vậy số đo cung ![]()
Đúng 0
Bình luận (0)
Bài 1 : Cho hình vuông ABCD có cạnh bằng 3 cm . Chứng minh rằng : 4 đỉnh của hình vuông ABCD cùng nằm trên 1 đường tròn . Hãy tính bán kính đường tròn đó Bài 2 : Cho tam giác nhọn ABC . Vẽ đường tròn tâm O , bán kính BC , nó cắt các cạnh AB, AC theo thứ tự ở D và E a)CMR: CD vuông góc với AB , BE vuông góc với AC b) gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BCBài 3:Cho hình thang ABCD , AB//CD, ABCD , có góc Cgóc D60 độ , CD2AD . Chứng minh 4 điểm A, B, C, D cùng thuộc 1 đường trò...
Đọc tiếp
Bài 1 : Cho hình vuông ABCD có cạnh bằng 3 cm . Chứng minh rằng : 4 đỉnh của hình vuông ABCD cùng nằm trên 1 đường tròn . Hãy tính bán kính đường tròn đó
Bài 2 : Cho tam giác nhọn ABC . Vẽ đường tròn tâm O , bán kính BC , nó cắt các cạnh AB, AC theo thứ tự ở D và E
a)CMR: CD vuông góc với AB , BE vuông góc với AC
b) gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BC
Bài 3:Cho hình thang ABCD , AB//CD, AB<CD , có góc C=góc D=60 độ , CD=2AD . Chứng minh 4 điểm A, B, C, D cùng thuộc 1 đường tròn. Tính diện tích đường tròn đó biết CD=4cm
Bài 4:Cho tam giác ABC vuông tại A. Trên AB, AC lần lượt lấy các điểm D, E . Gọi M, N, P, Q lần lượt là trung điểm của DE , EB, BC, CD. Chứng minh 4 điểm M, N, P, Q cùng thuộc 1 đường tròn
@ Trần Ngọc Huyền @ Em lần sau nhớ chia bài ra đăng nhiều lần nhé! .
Đúng 0
Bình luận (0)
Đồng ý với cô Nguyễn Thị Linh Chi
Đăng nhiều thế mới nhìn đã choáng



















