Cho tam giác ABC cân tại A. Nội tiếp đường trong (O). Từ B kẻ đường thẳng vuông góc với OC. Đường thẳng này cắt AC tại D và cắt (O) tại E ( E khác B). Cho biết AB = 8cm và BC =4cm, tính đọ dài các đoạn thẳng DE, OA, OD.
giúp vsssss
Những câu hỏi liên quan
Cho đường tròn (O). Các đường cao BE và CF của tam giác ABC cắt nhau tại H và cắt (O) lần lượt tại E' và F' (E' khác B và F' khác C).
a, Chứng minh tứ giác BCEF nội tiếp
b, Chứng minh EF//E'F'
c, Kẻ OI vuông góc với BC( I thuộc BC). Đường thẳng vuông góc với HI tại H cắt đường thẳng AB tại M và cắt đường thẳng AC tại N. Chứng minh tam giác IMN cân
Tam giác ở trong hay ngoài hình tròn?
Cho tam giác ABC, không có góc tù (AB<AC) nội tiếp đường tròn (O;R). B,C cố định, A di động trên cung lớn BC . Các tiếp tuyến tại B,C cắt nhau tại M. Từ M kẻ đường thẳng song song với AB, đường thẳng này cắt (O) tại D và E (D thuộc cung nhỏ BC ), cắt BC tại F, cắt AC tại K.
a) CMR:tứ giác MBOC nội tiếp
b) CMR: FK.FM=FD.FE
GIÚP MÌNH VỚI, MÌNH ĐANG CẦN GẤP !!
a)Xét tứ giác MBOC có
\(\widehat{OBM}\) và \(\widehat{OCM}\) là hai góc đối
\(\widehat{OBM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MBOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn (AB AC), nội tiếp đường tròn (O; R). Các tiếp tuyến tại B và C cắt nhau tại M. Gọi H là giao điểm của OM và BC. Từ M kẻ đường thẳng song song với AC, đường thẳng này cắt (O) tại E và F (E thuộc cung nhỏ BC), cắt BC tại I, cắt AB tại Ka) Chứng minh: MO vuông góc BC và ME.MF MH.MOb) Chứng minh rằng tứ giác MBKC là tứ giác nội tiếp. Từ đó suy ra 5 điểm M, B, K, O, C cùng thuộc một đường trònc) Đường thẳng OK cắt O tại N và P (N thuộc cung nhỏ AC). Đường thẳng PI cắt O tại Q...
Đọc tiếp
Cho tam giác ABC nhọn (AB > AC), nội tiếp đường tròn (O; R). Các tiếp tuyến tại B và C cắt nhau tại M. Gọi H là giao điểm của OM và BC. Từ M kẻ đường thẳng song song với AC, đường thẳng này cắt (O) tại E và F (E thuộc cung nhỏ BC), cắt BC tại I, cắt AB tại K
a) Chứng minh: MO vuông góc BC và ME.MF = MH.MO
b) Chứng minh rằng tứ giác MBKC là tứ giác nội tiếp. Từ đó suy ra 5 điểm M, B, K, O, C cùng thuộc một đường tròn
c) Đường thẳng OK cắt O tại N và P (N thuộc cung nhỏ AC). Đường thẳng PI cắt O tại Q (Q khác P). Chứng minh ba điểm M, N, Q thẳng hàng
cho tam giác ABC nhọn nội tiếp đường tròn (O), 2 đường cao BE, CF cắt nhau tại H và cắt đường tròn tại E' và F'.
a) BECD là tứ giác nội tiếp
b) EF// E'F'
c) kẻ OI vuông góc với BC, đường thẳng vuông góc với HI tại H cắt đường thẳng AB tại m và cắt đường thẳng AC tại N. cmr tam giác IMN cân
1. Cho tam giác ABC không có góc tù (AB AC), nội tiếp đường tròn (O; R). (B, C cố định, A di động trên cung lớn BC). Các tiếp tuyến tại B và C cắt nhau tại M. Từ M kẻ đường thẳng song song với AB, đường thẳng này cắt (O) tại D và E (D thuộc cung nhỏ BC), cắt BC tại F, cắt AC tại I.a) Chứng minh rằng góc MBC góc BAC . Từ đó suy ra MBIC là tứ giác nội tiếp.b) Chứng minh rằng: FI.FM FD.FE.c) Đường thẳng OI cắt (O) tại P và Q (P thuộc cung nhỏ AB). Đường thẳng QF cắt (O) tại T (T khác Q). Chứng m...
Đọc tiếp
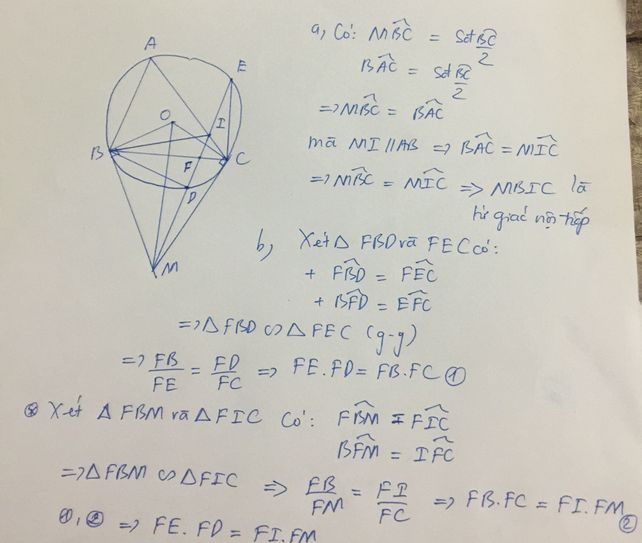
1. Cho tam giác ABC không có góc tù (AB < AC), nội tiếp đường tròn (O; R). (B, C cố định, A di động trên cung lớn BC). Các tiếp tuyến tại B và C cắt nhau tại M. Từ M kẻ đường thẳng song song với AB, đường thẳng này cắt (O) tại D và E (D thuộc cung nhỏ BC), cắt BC tại F, cắt AC tại I.
a) Chứng minh rằng góc MBC = góc BAC . Từ đó suy ra MBIC là tứ giác nội tiếp.
b) Chứng minh rằng: FI.FM = FD.FE.
c) Đường thẳng OI cắt (O) tại P và Q (P thuộc cung nhỏ AB). Đường thẳng QF cắt (O) tại T (T khác Q). Chứng minh ba điểm P, T, M thẳng hàng.
đây nha bn
tk cho mk nha
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O) (AB AC), đường cao BE của tam giác kéo dài cắt đường tròn (O) tại K. Kẻ KD vuông góc với BC tại D.a) Chứng minh tứ giác KEDC nội tiếp. Xác định tâm của đường tròn này.b) Chứng minh KB là tia phân giác của góc AKD.c) Tia DE cắt đường thẳng AB tại I. Qua E kẻ đường thẳng vuông góc với OA, đường thẳng này cắt AB tại H. Chứng minh CH // KI.Các bạn giúp mình phần c nha 3
Đọc tiếp
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O) (AB <AC), đường cao BE của tam giác kéo dài cắt đường tròn (O) tại K. Kẻ KD vuông góc với BC tại D.
a) Chứng minh tứ giác KEDC nội tiếp. Xác định tâm của đường tròn này.
b) Chứng minh KB là tia phân giác của góc AKD.
c) Tia DE cắt đường thẳng AB tại I. Qua E kẻ đường thẳng vuông góc với OA, đường thẳng này cắt AB tại H. Chứng minh CH // KI.
Các bạn giúp mình phần c nha <3
Cho tam giác ABC vuông tại A (AB < AC) nội tiếp trong đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng: Tam giác HAF cân
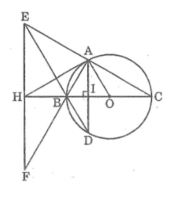
Tam giác EBF cân tại B nên HE = HF
Tam giác AEF vuông tại A có AH là đường trung tuyến ứng với cạnh huyền nên: HA = HE = HF = (1/2).EF (tính chất tam giác vuông)
Vậy tam giác AHF cân tại H.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC) nội tiếp trong đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng: Tam giác EBF cân
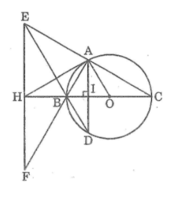
Gọi I là giao điểm của AD và BC
Vì BC là đường trung trực của AD nên theo tính chất đường trung trực ta có:
BA = BD
Tam giác BAD cân tại B có BI ⊥ AD nên BI là tia phân giác của góc ABD
Tam giác EBF có BH là tia phân giác của góc EBF và BH ⊥ EF nên tam giác EBF cân tại B.
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a(ab<ac) nội tiếp (o;r) đường kính bc. Kẻ dây ad vuông góc với bc. gọi e là giao điểm của db và ca. qua e kẻ đường thẳng vuống góc với bc cắt bc tại h, cắt ab tại f. chứng minh rằng:
a) tam giác ebf cân
b) tam giác haf cân
c) ha là tiếp tuyến của (o)