Tìm x thuộc Z. Thỏa mãn: x . (x - 3) < 0

Những câu hỏi liên quan
1.Tìm x;y thuộc N : x^3 -7=y^2
2.Tìm p;q thuộc P và x thuộc z thỏa mãn: x^5+px+3q=0
3, Tìm x;y thuộc Z thỏa mãn 6x^3-xy(11x+3y)+2y^3=6
tìm x,y thuộc Z thỏa mãn x^3+3xy+2y-5=0
Tìm x,y,z thuộc N* thỏa mãn hệ: x+y-z=0 và x3+y3-z2=0.
a) Tìm ĐKXĐ và rút gọn M
b) Tìm x thuộc Z để M thuộc Z. Tìm giá trị nguyên đó
c) Tìm x thỏa mãn M<0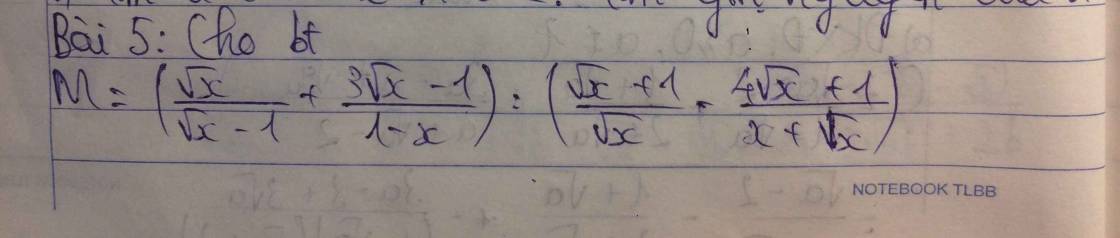
a:
ĐKXĐ: x>0; x<>1\(M=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{\left(\sqrt{x}+1\right)^2-4\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x+2\sqrt{x}+1-4\sqrt{x}-1}\)
\(=\dfrac{x+\sqrt{x}-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}}{x-2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
b: M là số nguyên
=>\(\sqrt{x}-1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2+1⋮\sqrt{x}-2\)
=>căn x-2 thuộc {1;-1}
=>căn x thuộc {3;1}
=>x thuộc {9;1}
Kết hợp ĐKXĐ, ta được: x=9
c: M<0
=>\(\dfrac{\sqrt{x}-1}{\sqrt{x}-2}< 0\)
=>\(1< \sqrt{x}< 2\)
=>1<x<4
Đúng 0
Bình luận (0)
1.cho x,y,z thuộc R thỏa mãn x+y+z+xy+xz+yz=6. Tìm GTNN của : x^2+y^2+z^2
2. cho x,y>0 thỏa mãn x+1/y<=1. tìm GTNN: A=x/y+y/x
tìm x;y thuộc z thỏa mãn x^2 + 2xy + 7(x+y) + 2y^2 + 10 = 0
Xem chi tiết
https://hoc24.vn/cau-hoi/tim-xy-thuoc-z-thoa-man-x2-2xy-7x-y-2y2-10-0.216670050813
Đúng 0
Bình luận (0)
Tìm các số x,y thuộc Z thỏa mãn:
\(2x^2+2xy-x-y-3=0\)
2x2+2xy-x-y-3=0
suy ra (2x2+2xy)-(x+y)=3
suy ra 2x(x+y)-(x+y)=3
suy ra (x+y) .(2x-1) =3
vì x, y nguyên nên x+y nguyên, 2x-1 nguyên
x+y, 2x-1 thuộc ước nguyên của 3
ta có bảng sau
| 2x-1 | 1 | -1 | 3 | -3 |
| x+y | 3 | -3 | 1 | -1 |
| x | 1 | 0 | 2 | -1 |
| y | 2 | -3 | -1 | 0 |
Vậy (x,y) thuộc { (1;2); (0;-3); (2;-1); (-1;0)}
tìm các cặp x,y thuộc z thỏa mãn
xy+x-y=0
X THOẢN MÃN VỚI DIEUEDF KIỆN X=0 VÀ Y=0
Đúng 0
Bình luận (0)
Cho /x/+/x+1/+/x+2/+/x+3/=6x
a) Chứng minh x lớn hơn hoặc bằng 0
b)Tìm x thuộc Z thỏa mãn đẳng thức trên.
a, Với mọi x, ta có: /x/; /x + 1/; /x + 2/; /x + 3/ > 0 => 6x > 0
=> x > 0 (Vì nếu x < 0 thì 6x âm và bé hơn 0)
b, Vì x > 0 => x + 1; x + 2; x + 3 > 0
=> /x/ = x
và /x + 1/ = x + 1
và /x + 2/ = x + 2
và /x + 3/ = x + 3
Ta có:
x + x + 1 + x + 2 + x + 3 = 6x
=> 4x + 6 = 6x
=> 2x = 6
=> x = 3
Đúng 0
Bình luận (0)
















