cho hình vuông abcd có diện tích là 960m2 . trên ab lấy m làm trung điểm . trên bc lấy n sao cho bn =2/3 bc.
a tính diện tich tam giác mnd
b nối AN cắt MD tại I . so sánh cạnh AI với MI .
Cho tam giác ABC có diện tích 20cm2 . trên cạnh AB lấy điểm M sao cho MA=MB, trên cạnh AC lấy điểm N sao cho AN=2NC . Nối BN và CM cắt nhau tại I a) Tính diện tích tam giác AMC . b) so sánh diện tích 2 tam giác AIC và BIC . c) AI kéo dài cắt BC tại P. So sánh BP và PC
Bài 1 : Cho tam giác ABC . Gọi D , E lần lượt là các điểm thuộc cạnh AC và AB sao cho DA = DC và EA =EB . Nối BD và CE cắt nhau tại K Biết CE = 21 cm . tính độ dài đoạn CK và KE .
Bài 2 : Cho hình vuông ABCD có cạnh 6 cm . Trên đoạn BD lấy điểm E và P sao cho BE = EP = PD .
a) Tính diện hình vuông ABCD
b) Tính diện tích hình AECP
c) M là điểm chính giữa cạnh PC , N là điểm chính giữa cạnh DC . MD và NP cắt nhau tại I . So sánh diện tích tam giác IPM với diện tích tam giác IDN
Bài 3 : Cho hình thang ABCD có đáy AB bằng 2/3 đáy CD . Trên cạnh BC lấy một điểm E sao cho đoạn BE bằng 2/5 đoạn CE . Biết diện tích tam giác AED là 32 cm2 . Tính diện tích hình thang ABCD .
Bài 4 : Cho tam giác vuông ABC có góc vuông tại A . Cạnh AB dài 3 cm , cạnh AC dài 4 cm , cạnh BC dài 5 cm . Trên cạnh AB lấy điểm M sao cho AM bằng 2 cm , trên cạnh AC lấy điểm N sao cho AN bằng 1 cm , trên cạnh BC lấy điểm E sao cho BE bằng 2,5 cm . Tính diện tích tam giác MNE
bài 1: ta có;CE là trung tuyến của tam giác ABC =>KE=1/3 CE=1/3 x21=7(cm)
CK=2/3 CE=2/3x21=14(cm0
5 người đầu tiên mình sẽ được mình tích
Cho hình tam giác ABCD . Trên cạnh AB lấy điểm M sao cho AM bằng 1/3 AB . Trên cạnh AC lấy điểm N sao cho AN bằng 1/3 AC . Nối B với N , Nói C với M ; BN cắt CM tại I
A/ So sánh diện tích Tam giác ABN với diện tích Tam giác ACM
B/ So sánh diện tích Tam giác BMI với diện tích Tam giác CNI
C/ Tính diện tích Tam giác ABC , biết Diện tích tứ giác AMIN bang 90cm2
Cho hình thang vuông ABCD , AD= 6cm ; DC = 12cm ; AB = 2/3 DC.
a) Tính diện tích hình thang ABCD.
b) Kéo dài cạnh bên AD và CB, chúng gặp nhau tại M . Tính độ dài cạnh AM.
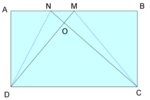
Cho hình chữ nhật ABCD có diện tích 360cm2. Trên cạnh AB lấy 2 điểm M và N sao cho AM=1/2AB, AN=1/3AB. Gọi giao điểm của DM và CN là O. Tính diện tích tam giác MON.
Cho hình chữ nhật ABCD, trên cạnh BC lấy điểm M sao cho BM = MC, trên cạnh CD lấy N sao cho NC = 1/3xDC. Hãy so sánh diện tích hình tam giác AMN với diện tích hình tam giác ADN
HCN có diện tích 360 cm2.Tính diện tích HCN với số đo chiều dài và chiều rộng tương ứng là 3/2số đo HCN đã cho
Cho hình tam giác ABC. Trên AB lấy điểm M sao cho AM = 1/3 AB. Trên AC lấy điểm N sao cho AN = 1/4 AC. Nối M với C, nối N với B cắt nhau tại O. Hãy so sánh diện tích tam giác BOC và diện tich tam giác ABC.
1)
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2)
Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2
3)
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2)

Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2
3)
AB=a ; BC=b
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2.
Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2)
3.
AB=a ; BC=b
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
cho tam giác ABC . trên cạnh BC lấy điểm I,sao cho IB=IC .Nối AI, trên đoạn AI lấy điểm M để có MI=1/2AM . Nối và kéo dài đoạn CM cắt cạnh AB tại N . so sánh diện tích hai hình tam giác AMN và BMN
Cho hình vuông ABCD cạnh bằng 8,1 cm. Trên AB lấy điểm M , sao cho AM=1/3 AB . Trên BC lấy điểm N , sao BN =2/3 BC.
a) Tính diện tích tam giác DMN b) MN va BD cắt nhau tại E . So sánh độ dài hai đoạn thẳng EM và EN
a: \(S_{AMD}=\dfrac{1}{2}\cdot8,1\cdot2,7=10,935\left(cm^2\right)\)
\(S_{BMN}=\dfrac{1}{2}\cdot5,4\cdot5,4=14,58\left(cm^2\right)\)
\(S_{NCD}=\dfrac{1}{2}\cdot8,1\cdot2,7=10,935\left(cm^2\right)\)
S ABCD=8,1^2=65,61cm2
=> S DMN=65,61-10,935*2-14,58=29,16cm2
b: Xét ΔBAC có BM/BA=BN/BC
nên MN//AC
=>MN vuông góc BD
ΔBMN cân tại B
mà BElà đường cao
nên E là trung điểm của MN
=>EM=EN
Cho tam giác ABC có diện tích là 480cm2 trên cạnh AB lấy M sao cho AM = MB , trên cạnh BC lấy N sao cho BN = 1/3 BC . Nối AN và CM cắt nhau tại I . so sánh AI và IN
cho tam giác abc , trên cạnh AB lấy điểm m sao cho AM=1/3 AB. trên cạnh AC lấy điểm N sao cho AN = 1/3AC , nối B với N , nối C vớiM ,BN cắt CM tại I
so sánh diện tích tam giác abn với diện tích tam giác ACM
b SO sánh diện tích tam gics BMI với diện tích tam giác CNI
tính diện tích tam giác ABC
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
cho hình tam giác ABC, trên cạnh BC lấy điểm I sao cho IB IC. nối AI, trên đoạn AI lấy điểm m để có MI 1 2AM. Nối và kéo dài đoạn CM cắt cạnh AB tại N. So sánh diện tích hai hình tam giác AMN và BMN ai nhanh nhất mình tick cho