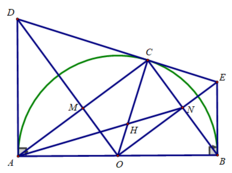
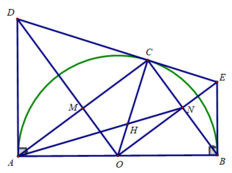
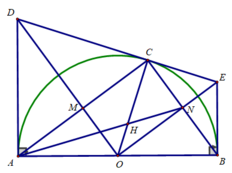
Cho nửa đường tròn (O,R), đường kính AB. Vẽ tiếp tuyến, trên Ax lấy D; trên (O) lấy E sao cho AD=DE.
a) Chứng minh DE là tiếp tuyến (O)
b) Kẻ By vuông góc AB tại B, DE cắt By tại H
Tính góc DOH
c) Chứng minh AD.BH không đổi khi E di chuyển trên (O)
d) AE cắt DO tại M; BE cắt OH tại N.
MENO là hình gì? vì sao?
e) Chứng minh AB là tiếp tuyến của đường tròn có đường kính DH.
Giúp mình với mai mình thi học kì rồi :(((((