hình chữ nhật ABCD có AB=6cm BC=4cm. có ......hinh tam giác co chieu cao =4cm
helpppppppppppp
vKhoanh vào chữ cái trước câu trả lời đúng:
Hình chữ nhật ABCD có AB = 6cm, BC = 4cm.
Trong hình vẽ bên có mấy hình tam giác có
chiều cao bằng 4cm?
A. 2 hình B. 3 hình
C. 4 hình D. 5 hình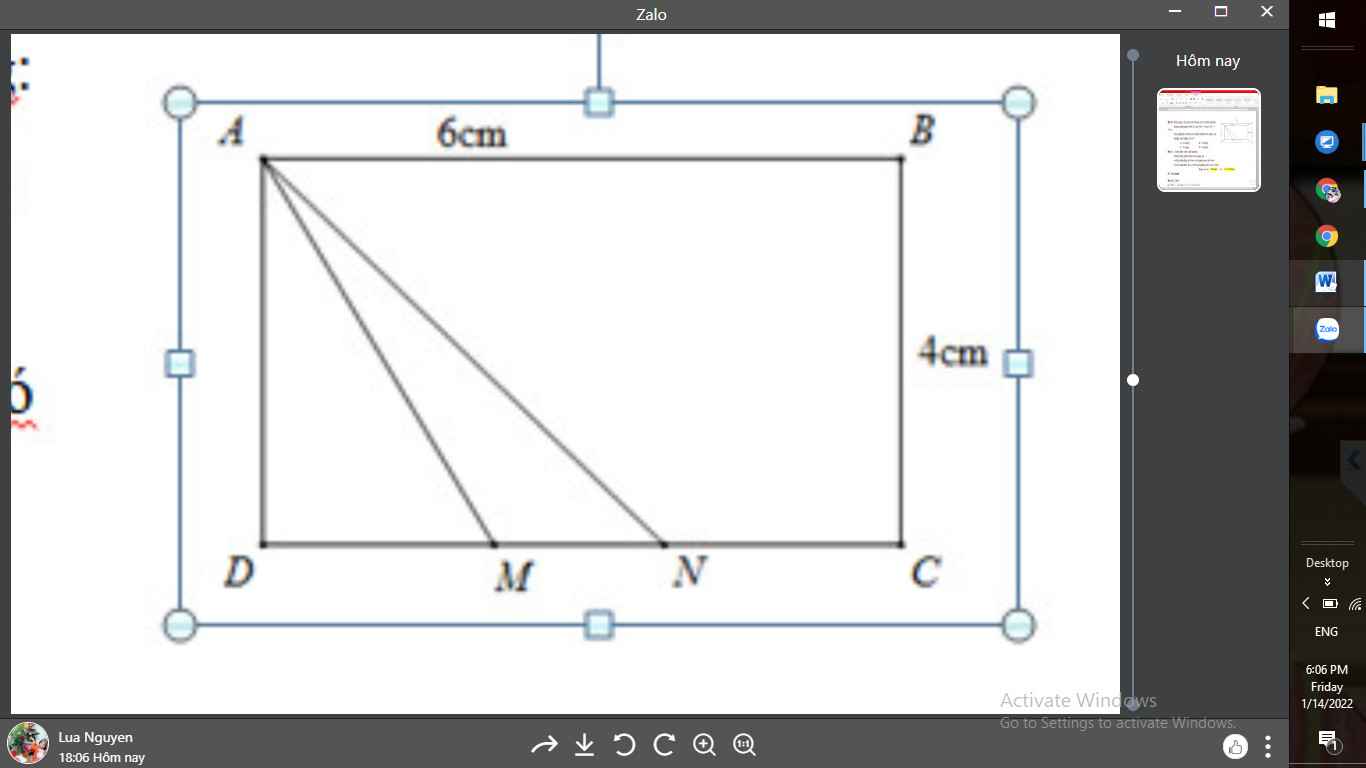
1. Tính diện tích hình tam giác vuông góc tại A, biết AB = 3cm, AC = 4cm
2. Cho hình chữ nhật ABCD có AB = 4cm, BC 3cm. Trên AB lấy điểm E sao cho AE = 1,5cm. Tính :
a) Diện tích tam giác EDC.
b) Tổng diện tích các hình tam giác AED và EBC.
3. Cho hình chữ nhật ABCD có AB = 6cm và BC = 4cm. Trên BC lấy trung điểm M, trên DC lấy trung điểm N. Tính diện tích hình tam giác AMN.
các bạn giúp mình giải với mình cảm ơn nhiều
3) Ta có: Trung điểm ở giữa đoạn thẳng
Vậy chiều cao tam giác NMC là :
4:2=2 (cm)
Đáy tam giác NMC tương tự như trên
Đáy NMC bằng 1 nữa đoạn thẳng AB
6:2=3(cm)
Diện tích tam giác NMC :
3x2:2=3(cm2)
Đoạn AB cũng là đáy cũng là đáy tam giác ABM
Vậy đáy tam giác ABM là 6cm
Chiều cao tam giác ABM bằng 1 nữa đoạn BC (tính chiều cao tgiác NMC ta dc 2cm,vì trung điểm ở giữa 2 đoạn BC
Chiều cao tam giác ABM là :
4-2=2(cm)
Diện tích tam giác ABM là :
6x2:2=6(cm2)
Chiều cao tam giác DAN=chiều rộng hcn ABCD nên chiều cao là: 4cm
Đáy tam giác DAN bằng chiều dài hcn ABCD
Đáy dài:
6:2=3(cm)
Diện tích tam giác DAN :
4x3:2=6(cm2)
Diện tích hcn ABCD :
6x4=24(cm2)
Diện tích tam giác AMN :
24-6-2-6=10(cm2)
Đs:...
1. Tính diện tích hình tam giác vuông góc tại A, biết AB = 3cm, AC = 4cm
2. Cho hình chữ nhật ABCD có AB = 4cm, BC 3cm. Trên AB lấy điểm E sao cho AE = 1,5cm. Tính :
a) Diện tích tam giác EDC.
b) Tổng diện tích các hình tam giác AED và EBC.
3. Cho hình chữ nhật ABCD có AB = 6cm và BC = 4cm. Trên BC lấy trung điểm M, trên DC lấy trung điểm N. Tính diện tích hình tam giác AMN.
các bạn giúp mình giải với mình cảm ơn nhiều
1) \(S_{ABC}=\frac{AB.AC}{2}=\frac{3\times4}{2}=6\left(cm^2\right)\)
2) a) \(S_{EDC}=\frac{AD\times DC}{2}=\frac{3\times4}{2}=6\left(cm^2\right)\) (vì chiều cao hạ từ E xuống DC = chiều rộng của hình chữ nhật)
b) \(S_{AED}+S_{EBC}=\frac{AE\times AD}{2}+\frac{EB\times BC}{2}\)
\(=\frac{AE\times AD+EB\times AD}{2}\) (vì BC = AD)
\(=\frac{AD\times\left(AE+EB\right)}{2}=\frac{3\times4}{2}=6\left(cm^2\right)\)
cho hình chữ nhật ABCD có AB=6cm và BC =4cm. trên Bc lấy trung điểm là M, DC lấy N làm trung điểm. tính diện tích tam giác AMN
Giải
Trung điểm là ở giữa hai đoạn thẳng nên chiều cao tam giác NMC là 4 : 2 = 2 (cm)
Đáy tam giác NMC cũng tương tự như vậy. Đáy NMC bằng một nửa đoạn AB nên : 6 : 2 = 3 (cm)
Diện tích tam giác NMC là: 3 x 2 :2 = 3 (cm2)
Đoạn AB cũng chính là đáy tam giác ABM nên đáy tam giác ABM là: 6 cm
Chiều cao của tam giác ABM bằng một nửa đoạn BC vì khi tính chiều cao tam giác NMC ta được 2 cm và vì trung điểm là ở giữa hai đoạn BC nên Chiều cao tam giác ABM là : 4 - 2 = 2 (cm)
Diện tích tam giác ABM là: 6 x 2 : 2 = 6 (cm2)
Chiều cao tam giác đoạn DAN bằng chiều rộng hình chữ nhật ABCD nên chiều cao là : 4 cm
Đáy tam giác DAN bằng một nửa chiều dài hình chữ nhật ABCD nên đáy dài : 6 : 2 = 3 (cm)
Diện tích tam giác DAN là: 4 x 3 : 2 = 6 (cm2)
Diện tích hình chữ nhật ABCD là : 6 x 4 = 24 (cm2)
Diện tích tam giác AMN là : 24 - 6 - 2 - 6 = 10 (cm2)
Đáp số : 10 cm2
K lm mà đòi cóvawn:))
Bài 2: Cho tam giác ABC vuông ở A, có AB = 6cm; AC = 8cm. Vẽ đường cao AH.
a) Tính BC.
b) Chứng minh AB2 = BH.BC
c) Tính BH; HC.
Bài 3: Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Vẽ đường cao AH của tam giác ADB, (H![]() BD)
BD)
a) Chứng minh DAHB ![]() DBCD.
DBCD.
b) Chứng minh AD2 = HD.DB.
c) Tính độ dài đoạn thẳng DH.
cíu oi, cíu đi gòi cho bắt zề nui, đi mà, cíuuuuuuuuuu ;-;
thui hong cần nữa, hong cíu thì thui tui tự làm liu liu 
cho hình chữ nhật ABCD có AB=8cm; BC=6cm. vẽ đường cao AH của tam giác ABD hãy chứng minh tam giác AHD đồng dạng với tam giác BAD
Xét ΔAHD vuông tại H và ΔBAD vuông tại A có
góc ADH chung
=>ΔAHD đồng dạng với ΔBAD
cho hình chữ nhật ABCD có chiều dai bang 24 cm chieu rong bang 2/3 chieu dai
a tính chu vi hình chữ nhật ABCD
b goi M là diểm chính giũa cạnh DC nối A vói M , A với C .trong hinh ve co mấy hình tam giác ?
tính diện tích hình tam giác MAC
Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Vẽ đường cao AH của tam giác ADB
a. Chứng minh tam giác AHB tam giác BCD
b. Chứng minh AD2= HD.DB
c. Tính độ dài đoạn thẳng DH
a, Xét ΔHAB và ΔCBD có :
\(\widehat{H}=\widehat{C}=90^0\)
\(\widehat{ABH}=\widehat{BDC}\left(AB//CD;slt\right)\)
\(\Rightarrow\Delta HAB\sim\Delta CBD\left(g-g\right)\)
b, Xét ΔHDA và ΔADB có :
\(\widehat{H}=\widehat{A}=90^0\)
\(\widehat{D}:chung\)
\(\Rightarrow\Delta HDA\sim\Delta ADB\left(g-g\right)\)
\(\Rightarrow\dfrac{AD}{BD}=\dfrac{HD}{AD}\)
\(\Rightarrow AD^2=HD.BD\)
c, Xét tam giác ABD vuông A theo định lý Pi-ta-go ta được :
\(\Rightarrow BD=\sqrt{AB^2+AD^2}=\sqrt{8^2+6^2}=10\left(cm\right)\)
Ta có \(\dfrac{AD}{BD}=\dfrac{HD}{AD}\left(cmt\right)\)
hay \(\dfrac{8}{10}=\dfrac{HD}{8}\)
\(\Rightarrow DH=\dfrac{8.8}{10}=6,4\left(cm\right)\)
một hinh tam giác có cạnh đáy bằng chiều dài hình chữ nhật chieu cao bằng 1/2 chieu rong hinh chữ nhật hoi dien tich hinh tam giác bang bao nhieu phan tram dien tich hinh chu nhat
S(tam giác) = (đáy x cao) : 2 = (dài x rộng) : 2
S(chữ nhật) = dài x rộng
Diện h hình tam giác bằng 1/2 diện tích hình chữ nhật
1/2 = 50%
S(tam giác) = (đáy x cao) : 2 = (dài x 1/2 rộng) : 2 = 1/4 S(chữ nhật)
DT tam giác = 1/4 DT hình chữ nhật
1/4 = 25%