Giúppp emm vớiiii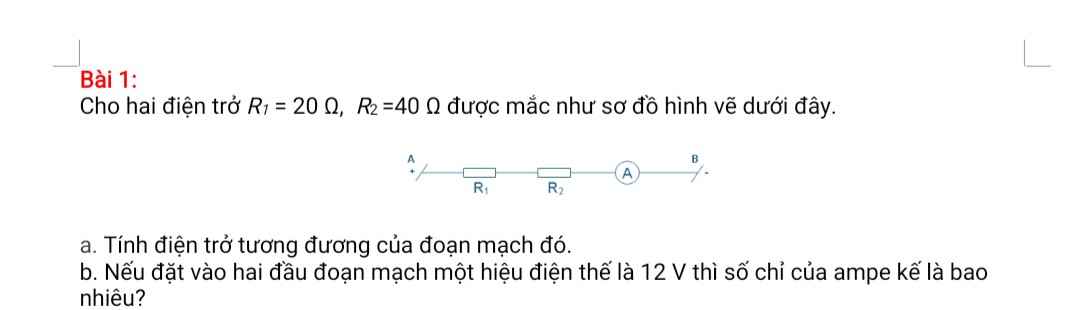

Những câu hỏi liên quan

Các cao nhân giỏi toán giúp emm với,emm đg cần gấp
Hứa tick cho các cao nhân
Mauuu giúp mk vớiiii
Giúppp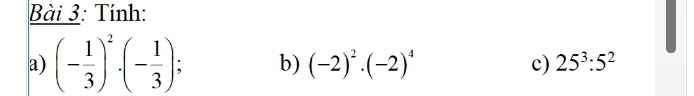
\(a,=\left(-\dfrac{1}{3}\right)^3=-\dfrac{1}{27}\\ b,=\left(-2\right)^6=2^6=64\\ c,=5^6:5^2=5^4=625\)
Đúng 2
Bình luận (2)
\(a,\left(-\dfrac{1}{3}\right)^2.\left(-\dfrac{1}{3}\right)=-\dfrac{1}{3}\)
\(b,\left(-2\right)^2.\left(-2\right)^4=\left(-2\right)^6\)
\(c,25^3:5^2=5^6:5^2=5^3\)
Đúng 1
Bình luận (0)
a.(-1/3)^2.(-1/3)=(-1/3)^3
b.(-2)^2.(-2)^4=(-2)^6
c.25^3:5^2=5^6:5^2=5^4
ht
Đúng 1
Bình luận (0)
 giúppp
giúppp
\(\dfrac{4}{5}\) x ( \(\dfrac{5}{6}\) + \(\dfrac{1}{6}\))
\(\dfrac{4}{5}\) x 1
\(\dfrac{4}{5}\)
Đúng 2
Bình luận (0)
 Giúppp
Giúppp
\(a,\dfrac{-4}{5}+\dfrac{2}{7}-\dfrac{1}{5}-\dfrac{9}{7}=\left(\dfrac{-4}{5}-\dfrac{1}{5}\right)+\left(\dfrac{2}{7}-\dfrac{9}{7}\right)=-1+\left(-1\right)=-2\)
\(b,\dfrac{1}{12}-\left(\dfrac{1}{2}+\dfrac{7}{12}\right)=\dfrac{1}{12}-\left(\dfrac{6}{12}+\dfrac{7}{12}\right)=\dfrac{1}{12}-\dfrac{13}{12}=\dfrac{-12}{12}=-1\)
\(c,\dfrac{-12}{5}-\left(\dfrac{3}{5}-\dfrac{1}{8}\right)=\dfrac{-12}{5}-\left(\dfrac{24}{40}-\dfrac{5}{40}\right)=\dfrac{-12}{5}-\dfrac{19}{40}=\dfrac{-96}{40}-\dfrac{16}{40}=\dfrac{-100}{40}=\dfrac{-5}{2}\)
\(d,\dfrac{-5}{7}-\left(\dfrac{-7}{6}+\dfrac{2}{7}\right)+\dfrac{7}{-6}=\dfrac{-5}{7}+\dfrac{7}{6}-\dfrac{2}{7}+\dfrac{-7}{6}=\left(\dfrac{-5}{7}-\dfrac{2}{7}\right)+\left(\dfrac{7}{6}+\dfrac{-7}{6}\right)=-1\)
\(e,\dfrac{-6}{5}-\dfrac{2}{7}+\dfrac{1}{5}-\dfrac{5}{7}=\left(\dfrac{-6}{5}+\dfrac{1}{5}\right)+\left(\dfrac{-2}{7}-\dfrac{5}{7}\right)=-1+\left(-1\right)=-2\)
Đúng 3
Bình luận (1)
\(a,-\dfrac{4}{5}+\dfrac{2}{7}-\dfrac{1}{5}-\dfrac{9}{7}\)
\(=\dfrac{2}{7}-\dfrac{9}{7}-\dfrac{4}{5}-\dfrac{1}{5}\)
\(=-\dfrac{7}{7}-\dfrac{5}{5}\)
\(=-1-1=-2\)
\(b,\dfrac{1}{12}-\left(\dfrac{1}{2}+\dfrac{7}{12}\right)\)
\(=\dfrac{1}{12}-\dfrac{7}{12}-\dfrac{1}{2}\)
\(=-\dfrac{6}{12}-\dfrac{1}{2}=-1\)
\(c,-\dfrac{12}{5}-\left(\dfrac{3}{5}-\dfrac{1}{8}\right)\)
\(=-\dfrac{12}{5}-\dfrac{3}{5}+\dfrac{1}{8}\)
\(=-\dfrac{15}{5}+\dfrac{1}{8}\)
\(=-3+\dfrac{1}{8}=-\dfrac{23}{8}\)
\(d,-\dfrac{5}{7}-\left(-\dfrac{7}{6}+\dfrac{2}{7}\right)+\dfrac{7}{-6}\)
=\(-\dfrac{5}{7}+\dfrac{7}{6}-\dfrac{2}{7}-\dfrac{7}{6}\)
\(=-\dfrac{5}{7}-\dfrac{2}{7}\)
\(=-\dfrac{7}{7}=-1\)
\(e.-\dfrac{6}{5}-\dfrac{2}{7}+\dfrac{1}{5}-\dfrac{5}{7}\)
\(=-\dfrac{6}{5}+\dfrac{1}{5}-\dfrac{2}{7}-\dfrac{5}{7}\)
\(=\dfrac{5}{5}-\dfrac{7}{7}\)
\(=1-1=0\)
Đúng 1
Bình luận (3)
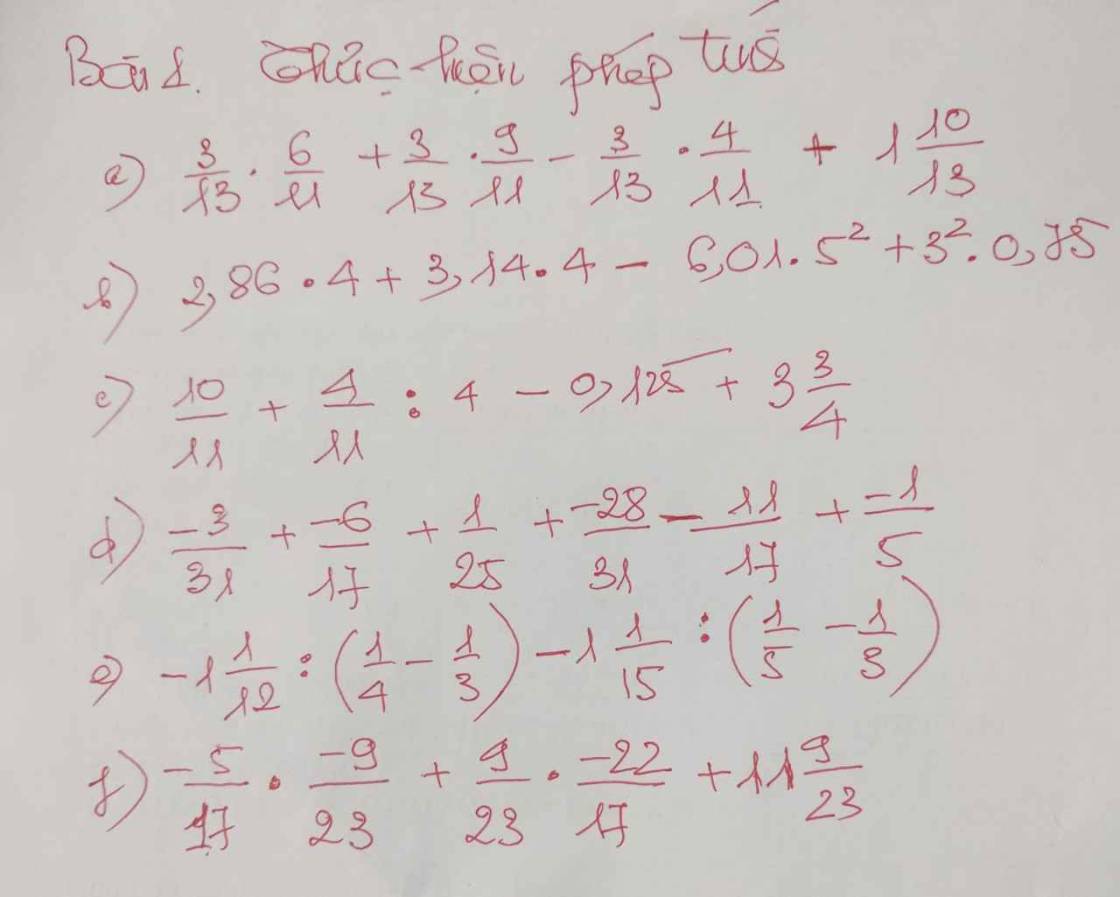 Giúppp
Giúppp
a: \(=\dfrac{3}{13}\left(\dfrac{6}{11}+\dfrac{9}{11}-\dfrac{4}{11}\right)+1+\dfrac{10}{13}=\dfrac{3}{13}+\dfrac{10}{13}+1=2\)
b: \(=4\left(2.86+3.14\right)-25\cdot6.01+9\cdot0.75\)
=4*6-25*6,01+9*0,75
=-119,5
c: \(=\dfrac{10}{11}+\dfrac{1}{11}-\dfrac{1}{8}+\dfrac{15}{4}=\dfrac{7}{8}+\dfrac{15}{4}=\dfrac{7+30}{8}=\dfrac{37}{8}\)
d: \(=\dfrac{-3}{31}-\dfrac{28}{31}-\dfrac{6}{17}-\dfrac{11}{17}+\dfrac{1}{25}-\dfrac{5}{25}=\dfrac{-4}{25}-2=-\dfrac{54}{25}\)
Đúng 0
Bình luận (0)
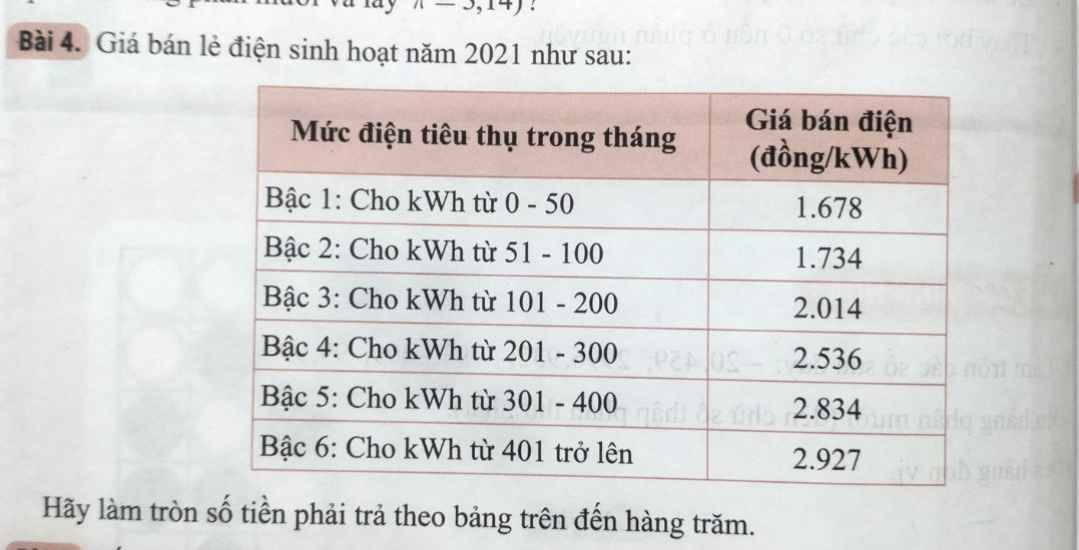 Giúppp
Giúppp
 Giúppp={{{
Giúppp={{{
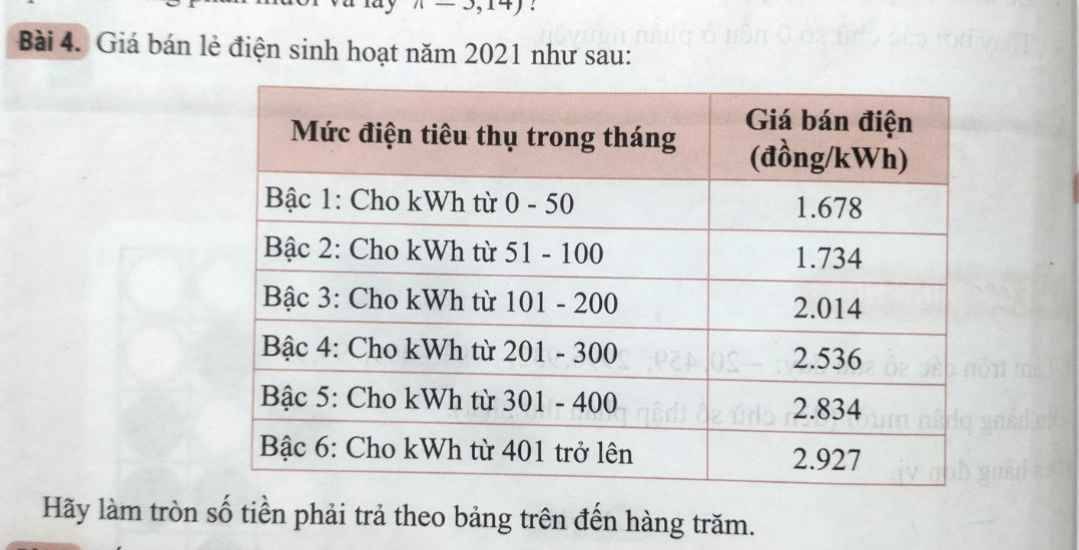
\(1.678\simeq1.68;1.734\simeq1.73\)
\(2.014\simeq2.01;2.536\simeq2.54\)
\(2.834\simeq2.83;2.927\simeq2.93\)
Đúng 0
Bình luận (0)
 Giúppp
Giúppp
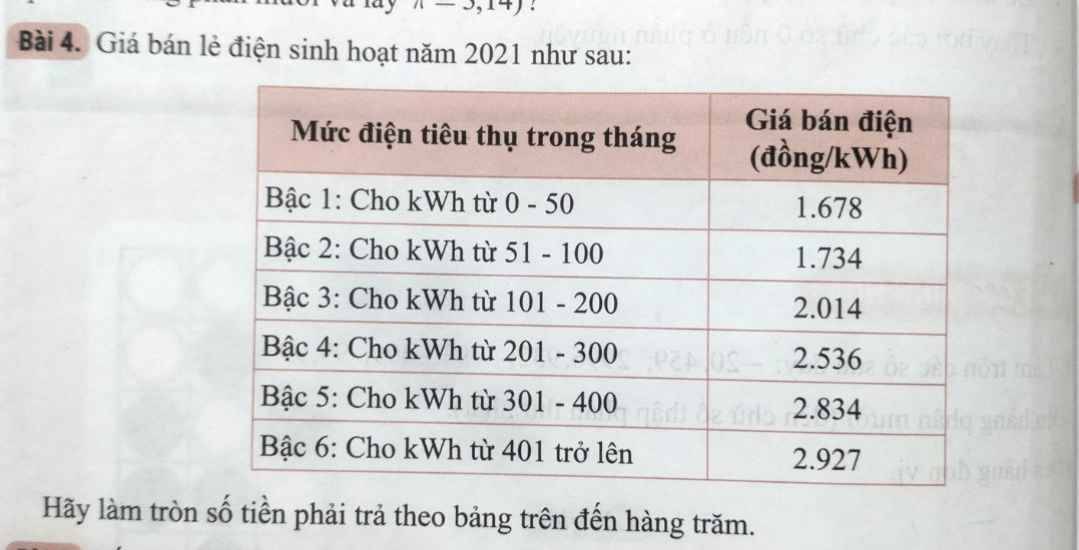
đề bài ko có số điện tiêu thụ thì làm sao tính đc ơi
Đúng 0
Bình luận (0)
 giúppp mình vs m.n
giúppp mình vs m.n
Bài 1:
a) \(\dfrac{5x-6}{2x-1}=\dfrac{3x}{x-2}\) (1)
ĐK:\(\left\{{}\begin{matrix}2x-1\ne0\\x-2\ne0\end{matrix}\right.\) ⇔\(\left\{{}\begin{matrix}x\ne\dfrac{1}{2}\\x\ne2\end{matrix}\right.\)
(1) ⇒\(\dfrac{\left(5x-6\right)\left(x-2\right)}{\left(2x-1\right)\left(x-2\right)}=\dfrac{3x\left(2x-1\right)}{\left(2x-1\right)\left(x-2\right)}\)
⇔\(5x^2-10x-6x+12=6x^2-3x\)
⇔\(5x^2-10x-6x+12-6x^2+3x=0\)
⇔\(-x^2-13+12=0\)
⇔\(\left[{}\begin{matrix}x=\dfrac{-13+\sqrt{217}}{2}\\x=\dfrac{-13-\sqrt{217}}{2}\end{matrix}\right.\left(TM\right)\)
KL:
Đúng 0
Bình luận (0)
Bạn nên đăng vào lớp 9 để nhận được nhiều sự trợ giúp hơn nhé !
Đúng 0
Bình luận (0)
Bài 1: b) \(\dfrac{7x}{2x+2}=\dfrac{3x+1}{x-5}\) (2)
ĐK: \(\left\{{}\begin{matrix}2x+2\ne0\\x-5\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\x\ne5\end{matrix}\right.\)
(2)⇒ \(\dfrac{7x\left(x-5\right)}{\left(2x+2\right)\left(x-5\right)}=\dfrac{\left(3x+1\right)\left(2x+2\right)}{\left(2x+2\right)\left(x-5\right)}\)
\(\Leftrightarrow7x^2-35x=6x^2+6x+2x+2\)
\(\Leftrightarrow7x^2-35x-6x^2-6x-2x-2=0\)
\(\Leftrightarrow x^2+27x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-27+\sqrt{737}}{2}\\x=\dfrac{-27+\sqrt{737}}{2}\end{matrix}\right.\left(TM\right)\)
KL:
Đúng 0
Bình luận (0)



























