a) Vẽ đồ thị (P) của hàm số y = x² - 4x + 3
b) Dựa vào đồ thị, tìm m để phương trình sau có nghiệm: x² - 4x + 3 = 0
a, Lập bảng biến thiên, vẽ đồ thị (P) của hàm số : y = - x^2 + 4x - 3
b, Dựa vào đồ thị, hãy:
+ Tìm x để y > 0 ; y < 0;
+ Tìm max, min của hàm số trên đoạn [0;4].
+ Biện luận theo m số nghiệm của pt x^2 - 4x = m
+Tìm k để pt -x^2 + 4x = k có nghiệm thỏa mãn [-1;3]
a: Vì a=-1<0 nên hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (-∞;2]
Bảng biến thiên là:
| x | -∞ | 2 | +∞ |
| y | -∞ | 1 | -∞ |
cho hàm sô y= x2 -4x+3(P)
a, vẽ đồ thị (P') và lập bảng biến thiên của y= | -x2 +4x-3|
b, dựa vào đồ thị (P') , biện luận theo m số nghiệm phương trình | x2-4x+3|-m-1=0
Cho hàm số y=f(x) có đạo hàm trên ℝ . Đồ thị hàm số y=f'(x) như hình vẽ bên dưới
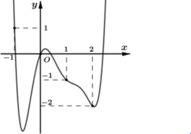
Tìm m để bất phương trình m - x ≥ 2 f x + 2 + 4 x + 3 nghiệm đúng với mọi x ∈ - 3 ; + ∞
A. m ≥ 2 f ( 0 ) - 1
B. m ≤ 2 f ( 0 ) - 1
C. m ≤ 2 f ( - 1 )
D. m ≥ 2 f ( - 1 )
Đáp án B
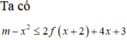
![]()
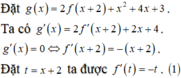
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
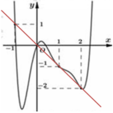
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có



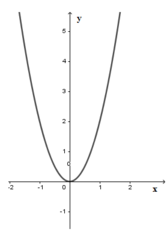
Cho đồ thị hàm số y = 2 x 2 (P) như hình vẽ. Dựa vào đồ thị, tìm m để phương trình 2 x 2 – m – 5 = 0 có hai nghiệm phân biệt.
A. m < −5
B. m > 0
C. m < 0
D. m > −5
Ta có 2x2 – m – 5 = 0 (*)
⇔ 2x2 = m + 5
Số nghiệm của phương trình (*) là số giao điểm của
parabol (P): y = 2x2và đường thẳng d: y = m + 5
Để (*) có hai nghiệm phân biệt thì d cắt (P) tại
hai điểm phân biệt.Từ đồ thị hàm số ta thấy:
Với m + 5 > 0 ⇔ m > −5 thì d cắt (P)
tại hai điểm phân biệt hay phương trình (*)
có hai nghiệm phân biệt khi m > −5
Đáp án cần chọn là: D
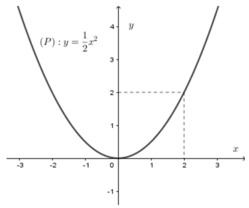
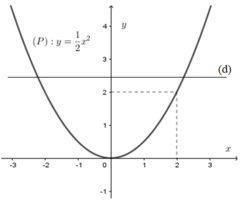
Cho đồ thị hàm số y = 1 2 x 2 (P) như hình vẽ. Dựa vào đồ thị, tìm m để phương trình x 2 – 2 m + 4 = 0 có hai nghiệm phân biệt
A. m > 2
B. m > 0
C. m < 2
D. m > −2
Xét phương trình x2 – 2m + 4 = 0 (*)
⇔ x2 = 2m – 4 ⇔ 1 2 x 2 = m − 2
Số nghiệm của phương trình (*) là
số giao điểm của parabol (P): y = 1 2 x 2
và đường thẳng d: y = m – 2
Để (*) có hai nghiệm phân biệt thì d cắt (P) tại hai điểm phân biệt
Từ đồ thị hàm số ta thấy:
Với m – 2 > 0 ⇔ m > 2 thì d cắt (P)
tại hai điểm phân biệt hay phương trình (*)
có hai nghiệm phân biệt khi m > 2
Đáp án cần chọn là: A
Cho đồ thị hàm số y = x\(^2\) -2x - 3 :
Dựa vào đồ thị biện luận theo m số nghiệm của phương trình: x^2 - 2x - 3 + m = 0
Cho hàm số y = ( − 3 m + 1 ) x 2 . Tìm m để đồ thị hàm số đi qua điểm A (x; y) với (x; y) là nghiệm của hệ phương trình 4 x − 3 y = − 2 x − 2 y = − 3
A. m = 1 3
B. m = - 1 3
C. m = 3
D. m = − 3
Đồ thị hàm số y = f ( x ) = x 2 - 4 x + 3 được cho trong hình 46. Từ hình vẽ nãy hãy chỉ ra tập nghiệm của bất phương trình x 2 - 4 x + 3 > 0
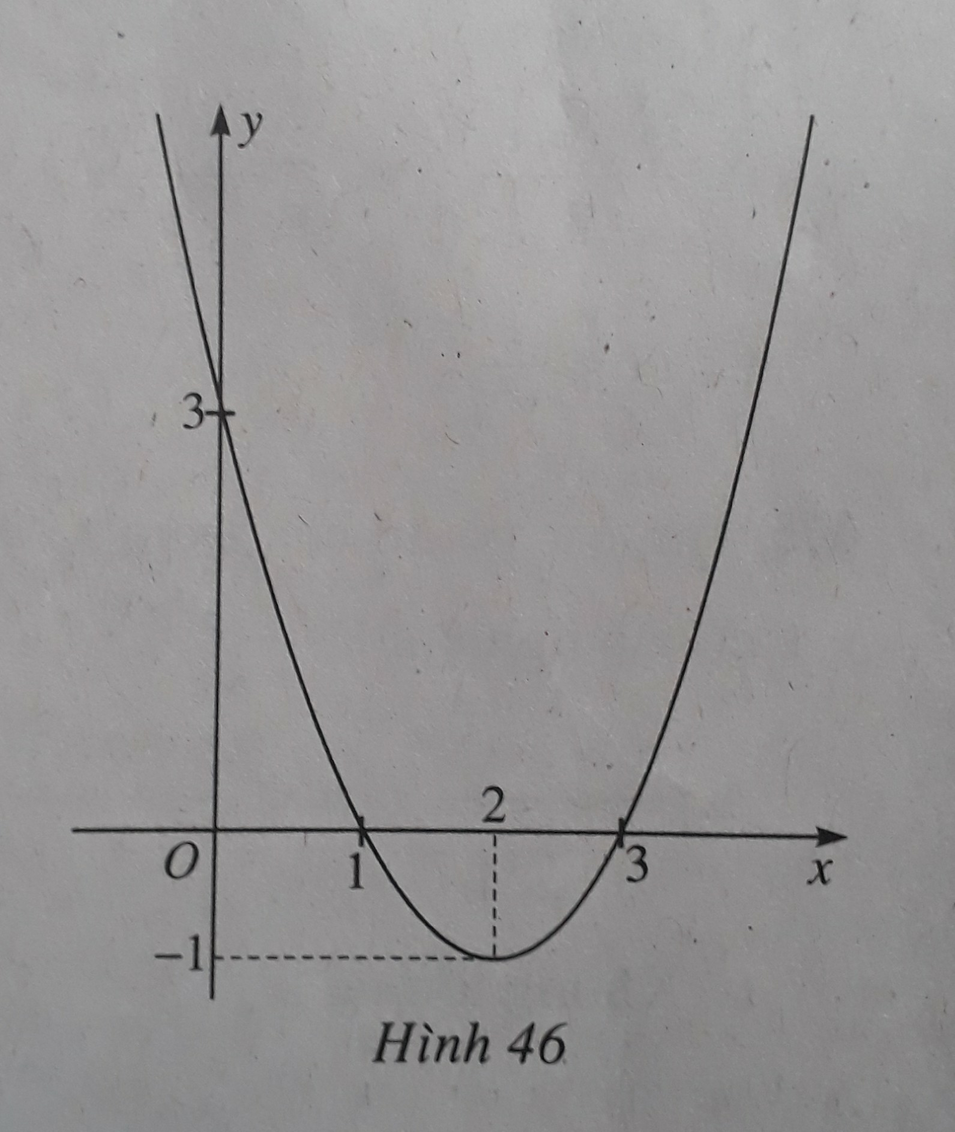
A. x < 1
B. x ≥ 1
C. 1 < x < 3
D. ( - ∞ ; 1 ) ∪ ( 3 ; + ∞ )
a, Vẽ đồ thị hàm số y= \(\sqrt{4x^2-4x+1}\) + \(\sqrt{x^{2^{ }}-4x+4}\)
b, Biện luận theo m số nghiệm của phương trình:
\(\sqrt{4x^{2^{ }}-4x+1}\)+ \(\sqrt{x^{2^{ }}-4x+4}\) = m
\(y=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(x-2\right)^2}=\left|2x-1\right|+\left|x-2\right|\)
\(y=\left[{}\begin{matrix}3x-3\left(\text{với }x\ge2\right)\\3-3x\left(\text{với }x\le\dfrac{1}{2}\right)\\x+1\left(\text{với }\dfrac{1}{2}\le x\le2\right)\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau:
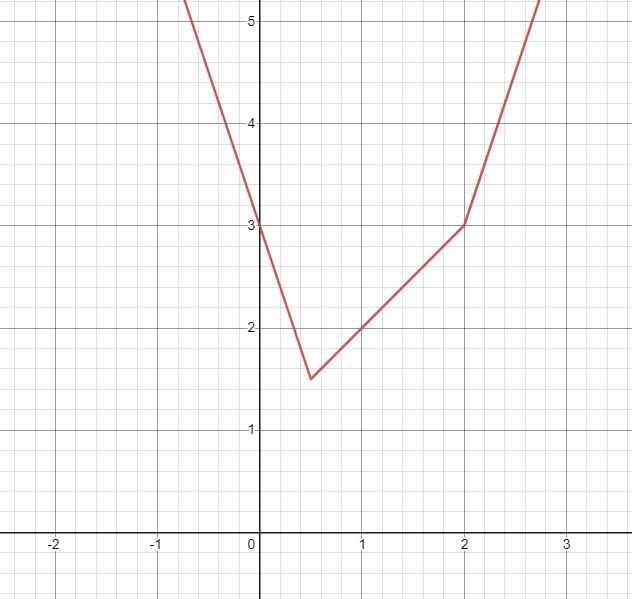
Từ đồ thị ta thấy phương trình \(\sqrt{4x^2-4x+1}+\sqrt{x^2-4x+4}=m\):
- Có đúng 1 nghiệm khi \(m=\dfrac{3}{2}\)
- Có 2 nghiệm phân biệt khi \(m>\dfrac{3}{2}\)
- Vô nghiệm khi \(m< \dfrac{3}{2}\)