cho tứ diện ABCD. Gọi G1, G2, G3 lần lượt là trọng tâm của các tam giác SAB,SDC,SBC.Gọi (a) là mặt phẳng đi qua ba điểm G1,G2,C.Tìm giao điểm K của đường thẳng SA với mặt phẳng (a)
Cho tứ diện ABCD. Lấy điểm S nằm ngoài mặt phẳng (ABCD). Gọi lần lượt G1, G2 là trọng tâm của tam giác SAB và tam giác SBD Chứng minh BD song song với mặt phẳng (SG1G2)
Cho tứ diện ABCD. Gọi G1, G2, G3 lần lượt là trọng tâm các tam giác ABC, ACD, ADB. M là điểm di động bên trong tứ diện sao cho \(G_1M\) luôn song song với mặt phẳng (ACD). Tìm tập hợp những điểm M
Cho hình chóp S.ABCD có đáy là tứ giác ABCD. Gọi G 1 và G 2 lần lượt là trọng tâm của các tam giác SBC và SCD
Tìm giao tuyến của mặt phẳng ( A G 1 G 2 ) với các mặt phẳng (ABCD) và (SCD).
Xác định thiết diện của hình chóp với mặt phẳng ( A G 1 G 2 ) .
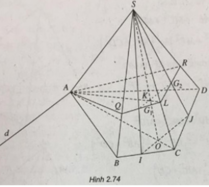
Gọi I, J lần lượt là trung điểm của BC, CD.
Ta có I J / / G 1 G 2 nên giao tuyến của hai mặt phẳng ( A G 1 G 2 ) và (ABCD) là đường thẳng d qua A và song song với IJ
Gọi O = IJ ∩ AC, K = G 1 G 2 ∩ S O , L = AK ∩ SC
L G 2 cắt SD tại R
L G 2 cắt SB tại Q
Ta có thiết diện là tứ giác AQLR.
Cho hình hộp ABCD.A’B’C’D’.
a) Chứng minh rằng hai mặt phẳng (BDA’) và (B’D’C) song song với nhau.
b) Chứng minh rằng đường chéo AC’ đi qua trọng tâm G1 và G2 lần lượt của hai tam giác BDA’ và B’D’C.
c) Chứng minh G1 và G2 chia đoạn AC’ thành ba phần bằng nhau.
d) Gọi O và I lần lượt là tâm các hình bình hành ABCD và AA’C’C. Xác định thiết diện của mặt phẳng (A’IO) với hình hộp đã cho.
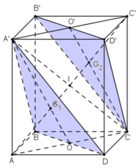
a) + A’D’ // BC và A’D’ = BC
⇒ A’D’CB là hình bình hành
⇒ A’B // D’C, mà D’C ⊂ (B’D’C) ⇒ A’B // (B’D’C) (1)
+ BB’ // DD’ và BB’ = DD’
⇒ BDD’B’ là hình bình hành
⇒ BD // B’D’, mà B’D’ ⊂ (B’D’C) ⇒ BD // (B’D’C) (2)
A’B ⊂ (BDA’) và BD ⊂ (BDA’); A’B ∩ BD = B (3)
Từ (1), (2), (3) suy ra : (BDA’) // (B’D’C).
b) Gọi O = AC ∩ BD
+ Ta có: O ∈ AC ⊂ (AA’C’C)
⇒ A’O ⊂ (AA’C’C).
Trong (AA’C’C), gọi A’O ∩ AC’ = G1.
G1 ∈ A’O ⊂ (A’BD)
⇒ G1 ∈ AC’ ∩ (BDA’).
+ Trong hình bình hành AA’C’C gọi I = A’C ∩ AC’
⇒ A’I = IC.
⇒ AI là trung tuyến của ΔA’AC
⇒ G 1 = A ’ O ∩ A C ’ là giao của hai trung tuyến AI và A’O của ΔA’AC
⇒ G 1 là trọng tâm ΔA’AC
⇒ A ’ G 1 = 2 . A ’ O / 3
⇒ G 1 cũng là trọng tâm ΔA’BD.
Vậy AC' đi qua trọng tâm G 1 của ΔA’BD.
Chứng minh tương tự đối với điểm G 2 .
c) *Vì G 1 là trọng tâm của ΔAA’C nên A G 1 / A I = 2 / 3 .
Vì I là trung điểm của AC’ nên AI = 1/2.AC’
Từ các kết quả này, ta có : A G 1 = 1 / 3 . A C ’
*Chứng minh tương tự ta có : C ’ G 2 = 1 / 3 . A C ’
Suy ra : A G 1 = G 1 G 2 = G 2 C ’ = 1 / 3 . A C ’ .
d) (A’IO) chính là mp (AA’C’C) nên thiết diện cần tìm chính là hình bình hành AA’C’C.
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là G 1 , G 2 .
Tìm câu đúng nhất.
Thiết diện của hình tứ diện cắt bởi mặt phẳng ( B G 1 G 2 ) là:
A. Tam giác
B. Tứ giác
C. Tam giác cân
D. Hình thang
Gọi I là trung điểm CD thì G 1 ∈ B I , G 2 ∈ A I ⇒ mặt phẳng ( B G 1 G 2 ) chính là mặt phẳng (ABI) ⇒ Thiết diện là tam giác cân AIB.
Đáp án C
Cho tứ diện ABCD. Gọi G 1 và G 2 lần lượt là trọng tâm của tam giác ACD và BCD. Chứng minh rằng G 1 G 2 song song với các mặt phẳng (ABC) và (ABD).
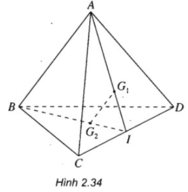
Gọi I là trung điểm của CD.
Vì G 1 là trọng tâm của tam giác ACD nên G 1 ∈ A I
Vì G 2 là trọng tâm của tam giác BCD nên G 2 ∈ B I
Ta có :
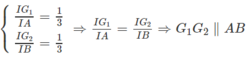
A B ⊂ ( A B C ) ⇒ G 1 G 2 / / ( A B C )
Và A B ⊂ ( A B D ) ⇒ G 1 G 2 / / ( A B D )
Cho tứ diện ABCD. Lấy G1,G2,G3
lần lượt là trọng tâm của các tam giác ABC, ACD, ADB.
a) Chứng minh rằng (G1G2G3)//(BCD)
b) Xác định giao tuyến của mặt phẳng (G1G2G3) với mặt phẳng (ABD)
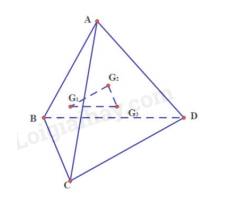
a) Gọi E, F, H là trung điểm của BC, CD, BD
Ta có:\({G_1}\) là trọng tâm tam giác ABC, suy ra\(\frac{{A{G_1}}}{{AE}} = \frac{2}{3}\)
\({G_3}\)là trọng tâm tam giác ABD, suy ra\(\frac{{A{G_3}}}{{AH}} = \frac{2}{3}\)
Suy ra tam giác AEH có\(\frac{{A{G_1}}}{{AE}} = \frac{{A{G_3}}}{{AH}}\) nên \({G_1}{G_3}//EH\)
Mà EH thuộc (BCD) nên \({G_1}{G_3}//(BCD)\)
Tương tự ta có:\({G_2}{G_3}//(BCD)\)
Do đó, \({G_1}{G_2}{G_3}//(BCD)\)
b) Ta có: \({G_1}{G_2}{G_3}//(BCD)\) nên \({G_1}{G_2} // BD\)
mà \({G_3}\) là điểm chung của hai mặt phẳng
Từ \({G_3}\) kẻ \({G_3}x\) sao cho \({G_3}x//BD\)
Vậy \({G_3}x\) là giao tuyến cần tìm.
Cho khối tứ diện ABCD có thể tích V. Gọi G 1 , G 2 , G 3 , G 4 là trọng tâm 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện G 1 , G 2 , G 3 , G 4 là
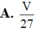
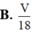
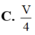
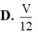
Cho khối tứ diện ABCD có thể tích V. Gọi G 1 G 2 G 3 G 4 là trọng tâm của 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện G 1 G 2 G 3 G 4 là
A. V 27
B. V 18
C. V 4
D. V 12